1588

A Novel Strategy For Morphologically Faithful Registration and Template Creation for Diffusion MRI Data

M. Okan Irfanoglu¹, Neda Sadeghi¹, Carlo Pierpaoli¹, and Moebius Syndrome Research Consortium²

¹QMI/NIBIB, National Institutes of Health, Bethesda, MD, United States, ²National Institutes of Health, Bethesda, MD, United States

Synopsis

Spatial alignment of diffusion tensor MRI (DTI) data is of fundamental importance for voxelwise statistical analysis and creation of population specific atlases of diffusion MRI metrics. Most available DTI-based spatial normalization algorithms emphasize alignment of anisotropic structures and disregard the quality of alignment for gray matter and CSF-filled regions. Additionally, standard atlas creation strategies using these registration tools do not generate templates that are morphologically representative of average features of the population. In this work, we propose a new DTI-based registration and atlas creation method that aims to overcome these challenges.

Introduction

The availability of anatomically accurate MRI atlases is essential for quantitative analysis of MRI data. Ideally, these atlases should be representative of the average features of the population at each voxel. This necessitates the use of a morphologically constrained atlas creation strategy^1,2,3 and a registration method that can provide accurate alignment in all brain regions. Historically, diffusion tensor MRI (DTI) registration methods emphasized white matter (WM) alignment, which is not ideal for whole brain studies. The recently published DTI registration tool DR-TAMAS⁴ achieves accurate alignment in also gray matter (GM) and CSF-filled regions by employing a locally varying metric that uses the Trace, deviatoric tensor and scalar image information. However, this method did not produce morphologically faithful atlases unless additional constraints were imposed, employed a small deformation model that was unable to model a mapping between significantly different images and required the entire atlas creation process to be repeated when new subjects were added to the population. In this work, we propose a new DTI registration method that aims to overcome these challenges.

Methods & Theory

The philosophy behind the atlas creation process is as follows: Avants et al. proposed the SyN⁵ transformation that can intrinsically solve the "2-image diffeomorphic averaging problem"⁵ by employing two separate deformation fields. When these fields are constrained to be inverses, this strategy also guarantees morphological shape consistency. Therefore, for a population consisting of power-of-two number of subjects, SyN can be used for recursive pairwise registration, as in a binary-tree, to create the final template. However, this strategy is not applicable to non power-of-two images. Therefore, we developed a framework that employs the large-deformation diffeomorphic metric-mapping's (LDDMM)⁶ time-varying-velocity-fields (TVVF) for geodesic interpolation⁷ for atlas creation. The velocity fields $$$v(x,t)$$$ are densely sampled on the abstract time domain ($$$t \in[0,1]$$$), constrained to be symmetric with constant speed and arc-length⁷. Let $$$A$$$ be a template computed from $$$N$$$ and $$$B$$$ from $$$K$$$ subjects, residing at $$$t=0$$$ and $$$t=1$$$ respectively. These templates can be from previous atlas creation processes or from a different level of template creation tree. The deformation fields warping $$$A$$$ and $$$B$$$ to $$$A’=A(\phi_A)$$$ and $$$B’=B(\phi_B)$$$ are then:

$$$\phi_A(x)=\int_{K/(N+K)}^0 v(x,t)dt$$$ , $$$\phi_B(x)=\int_{K/(N+K)}^1 v(x,t)dt$$$

The corresponding template is: $$$(N.A’ + K.B’) / (N+K)$$$. This logic can also be employed to update an existing atlas with new subjects.

Materials & Validation

Eight subjects of the Connectome⁸ dataset were used to create an atlas. To assess the quality of large-deformation registration, a patient suffering from congenital cranial dysinnervation disorder caused by mutations in TUBB3 was scanned on a Philips 3T system. This disorder is associated with agenesis or hypoplasia of the corpus callosum and anterior commissure. DTI data were acquired with seven low b-values and 39 volumes with a max b=1100s/mm². (TR=10.5s, TE=85ms, slices=90, voxel size=2x2x2mm). The sequence was repeated for AP and PA phase encoding directions. DWIs were corrected for motion, eddy-currents and EPI distortions⁹.

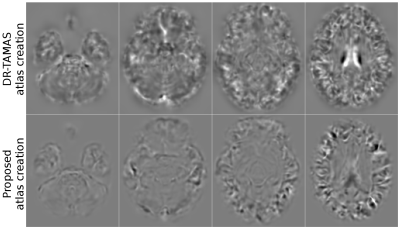
We compared the results of the new atlas creation method to the well-established Joshi method¹⁰ implemented in DR-TAMAS, to demonstrate that the two methods produce very similar atlases in the absence of large deformations, which is desirable property. The average log-Jacobians of the deformation fields were examined to determine the morphological faithfulness of the computed atlas to the average anatomy. Ideally, for the template to be a morphological average, these maps should be flat, indicating no expansions or contractions were necessary on average. The large deformation capabilities were tested by registering the TUBB3 patient to an existing template.

Results

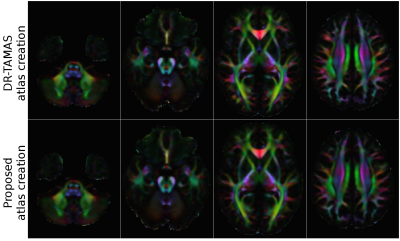
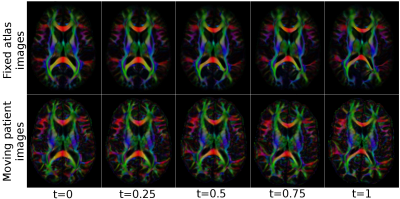
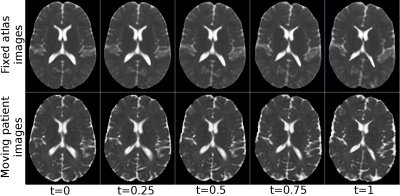
Figure 1 displays the directionally encoded color (DEC) maps of the atlases from DR-TAMAS and the proposed method. The two methods produced very similar results with this dataset, with very subtle differences. The accuracy of both registration algorithms and the atlas creation methods along with the high resolution of the Connectome data, produced very high quality atlases with exquisite anatomical details. Figure 2 displays the average log-Jacobians of the deformation fields. The proposed method generates more homogeneous maps compared to the unconstrained DR-TAMAS. Figure 3 and 4 display the results of the registration of the patient suffering from TUBB3. The large deformation diffeomorphic model was able to align both images accurately at all time points with all brain regions being in correspondence.

Conclusions & Discussion

The proposed DTI registration method shows excellent overall performance in the entire brain, including WM, GM and CSF-filled regions. The atlas creation strategy is morphologically unbiased, can accommodate large deformations and can be used to update existing templates with new subjects. These methods can also be used for registration of higher order diffusion models. For full theoretical completeness, its output can be fed to other atlas creation strategies to remove the significant impact of initial template selection/creation process.

Acknowledgements

This work was supported by the Intramural Research Programs of the National Institute of Biomedical Imaging and Bioengineering (NIBIB).

References

1. M. Okan Irfanoglu, N. Sadeghi, A. Nayak, C. Pierpaoli, “Strategies for building a morphologically faithful average brain template from population diffusion MRI data”, In Proceedings of 25th International Society for Magnetic Resonance in Medicine (ISMRM'17), Honolulu, Hawaii, 22-27 April 2017.

2. M. F. Beg and A. Khan, "Computing an average anatomical atlas using LDDMM and geodesic shooting," 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006., Arlington, VA, 2006, pp. 1116-1119.

3. B. B. Avants, P. Yushkevich, J. Pluta, D. Minkoff, M.Korczykowski, J. Detre, J. C. Gee, “The optimal template effect in hippocampus studies of diseased populations”, NeuroImage, Volume 49, Issue 3, 2010, Pages 2457-2466.

4. M. Okan Irfanoglu, A. Nayak, J. Jenkins, E. B. Hutchinson, N. Sadeghi, C. P. Thomas, C. Pierpaoli, “DR-TAMAS: Diffeomorphic Registration for Tensor Accurate Alignment of Anatomical Structures”, NeuroImage, Volume 132, 2016, Pages 439-454.

5. Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal. 2008 Feb;12(1):26–41.

6. F. Beg, M.Miller, A. Trouve, and L. Younes. “Computing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms”, International Journal of Computer Vision, Volume 61, Issue 2; February 2005.

7. B.Avants, J. C. Gee, “Geodesic estimation for large deformation anatomical shape averaging and interpolation”, NeuroImage, Volume 23, Supplement 1, 2004, Pages S139-S150.

8. D. C. Van Essen, S.M. Smith, D. M. Barch, T. E.J. Behrens, E. Yacoub, K. Ugurbil, WU-Minn HCP Consortium. (2013). “The WU-Minn Human Connectome Project: An overview”, NeuroImage 80(2013):62-79.

9. C. Pierpaoli, L. Walker, M. O. Irfanoglu, A. Barnett, P. Basser, L-C. Chang, C. Koay, S. Pajevic, G. Rohde, J. Sarlls, and M. Wu, 2010, TORTOISE: an integrated software package for processing of diffusion MRI data, ISMRM 18th annual meeting, Stockholm, Sweden

10. S. Joshi, B. Davis, M. Jomier, G. Gerig, “Unbiased diffeomorphic atlas construction for computational anatomy”, NeuroImage, Volume 23, Supplement 1, 2004, Pages S151-S160.

Figures

Figure 1. DEC maps of the templates computed from the 8 subjects of the Connectome dataset using the Joshi's atlas creation method¹⁰ implemented in DR-TAMAS⁴ and the proposed geodesic interpolation method. The two atlases are nearly identical with subtle differences, which is desirable. Anatomical detail levels for both methods is exquisite thanks to the quality of the registration and atlas creation methods and the high resolution of Connectome.

Figure 2. Log-Jacobian determinant of the average of the deformation fields mapping each subject onto the computed atlas. Bright intensities indicate that on average a voxel was reduced in size and dark intensities indicate a voxel on average was increased in size. The gray shade in the background is zero. Ideally, for the template to be a morphological average, these maps should be flat with constant zero value. The proposed method of atlas creation generates significantly more homogeneous Jacobian maps compared to the unconstrained DR-TAMAS. The window is scaled from -0.5 to 0.5.

Figure 3. DEC maps of the warped healthy atlas and the patient image. Images are visualized at different morphing timepoints. The original target image is the fixed image at t=0 (top left) and the original source image is the patient image at t=1 (bottom right). The patient brain warped to the template is at the bottom left and the template warped to patient brain is at top right. The proposed registration performs a very accurate registration in all brain regions for all time points.

Figure 4. Trace maps from the same diffeomorphic registration. The proposed registration was capable to accurately align gray matter and CSF-filled regions as well, in addition to the anisotropic regions as depicted in Figure 3.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1588