1577
Anatomical atlas of MAP MRI-derived 3D diffusion propagators and microstructural parameters1NIBIB, National Institutes of Health, Bethesda, MD, United States, 2NICHD, National Institutes of Health, Bethesda, MD, United States, 3NINDS, National Institutes of Health, Bethesda, MD, United States, 4Diagnostic Radiology, National Institutes of Health, Bethesda, MD, United States, 5National Institutes of Health, Bethesda, MD, United States
Synopsis
We describe the construction of an anatomical template of 3D probability distributions water molecule displacements in tissues (i.e., diffusion propagators) measured with MAP MRI in a population of healthy volunteers. From the template of 3D diffusion propagators, we compute normative values of MAP MRI microstructural parameters and visualize the orientational characteristics of water net displacement profiles using orientation distribution functions (ODFs). This atlas could provide a reference for protocol development in longitudinal and multi-center studies, and for clinical studies seeking to detect and characterize subtle microstructural changes, such as those occurring in mild traumatic brain injury (mTBI), or metastatic cancer.
Introduction
Anatomical brain atlases constructed from diffusion tensor imaging (DTI)1 data provide important clinical references for delineating, labeling, and characterizing brain regions. These atlases2 can uniquely differentiate anatomical regions (especially in white matter) based on structural tissue parameters such as fractional anisotropy (FA), mean diffusivity (MD), and direction-encoded color (DEC) map, which describe the underlying microstructure and cytoarchitecture.
A comprehensive quantitation of the underlying tissue microstructure can be obtained by explicitly measuring the 3D probability distribution of microscopic net displacements of diffusion water molecules in tissues, i.e., diffusion propagators, without the DTI assumption of Gaussian diffusion. Mean apparent propagator (MAP) MRI3 provides an efficient, elegant, and clinically feasible4 solution, approximating the 3D diffusion propagators and deriving a family of new microstructural parameters such as the Return-to-Origin Probability (RTOP), the Non-Gaussianity (NG), and the Propagator Anisotropy (PA), in addition to the FA, MD and DEC maps obtained from DTI. In this study, we describe our approach for constructing an atlas of 3D diffusion propagators in a population of healthy normal individuals and subsequently deriving population-averaged (i.e., normative) values of MAP MRI microstructural parameters.
Methods
Seven healthy individuals were scanned using MAP MRI and the following imaging parameters: 42 slices with 3mm slice thickness, a 21x21cm field-of-view (FOV) on an imaging matrix of 70x70 resulting in a 3mm isotropic voxel resolution. Using conventional spin-echo diffusion EPI, 498 DWIs were acquired with multiple b-values (maximum b=6000 s/mm2) and diffusion gradients applied along non-collinear orientations.
All DWI data was first processed with the TORTOISE software package5 to correct for EPI distortions and subject motion. DTI was fit to data acquired with low b-values (b<2000 s/mm2) in each subject, and subsequently processed to generate a DTI population atlas6. The inverse of the deformation field transformations from individual to template space were applied directly to transform the corrected DWIs and associated gradient vectors to the template space6 (Fig. 1). Finally, 3D propagators were computed from the transformed DWIs and voxel-wise b-matrix components (in template space) using MAP MRI with orthogonal basis functions derived from the population template DTI data (Fig 1).
By averaging the diffusion propagators of all registered subjects expressed in the same MAP MRI functional basis we computed a population template. From the template 3D diffusion propagators we derived MAP MRI microstructural parameters and visualized orientational profiles using the orientation distribution functions (ODFs).
Results
Microstructural MAP MRI parameters derived from the template 3D diffusion propagators were consistent with previous clinical measurements in healthy brain tissue4,7,8 (Fig. 2). Despite the 3mm spatial resolution, and the anatomical variations across subjects, the RTOP, PA, and NG maps showed adequate delineation of white matter (WM) and gray matter (GM) tissues. Moreover, population-averaged template 3D propagators also showed anatomical variations in orientational profiles in GM and WM regions that may be used to define and delineate brain regions for altas construction (Fig. 3).
Describing the MAP propagators of registered subjects with the same functional basis allows direct comparison and averaging of MAP MRI coefficients. Subtle differences between 3D propagators (expressed in the same MAP MRI basis) can be comprehensively quantified using a probability distance measure. Such quantitative comparison between 3D propagators may provide a sensitive method for detecting subtle tissue changes in pathologies with diffuse presentations, particularly in single-subject and longitudinal studies.
Discussion
The preliminary results (using 7 subjects) in our on-going pilot study suggest the possibility of atlasing brain regions based on a comprehensive characterization of tissue microstructure described with 3D probability distributions of microscopic water net displacements. Results will be improved by accounting for variation in age and sex in the subject population and scanner specific parameters, by incorporating data obtained using different experimental designs, and by including higher-order terms in the MAP MRI analysis.
Cataloguing and atlasing values of MAP MRI data in normative healthy populations can provide a standard reference for protocol development and data quality assurance in longitudinal and/or multi-center studies, and for clinical studies seeking to detect and characterize subtle microstructural changes, such as those occurring in mild traumatic brain injury (mTBI), neuroinflammation, or metastatic cancer.
Acknowledgements
This work was supported by the Center for Neurodegeneration and Regenerative Medicine (CNRM), under the auspices of the Department of Defense (DoD) and the Henry Jackson Foundation (HJF) grant number #308049-8.01-60855, and by the Intramural Research Program (IRP) of the National Institute of Biomedical Imaging and Bioengineering (NIBIB) and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) within the National Institutes of Health (NIH).References
1 Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys J 66, 259-267 (1994).
2 Mori, S., Oishi, K. & Faria, A. V. White matter atlases based on diffusion tensor imaging. Current opinion in neurology 22, 362-369, doi:10.1097/WCO.0b013e32832d954b (2009).
3 Özarslan, E. et al. Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure. Neuroimage 78, 16-32, doi:http://dx.doi.org/10.1016/j.neuroimage.2013.04.016 (2013).
4 Avram, A. V. et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. Neuroimage 127, 422-434, doi:http://dx.doi.org/10.1016/j.neuroimage.2015.11.027 (2016).
5 Pierpaoli, C. et al. TORTOISE: an integrated software package for processing of diffusion MRI data. Book TORTOISE: an integrated software package for processing of diffusion MRI data (Editor ed.^ eds.) 18, 1597 (2010).
6 Irfanoglu, M. O. et al. DR-TAMAS: Diffeomorphic Registration for Tensor Accurate Alignment of Anatomical Structures. Neuroimage 132, 439-454, doi:https://doi.org/10.1016/j.neuroimage.2016.02.066 (2016).
7 Avram, A. V., Barnett, A. & Basser, P. in Proc Intl Soc Magn Reson Med. 2587.
8 Avram, A. V. et al. in The 23rd Annual Meeting of the International Society for Magnetic Resonance in Medicine 2605.
Figures
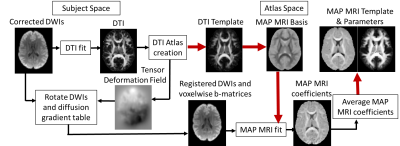
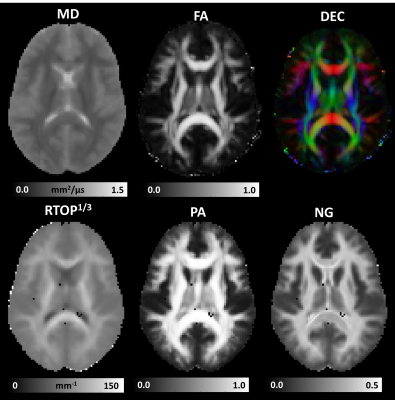
Figure 2: Microstructural MAP MRI parameters computed from the template of 3D diffusion propagators measured in a healthy population: DTI-parameters such as the mean diffusivity (MD), fractional anisotropy (FA), and direction encoded color (DEC) map; along with MAP MRI microstructural parameters such as the Return-to-origin probability (RTOP), Propagator Anisotropy (PA), and Non-Gaussianity (NG).

Figure 3: Visualization of orientation distribution functions (ODFs) derived from the template image of 3D diffusion propagators in a healthy population.