1568
Mitigating the effects of imperfect fixel correspondence in Fixel-Based Analysis1The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia, 2Florey Department of Neuroscience and Mental Health, The University of Melbourne, Melbourne, Australia
Synopsis
A requisite step in performing a Fixel-Based Analysis (FBA) is the determination of "fixel correspondence", which defines how discrete fibre elements (fixels) for a particular subject map to the fixels defined in each voxel in template space. The method used thus far for this purpose - simply selecting the subject fixel that best aligns with the template fixel - fails to take into consideration the possibility for substantial variations in fixel segmentation across subjects. We propose a more sophisticated algorithm for determining fixel correspondence, which better accounts for differences in fixel segmentation, and demonstrate how this reduces the variance observed in fixel data across healthy controls.
Introduction
The Fixel-Based Analysis (FBA) framework allows for the data-driven identification of effects of interest in white matter quantitative measures[1], where statistical inference is both sensitive and specific to effects in individual fibre bundles within voxels ("fixels") even in the presence of crossing fibres. One aspect of this framework that does not have an analogue in conventional Voxel-Based Analysis (VBA) is the necessity to obtain not only spatial alignment of each subject to the template image, but also fixel correspondence between individual subject data and the fixel template. While this process may seem trivial intuitively, imperfections in this correspondence due to differences in fixel segmentation or fibre geometry may contribute significant variance to the data. We propose a method for estimating and accounting for these differences, reducing the impact of this effect on the outcomes of fixel-based analyses.Methods
In the existing publicly-available implementation of FBA[2], for each template fixel, data are extracted from the subject fixel most collinear with the template fixel (as long as the angle between them is no greater than 45 degrees by default).
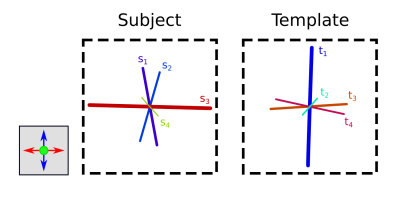
Figure 1 shows an example voxel where the fixel representations vary considerably between subject data and the fixel template. Using the aforementioned approach, the subject quantitative data would be projected to the template as follows (using nomenclature of “target: source”):
$$$t_1:s_2$$$
$$$t_2:$$$
$$$t_3:s_3$$$
$$$t_4:s_3$$$
This demonstrates two issues in particular. Firstly, only information from subject fixel s2 is mapped to template fixel t1, and fixel s1 is omitted; secondly, both template fixels t3 and t4 draw their information from subject fixel s3. For measures of fibre density in particular, these may result in quantitative data for this subject varying substantially from that of other subjects. Note that the angle between t2 and s4 is greater than 45 degrees.
A more appropriate mapping in this case would be:
$$$t_1:s_1,s_2$$$
$$$t_2:$$$
$$$t_3:s_3(shared)$$$
$$$t_4:s_3(shared)$$$
That is: For template fixel t1, information from both fixels s1 and s2 contribute to the measure for this subject; for template fixels t3 and t4, data from subject fixel s3 must be shared between those template fixels.
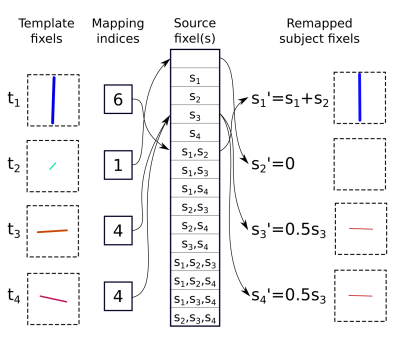
In the proposed method, all possible configurations for the mapping of subject to template fixels are constructed. Here we denote this mapping as M, with elements Mj for j in T (number of template fixels in voxel) listing those subject fixels si for i in S (number of subject fixels in voxel) from which data should be mapped in order to match template fixel tj.
The optimal mapping M is selected based on minimization of the following cost function:
$$f_M=\sum_{j=1...T}(FD_{t_j}-FD_{s'_j})^2\cdot tan(cos^{-1}|⟨\widehat{t_j},\widehat{s'_j}⟩|)+\sum_{i:C(i)=0}FD_{s_i}^2$$
$$$FD_{t_j}$$$ and $$$FD_{s'_j}$$$ are the fibre densities of template fixel tj and remapped subject fixel s'j respectively; $$$\widehat{t_j}$$$ and $$$\widehat{s'_{j}}$$$ are the unit directions of fixels tj and s'j respectively; $$$C(i)=∑_j[s_i \in M_j]$$$ is the frequency with which subject fixel si appears in M; $$$⟨\widehat{t_j},\widehat{s'_{j}}⟩$$$ is the inner product between unit directions $$$\widehat{t_j}$$$ and $$$\widehat{s'_{j}}$$$. Each remapped subject fixel s'j is defined based on the (weighted) combination of those subject fixels being mapped to it according to Mj:
$$FD_{s'_j}=\sum_{s_i \in M_j}\frac{FD_{s_i}}{C(i)}$$
$$\widehat{s'_j}=\widehat{(\sum_{s_i \in M_j}\frac{FD_{s_i}}{C(i)} \cdot \widehat{s_i})}$$
fM is minimal when each remapped subject fixel s'j is both collinear with, and contains the same total fibre density as, corresponding template fixel tj, and no subject fixels si are omitted from the mapping. This process, demonstrated for the optimal mapping for the data in Figure 1, is shown in Figure 2.
Results
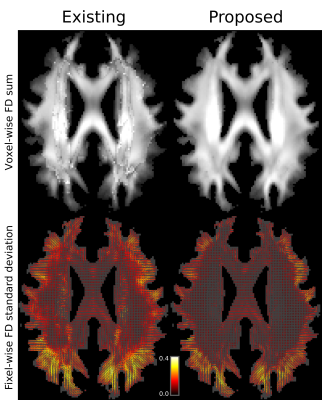
Effects of the proposed fixel matching algorithm on healthy control data mapped to a fixel template are demonstrated in Figure 3.Discussion
By constraining the contribution from each subject to the template based on preservation of fibre volume, the total fibre density within each voxel in the template image no longer contains erroneous local minima or maxima due to imperfect fixel correspondence (Figure 3; top row). In addition, by accounting for more complex fixel mappings to the template, the variance in fibre density between healthy controls is reduced, particularly in deep WM crossing-fibre regions (Figure 3; bottom row).
The proposed approach also enables a number of other potential benefits for FBA; for instance: Omitting individual subject data from particular fixels, or removing fixels from the statistical analysis mask where fixel correspondence is ill-defined; including a measure of fixel correspondence complexity within the General Linear Model (GLM).
Conclusion
The reduction in intrinsic data variance achieved by accounting for more complex fixel correspondence between subject and template space should make future FBA studies more sensitive to pathologies with small effect size, and/or located in regions with complex fibre geometry.Acknowledgements
We are grateful to the National Health and Medical Research Council (NHMRC) of Australia, and the Victorian Government's Operational Infrastructure Support Program for their support.References
- Raffelt, D. A.; Tournier, J.-D.; Smith, R. E.; Vaughan, D. N.; Jackson, G.; Ridgway, G. R. & Connelly, A. Investigating white matter fibre density and morphology using fixel-based analysis. NeuroImage, 2016, 144, 58-73
- www.mrtrix.org
Figures