1567
Clustering of tractography datasets based on streamline point distribution1Faculty of Engineering, University of Concepción, Concepción, Chile, 2Neurospin, I2BM, CEA, Gif-sur-Yvette, France
Synopsis
We propose a fiber clustering algorithm composed by several steps, with the objective of representing the whole dataset by a small set of cluster centroids. First, a clustering is performed separately for a subset of points within the streamlines. The obtained point clusters are then used to regroup the fibers having common point clusters. Next, fiber clusters are filtered out by size and finally regroup using a quick merge based on a maximum Euclidean distance. A reduced set of regular and thin clusters is finally obtained. In contrast to previous works, the proposed method is only based on streamline structure.
Introduction
A big number of methods have been proposed for streamline clustering, along with anatomical information, for the extraction of known fiber bundles [1-4].
More "exploratory" approaches do not try to segment known bundles, but look for a subset of clusters that provide a good description of white matter (WM) structure [5-7]. This representation allows a dimension reduction of the data, to be used as input by other WM analyses. These works are oriented to process large and complex tractography datasets. In [6], several processing steps are applied to subsequently subdivide the fibers into groups, based on different criteria, like brain masks, voxel connectivity, fiber length and pointwise fiber distance. This algorithm leads to regular and thin clusters that represent the structure of the whole (WM) fiber dataset. However a big number of parameters and extra information are used. QuickBundles [7] performs a very fast streamline clustering, basing its speed on a direct assignment of a fiber to a cluster, without further reassignment. The clustering results of this method depend on the initial permutation of input fibers.
We propose a new method for the clustering of large tractography datasets based on fiber point distribution. The main goal is to develop a simple but efficient clustering to regroup fibers into small and regular clusters, representing the whole brain WM structure. A special interest is its use for the study of short association bundles [8], where fibers within a cluster need to be very similar.
Method
We define a clustering process for tractography datasets to discover all disjoint clusters containing a significant number of similar streamlines. We assume a distance metric $$$d(a,b)$$$ to measure the similarity between streamlines $$$a$$$ and $$$b$$$, where streamlines can be stored in direct or reverse (flipped) order.
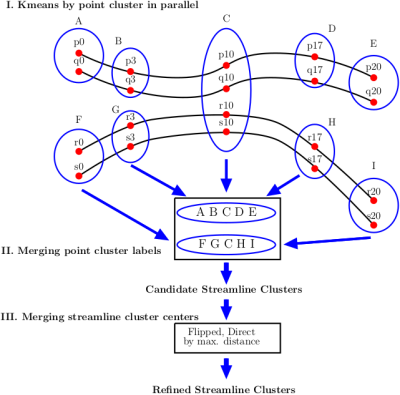
The clustering process consists of three phases (Fig.1):
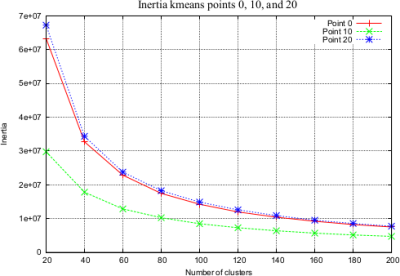
I. Kmeans by point cluster in parallel. We apply Minibatch kmeans [9] over a subset of points on all streamlines. This allows us to group streamlines based on the cluster membership of their points. We apply kmeans in parallel for each point. To estimate the number of clusters in kmeans we use the elbow method [10] (Fig.2).
II. Merging point cluster labels. Since the membership of clusters in kmeans is given by the labels of each point cluster, we represent each streamline by the cluster labels of its points. We build a $$$dictionary$$$ where the $$$key$$$ is the cluster labels that represent each streamline, and the $$$value$$$ is the group of streamlines that share the same key in the dictionary. Fig. 1 shows an example using four streamlines, where after applying parallel Minibatched kmeans over five points in parallel, two Candidate Streamline Clusters are formed, by merging the membership kmeans point clusters. At the end of this phase, we discard groups containing one streamline.
III. Merging streamline cluster centers. This phase performs the merge of streamlines cluster centers by taking their middle point, creating as many groups as the number of clusters defined for the middle point in step I. Each group is formed by all streamline cluster centers that share the middle point cluster. Then, we compute the maximum distance for all streamlines in direct $$$d_{E}$$$ and flipped $$$d_{Eflip}$$$ order in each group, in order to determine de maximum Euclidean Distance between corresponding points $$$d_{ME}$$$ [2]:
$$d_{E}(a,b) = \parallel a_i-b_i\parallel = (\sum_{i=1}^K(a_i-b_i)^2)^{1/2}$$
$$d_{Eflip}(a,b) = d_{E}(a, b^F) = d_{E}(a^F, b)$$
$$d_{ME} = min(max(d_{E}(a, b)), max(d_{Eflip}(a,b)))$$
Finally, we merge all cluster centers with distance $$$d_{ME}(a,b) < d_{max}$$$.
Results
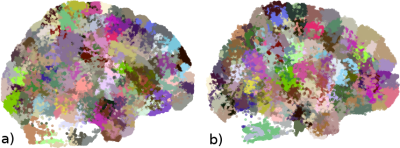
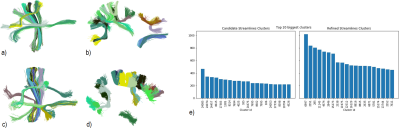
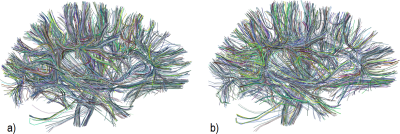
We use a fiber dataset of the left hemisphere of a subject from ARCHI database [11], resampled with 21 equidistant points (258,382 fibers). Next, MiniBatch kmeans was applied to points: 1, 4, 11, 17 and 21, using 150 clusters for each point (step I) (Fig.2). Then, the fibers were grouped using point cluster labels (step II), leading to 41,764 streamline clusters. Clusters with only one fiber were discarded, obtaining 23,660 streamline clusters. Fig.5a shows the centroids of the obtained clusters. Finally, in step III, cluster centroids were merged using distance $$$d_{ME}$$$ and $$$d_{max}=10mm$$$, obtaining 16,497 clusters (Fig.5b). Fig. 4 shows some subsets of clusters obtained for steps II and III. The total execution time was 120s.Discussion and conclusion
We propose a new method for the clustering of WM fiber tractography datasets. Results show an important reduction of the set representation, keeping stringent clusters. The choice of the distance in the final step is important, in particular for the analysis of short association bundles, were a good differentiation of bundles is needed. Future work will evaluate an improvement of this distance.Acknowledgements
This work was supported by CONICYT Chile grants FONDECYT #1161427 and CONICYT-PIA-Anillo ACT1416.References
[1] L. O’Donnell, M. Kubicki, M. Shenton, M. Dreusicke, W. Grimson, and C. Westin, “A method for clustering white matter fiber tracts,” AJNR, American Journal of Neuroradiology, vol. 27, pp. 1032–1036, 2006.
[2] P. Guevara, D. Duclap, C. Poupon, L. Marrakchi-Kacem, P. Fillard, D. Le Bihan, M. Leboyer, J. Houenou,, “Automatic fiber bundle segmentation in massive tractography datasets using a multi-subject bundle atlas,” Neuroimage, vol. 61, no. 4, pp. 1083–1099, 2012.
[3] C. Ros, D Güllmar, M. Stenzel, H.-J. Mentzel, and J. Rainer, “Atlas-guided cluster analysis of large tractography datasets.,” PloS one, vol. 8, pp. e83847, 2013.
[4] Y. Jin, Y. Shi, L. Zhan, B. Gutman, G. Zubicaray, K. McMahon, M. Wright, A. Toga and P. Thompson, “Automatic clustering of white matter fibers in brain diffusion MRI with an application to genetics,” Neuroimage, vol. 100, pp. 75–90, 2014.
[5] E. Visser, E. Nijhuis, J. Buitelaar, and M. Zwiers, “Partition-based mass clustering of tractography streamlines.,”NeuroImage, vol. 54, pp. 303–312, 2011.
[6] P. Guevara, C. Poupon, D. Rivière, Y. Cointepas, M. Descoteaux, B. Thirion, and J.-F. Mangin, “Robust clustering of massive tractography datasets,” Neuroimage, vol. 54, no. 3, pp. 1975–1993, 2011.
[7] E. Garyfallidis, M. Brett, M. Morgado, G. B. Williams, and I. Nimmo-Smith, “Quickbundles, a method for tractography simplification.,” Frontiers in neuroscience, vol. 6, pp. 175, 2012.
[8] M. Guevara, C. Román, J. Houenou, D. Duclap, C. Poupon, J.-F. Mangin, and P. Guevara, “Reproducibility of superficial white matter tracts using diffusion-weighted imaging tractography,” NeuroImage, vol. 147, pp. 703–725, 2017.
[9] D. Sculley, “Web-scale k-means clustering,” in Proceedings of the 19th international conference on World wide web. ACM, 2010, pp. 1177–1178.
[10] C. M. Bishop, "Pattern recognition and machine learning", springer, 2006.[11] B. Schmitt, A. Lebois, D. Duclap, P. Guevara, F. Poupon, D. Rivière, Y. Cointepas, D. LeBihan, J-F. Mangin, and C. Poupon, “Connect/archi: an open database to infer atlases of the human brain connectivity,” in ESMRMB, 2012.
Figures