Synopsis

Hiqh-quality diffusion tractography depends on the accurate estimation of orientation distribution functions (ODFs). Existing estimation methods often use modeling assumptions that are violated by real data, lack theoretical characterization, and/or are only applicable to a narrow class of q-space sampling patterns. As a result, existing approaches may be suboptimal. This work proposes a novel ODF estimation approach that learns a linear ODF estimator from training data. The approach can be applied to arbitrary q-space sampling schemes, has strong theoretical justification, and it can be shown that the trained estimators will generalize to new settings they weren’t trained for.

Introduction

We propose a new method for estimating orientation distribution functions (ODFs) for arbitrary q-space sampling schemes. Existing approaches can broadly be classified as model-based and model-free. Model-based approaches^1-3 are widely used, but rely on modelling assumptions that are commonly violated in the brain⁴. In contrast, model-free approaches^5-8 make fewer assumptions, but it is unclear if existing methods are optimal. Additionally, many of the existing methods^1,2,3,5,6 are not applicable to arbitrary q-space sampling schemes, and instead assume a specific scheme.

This work introduces a new approach, called ERFO (ERF Optimized ODF estimation), that learns an optimal linear ODF estimator from training data and can accommodate arbitrary q-space sampling. Our approach is guided and justified by a recent theoretical framework for linear diffusion estimation⁹.

Methods

The ERFO estimator is designed based on $$$P$$$ training samples, where each sample comprises: (1) ideal noiseless diffusion MRI data $$$E_p\left(\mathbf{q}_m\right)$$$ sampled at $$$M$$$ q-space locations $$$\mathbf{q}_m$$$ and (2) the corresponding ideal noiseless ODF $$$O_p\left(\mathbf{u}\right)$$$, where $$$\mathbf{u}$$$ is the orientation vector. ERFO also assumes that the noise variance $$$\sigma^2$$$ is known. ERFO is designed to estimate ODFs linearly according to: $$\hat{O}(\mathbf{u}) = \sum_{m=1}^M a_m(\mathbf{u}) E\left(\mathbf{q}_m\right),$$ where the ERFO coefficients $$$a_m(\mathbf{u})$$$ are chosen to optimize the minimum mean-squared error loss function (with respect to the training data): $$P\sigma^2 \sum_{m=1}^M |a_m(\mathbf{u})|^2 + \sum_{p=1}^P \left| O_p(\mathbf{u}) - \sum_{m=1}^M a_m(\mathbf{u}) E_p(\mathbf{q}_m) \right|^2.$$ The first term corresponds to estimator noise variance, while the second term corresponds to estimator bias.

The theoretical characteristics of ERFO can be evaluated using EAP response functions (ERFs)⁹, which provide an analytical relationship between a linearly-estimated ODF and the original Ensemble Average Propagator (EAP) through a function known as the ERF. In particular, the term in the ERFO loss function that describes estimator bias can be rewritten in terms of EAPs/ERFs⁹. When expressed in this form, it becomes apparent that the bias term encourages minimal error between the optimized ERF and an ideal ERF, while the training samples define a weighting function on this error. This interpretation is useful because we know that whichever training data we use is unlikely to perfectly match the real tissue characteristics, while the ERF provides a model-free characterization that allows us to nevertheless predict the behavior of the resulting estimator and ensure that it will generalize to contexts it hasn’t been trained for. Even with imperfect training data, the ERFO estimator is still expected to have desirable theoretical characteristics and generalization capabilities as long as the EAP weighting from the training data is reasonably consistent with the true EAP characteristics.

Results

ERFO estimators were designed assuming SNR=35, and multiple b-values (single shell: 3000 s/mm² and 3-shell: 1000, 2000, 3000 s/mm²). We used the DTI model with different orientations and eigenvalues to generate training data.

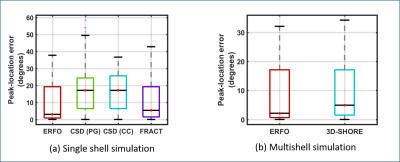
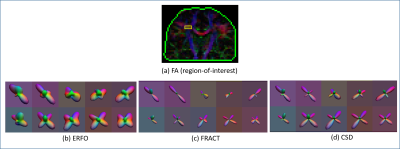
ERFO was tested with simulated and real data. Simulations involved a mixture of two identical infinite cylinders (that do not match the DTI model) crossing at different angles. For single shell data, we compared ERFO with FRACT⁶ and constrained spherical deconvolution (CSD)². For CSD, the single fiber response function was estimated from white matter: (1) near the left postcentral gyrus (PG) and (2) in the corpus callosum (CC). For multishell data, we compared ERFO against 3D-SHORE⁷. In simulations, we quantitatively evaluated angular orientation errors with respect to the ground truth. For in vivo single-shell 64-sample brain data⁸, results were evaluated qualitatively.

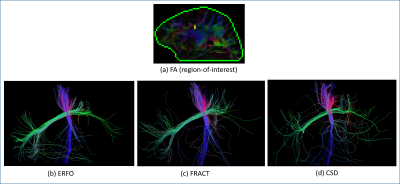
Fig. 1 shows ERFs. In the single shell case, the ERF for ERFO has smaller sidelobes than for FRACT. In the multishell case, the ERF for ERFO has a smaller mainlobe width than for 3D-SHORE. Both of these observations suggest ERFO will have lower estimation error. Fig. 2 shows quantitative results. In the single shell case, ERFO has lower errors than CSD and FRACT. In the multishell case, ERFO has lower errors than 3D-SHORE. Fig. 3 shows estimated ODFs for a section of white matter from in the vivo data. The results show that ERFO and CSD are successful at estimating the orientation corresponding to the superior longitudinal fasciculus, while FRACT has difficulties resolving this orientation. Comparing ERFO and CSD, this orientation is represented more prominently in the ERFO reconstructions. Tractography results from a seed placed in this same region of interest are shown in Fig. 4. While we don’t know ground truth, the ERFO results seem more consistent with expected anatomy.

Conclusions

Acknowledgements

This work was supported in part by research grants NSF CCF-1350563,NIH R21 EB022951, NIH R01 NS074980, and NIH R01 NS089212.

Some of the computation for the work described in this paper was supported by the University of Southern California’s Center for High-Performance Computing (hpc.usc.edu).

Data and simulation acquisition protocol [in part] was provided by the Advanced Biomedical MRI Lab, National Taiwan University Hospital.

Simulation acquisition protocol [in part] was provided by the Human Connectome Project, WUMinn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.

References

[1] P. J. Basser and D. K. Jones, “Diffusion tensor MRI: theory, experimental design and data analysis - a technical review,” NMR Biomed., vol. 15, pp. 456–467, 2002.

[2] J.-D. Tournier, F. Calamante, and A. Connelly, “Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution,” NeuroImage, vol. 35, pp. 1459–1472, 2007.

[3] S. N. Sotiropoulos, S. Jbabdi, J. Xu, J.L. Andersson, S. Moeller, E.J. Auerbach, M.F. Glasser, M. Hernandez, G. Sapiro, M. Jenkinson, D.A. Feinberg, E. Yacoub, C. Lenglet, D.C. Van Essen, K. Ugurbil K, T.E. Behrens, WU-Minn HCP Consortium, “Advances in diffusion MRI acquisition and processing in the Human Connectome Project,” NeuroImage, vol. 80, pp. 125-143, 2013.

[4] S. Jbabdi, S. N. Sotiropoulos, A. M. Savio, M. Graña and T. E. J. Behrens, ”Model-based analysis of multishell diffusion MR data for tractography: How to get over fitting problems,” Magn Reson Med, vol. 68, pp. 1846–1855, 2012.

[5] D. S. Tuch, “Q-ball imaging,” Magn. Reson. Med., vol. 52, pp. 1358–1372, 2004.

[6] J. P. Haldar and R. M. Leahy, “Linear transforms for Fourier data on the sphere: Application to high angular resolution diffusion MRI of the brain,” NeuroImage, vol. 71, pp. 233–247, 2013.

[7] S. L. Merlet and R. Deriche, “Continuous diffusion signal, EAP and ODF estimation via compressive sensing in diffusion MRI,” Med. Image Anal., vol. 17, pp. 556–572, 2013.

[8] F.-C. Yeh, V. J. Wedeen, and W.-Y. I. Tseng, “Generalized q-sampling imaging,” IEEE Trans. Med. Imag., vol. 29, pp. 1626–1635, 2010.

[9] D. Varadarajan and J. P. Haldar, “A theoretical signal processing framework for linear diffusion MRI: Implications for parameter estimation and experiment design,” NeuroImage, vol. 161, pp. 206-218, 2017.