1524

Convolution-Difference Method for Feature Segmentation of Low-Resolution Images
Andrew A Maudsley1

1Radiology, University of Miami, Miami, FL, United States

Synopsis

Automated lesion segmentation of clinical imaging studies is of potential value for treatment monitoring and radiation treatment planning. With low spatial resolution imaging systems, such as MR Spectroscopic Imaging, segmentation based on image intensity variations must take into consideration the broad spatial response function. In addition, the relative lesion-to-background intensity variation and the object size must be considered. In this report a new automated image segmentation method is presented that accounts for these factors, which is based on a subtraction of a smoothed version of the MRSI maps from the original data.

INTRODUCTION

Image segmentation based on intensity variations in low spatial resolution imaging modalities, such as MR Spectroscopic Imaging, must consider the spatial response function (SRF) of the imaging system. In addition, the amplitude threshold that provides an accurate volume determination also depends on the relative signal amplitudes in the region to be segmented and the background1,2. In this study, a novel segmentation method is proposed with the aim of addressing these limitations and the performance evaluated using computer simulations and volumetric MRSI data of brain tumors.

METHODS

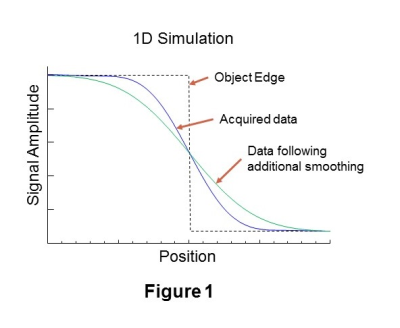
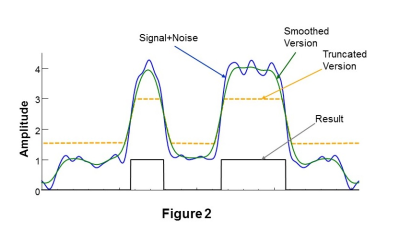
In Figure 1 is shown a simulated one-dimensional cross-sectional profile at the edge of a high signal contrast region (black line). Also shown is the signal, D, that corresponds to the limited k-space sampling of a MRSI dataset with spatial smoothing applied (blue line) and a version of the same signal, D', (green) following additional spatial smoothing. The location of the edge coincides with the position where D=D', and the increased signal region corresponds to where D>D'. This finding must be modified in the presence of noise and Gibbs ringing, as illustrated in Figure 2, which can cause false positives in background regions and false negatives in the high-signal region. It is therefore necessary to modify D' to avoid these ambiguous signal regions, which is done by applying minimum and maximum thresholds, as illustrated by the signal shown in Figure 2 in orange.

The proposed Convolution-Difference segmentation method is therefore as follows:

  1. Create a smoothed version of the data, D'.
  2. Find the data value, DC, where D=D'. This is done by taking the derivative of D' and finding the corresponding data value at the location of the maximum of the derivative.
  3. Truncate D' at a location slightly above DC. A threshold value of DC + 0.25*(D'Max-DC) has been used, where D'Max is the maximum value of D'.
  4. Based on an initial estimate of the high-signal region, determine the mean, M, and standard deviation, SD, of the background signal. Define a lower intensity threshold as M+4*SD and apply this to D'.
  5. Apply the logical operation: Result = D GT D'.

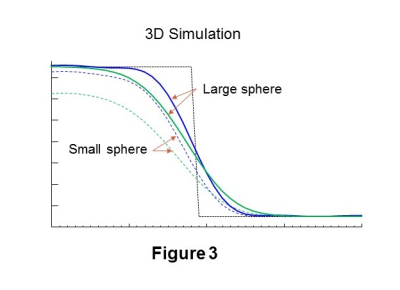
When applied to 3D MRSI the amplitude of D' must be slightly increased to correct for the additive influence of the SRF in multiple dimensions, which is illustrated in Figure 3 using a 3D simulation of two spheres of differing size. In comparison with Figure 1, it can be seen that the location where D=D' no longer corresponds to the edge of the simulated object and that the error is dependent on the object size. The error is also affected by the signal-to-background ratio (SBR). To address this, a scaling factor was determined using a calibration for varying object size and SBR. Since the value of the scaling factor is also dependent on the object size this factor was applied in an iterative manner, using a scaling factor determined from a previous estimate of the object volume and SBR. Typically three iterations were required.

Performance of the proposed segmentation method was evaluated using computer simulation and volumetric MRSI data of brain tumors obtained at TE=70ms.3


RESULTS

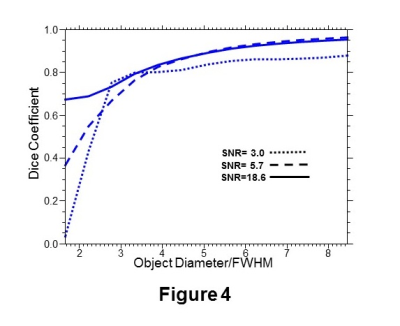
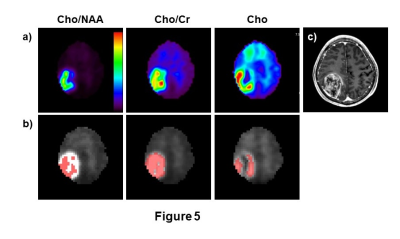
In Figure 4 are shown plots of the Dice coefficient for segmentation of a 3D simulation object defined as a sphere with an intensity gradient, running from 0.5 to 1.0, in one spatial dimension, for three SNR values. Data was simulated for non-isotropic spatial resolution, with 50x50x18 k-space points and nominal voxel size of 5.6x5.6x10 mm3, as is used for a volumetric echo-planar SI acquisition4. In Figure 5 are shown results for a brain tumor segmentation based on the a) Cho/NAA, b) Cho/Cr, and c) Cho signals. Differences in segmentation that reflect different image contrast and heterogeneity in these metabolite maps are apparent.

DISCUSSION

The proposed segmentation method represents a novel approach to image segmentation for imaging modalities that have relatively poor spatial resolution. Simulation studies indicate good performance, although degrading for small objects where the object diameter is on the order of the width of the SRF. Preliminary evaluations for volumetric MRSI indicate differing results for segmentation of brain tumors based on maps of Cho/NAA, Cho/Cr, and Cho and further studies are required to determine which if these is the most robust as well as to optimize performance and determine the most suitable MRSI parameters for lesion segmentation.

Acknowledgements

This work was supported by NIH grants R01EB016064 and R01CA172210. We thank Dr. R.K. Gupta for acquisition of the data shown in Figure 5.

References

1. Jentzen, W., Freudenberg, L., Eising, E.G. et al. Segmentation of PET volumes by iterative image thresholding. J Nucl Med 2007;48(1):108-114.

2. Zaidi, H., and El Naqa, I. PET-guided delineation of radiation therapy treatment volumes: a survey of image segmentation techniques. Eur J Nucl Med Mol Imaging 2010;37(11):2165-2187.

3. Roy, B., Gupta, R.K., Maudsley, A.A. et al. Utility of multiparametric 3T MRI for glioma characterization. Neuroradiology 2013;55(5):603-613.

4. Maudsley, A.A., Domenig, C., Govind, V. et al. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI). Magn Reson Med 2009;61(3):548-559.

Figures

Simulation showing the relationship between the edge of an image feature (black line) and the resultant signal detected with typical MRSI acquisition parameters (blue). Also shown is the result of applying additional smoothing to the data (green). The edge of the object coincides to the point where the blue and green plots have equal value.

Simulation for a 1D example showing the effect of noise and Gibbs ringing on the data (blue) and smoothed version of the data (green). By applying thresholds for minimum and maximum data values the true boundaries of the high-signal regions can be identified where the data is larger than the smoothed version, and the result is shown in black.

1D profiles through the edge of a spherical volume of high signal intensity simulated for a sphere, shown for the original data (blue) and a smoothed version of that data (green). Results are shown for two sizes of the simulated sphere, using the solid and dashed lines. In comparison to the result shown in Figure 1, the edge of the high signal region is no longer coincident with the cross-over point due to the additive influence of the SRF in the orthogonal directions.

Plot of the Dice coefficient that indicates the degree of agreement between a segmentation of a spherical object volume and the actual extent of that object. Data is shown for three value of the SNR, defined as the ratio of the peak signal amplitude to the RMS noise in the object background region. The object diameter is defined as a fraction of the SRF used for the image simulation. The simulation used parameters that correspond to existing MRSI methods, for which the FWHM of the SRF was determined to be 9.8 mm in-plane and 15.4 mm through-plane.

Example segmentations for a volumetric MRSI study of a glioblastoma. In (a) are shown color maps for Cho/NAA, Cho/Cr, and Cho, each windowed at 90% full scale, which demonstrate the heterogeneity within the tumor and the large range in contrast between the different metabolite maps. In (b) are shown the corresponding image segmentations. The post contrast T1 MRI is shown in (c).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1524