1519

Assessment of Approximated Analytical B1+ Correction Method for prostate DCE-MRI with Multiple Noise Levels and in 3.0 T Systems

Xinran Zhong^1,2, Thomas Martin^1,2, Steve Raman¹, Holden H Wu^1,2, Krishna Nayak³, and Kyunghyun Sung^1,2

¹Department of Radiological Sciences, University of California, Los Angeles, Los Angeles, CA, United States, ²Physics and Biology in Medicine IDP, University of California, Los Angeles, Los Angeles, CA, United States, ³Ming Hsieh Department of Electrical Engineering, University of Southern California, Los Angeles, CA, United States

Synopsis

B₁⁺ correction is essential for quantitative prostate DCE-MRI. A simplified approximated analytical B₁⁺ correction method was proposed previously, and we assess this method on a digital reference object (DRO) with various SNR levels and on 110 in-vivo cases from two 3.0 T systems. We find that the approximated analytical B₁⁺ correction method achieves comparable performance to conventional correction method with substantially reduced computation. The approximated analytical correction method is simple and practical for application in the clinic.

INTRODUCTION

Dynamic contrast-enhanced MRI reveals tissue vasculature properties and is useful for the diagnosis and monitoring of prostate cancer¹. Quantitative analysis is mainly comprised of MRI signal modeling to generate the contrast agent concentration vs. time curve and pharmacokinetic (PK) modeling to generate K^trans and v_e maps. Accurate quantification is challenging due to many factors, including B₁⁺ inhomogeneity. B₁⁺ inhomogeneity leads to flip angle variation and is known to introduce significant error into the quantification results². Even when B₁⁺ estimates are available, B₁⁺ correction can be computationally burdensome. Recently we proposed an approximated analytical B₁⁺ correction method³, and have validated it in simulation and with a digital reference object (DRO)⁴. Here, we further evaluate this B₁⁺ correction method on DRO with various SNR levels and on 110 in-vivo cases and compare it with conventional numerical correction method⁵.

METHODS

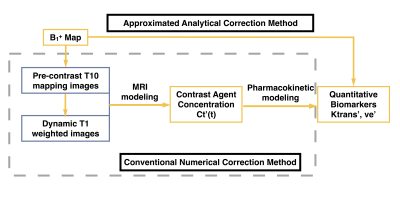
As described previously³, we proposed an approximated analytical B₁⁺ correction method which only takes the B₁⁺ map and uncorrected PK maps as the input. It is easy to implement and can reduce the computation time. The comparison between proposed approximated correction and conventional numerical correction is shown in Fig. 1.

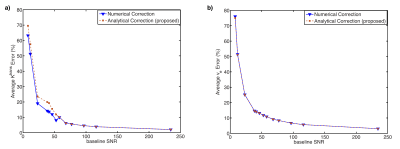
To evaluate our proposed method, we created a prostate-specific digital reference object (DRO) based on the RSNA Quantitative Imaging Biomarkers Alliance (QIBA) project with our clinical protocol⁴. The DRO comprised of a series of realistic ground truth K^trans (ranged from 0.01 to 0.35 min^-1) and v_e (ranged from 0.01 to 0.5). Noise was added to each DRO images using the equation $$$\sqrt{(R+r_1)^2+r_2^2}$$$, which is similar to QIBA DRO v9⁶. R is the original signal, and r₁ and r₂ are noise with mean zero and standard deviation ranging from 5 to 150. The resulting baseline SNR of the DCE signal is from 7.8 to 234.5. With noise added in all DRO images, B₁⁺ corrected PK maps using two correction methods were calculated for each noise level, and both correction methods were evaluated using mean percentage error compared to the ground truth PK parameters.

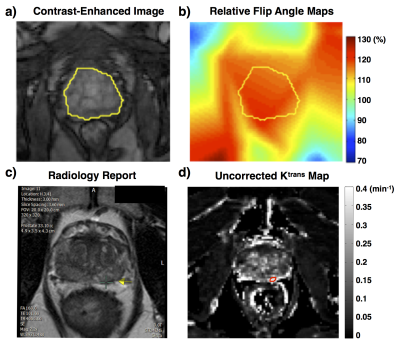
With IRB approval, 110 prostate patients acquired from two 3.0T systems (MAGNETOM Skyra and MAGNETOM Trio, Siemens Medical Systems) were retrospectively selected to evaluate the approximated analytical correction by comparing with the conventional numerical correction. For each case, relative flip angle maps were generated based on RR-VFA method^7,8, and three K^trans and v_e maps were calculated (uncorrected, approximated analytically corrected, and numerically corrected). Due to data availability, volumetric regions of interest (ROI) of the prostate region were defined for 82 cases, and the lesions on another 28 cases from the same RF system were contoured based on radiology report, as shown in Fig. 2. The approximated analytical correction method was evaluated using percentage error compared to the numerical corrected PK maps. All post-processing was implemented using an in-house script written in Matlab (Mathworks, Inc., Natick, MA, USA). Estimation parameters (K^trans or v_e) larger than 1 were excluded as outliers⁹.

RESULTS and DISCUSSION

In the DRO experiment, the correction error with different levels of baseline SNR is shown in Fig. 3. Both correction errors decrease with increased baseline SNR level, and the difference between two correction methods is minimal compared to noise-induced correction error. Also, the numerical correction error has a minimum of 2.1%±4.3% with the maximum SNR of 234.5 in the simulation, which gives the correction uncertainty from noise.

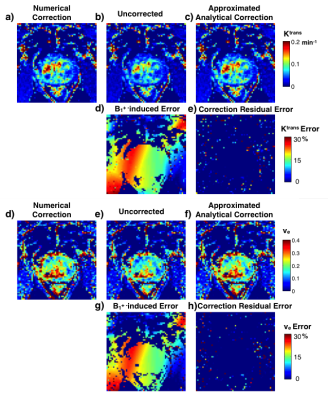
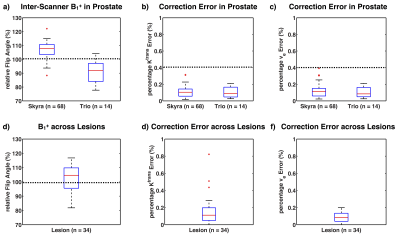
Fig. 4 shows an example in-vivo case with PK maps and error maps. The error induced by the approximation is negligible compared to error induced by B₁⁺ variation. Among the 82 cases, the percentage error of the approximated analytical correction is 0.11±0.27% for K^trans, and 0.11±0.38% for v_e. Fig. 5 shows the B₁⁺ distribution and the approximated analytical correction error for both prostate ROI and lesion ROI. The B₁⁺ patterns between two scanners (Fig. 5a) are significantly different (p < 0.05), indicating the necessity of B₁⁺ correction for comparison between scanners. Similarly, within lesion ROIs, the average B₁⁺ varies from 81.8% to 116.8%, showing the necessity for B₁⁺ correction for lesion characterization. For all the evaluations, the K^trans and v_e errors are less than 0.4%, which is much smaller than the noise-induced uncertainty. Additionally, our proposed correction method computationally took 0.01s for a typical 3D volume cases, while the conventional correction methods took more than 3 hours with our implementation. Our proposed correction method can be a good alternative under some condition regarding computation efficiency.

CONCLUSION

The approximated analytical correction method gives comparable results to conventional numerical correction. This is a practical alternative to conventional B₁⁺ correction for prostate DCE-MRI.

Acknowledgements

This work was supported in part by the Integrated Diagnostics Program, Departments of Radiological Sciences at UCLA.

References

1. Franiel T, Hamm B, Hricak H. Dynamic contrast-enhanced magnetic resonance imaging and pharmacokinetic models in prostate cancer. European Radiology. 2011;21:616–626.

2. Di Giovanni P, Azlan CA, Ahearn TS, Semple SI, Gilbert FJ, Redpath TW. The accuracy of pharmacokinetic parameter measurement in DCE-MRI of the breast at 3 T. Physics in Medicine and Biology. 2010;55(1):121–132.

3. Zhong X, Rangwala N, Raman S, Margolis D, Wu H, Sung K. B1+ Inhomogeneity Correction for Estimation of Pharmacokinetic Parameters through an Approximation Approach. Proceedings 24th Scientific Meeting, International Society for Magnetic Resonance in Medicine. 2016:2491.

4. Zhong X, Wu H, Nayak K, Sung K. Evaluation of Approximation Method for B1+ Correction using Digital Reference Object in Prostate DCE-MRI. Proceedings 25th Scientific Meeting, International Society for Magnetic Resonance in Medicine. 2017:622.

5. Bedair R, Graves MJ, Patterson AJ, McLean MA, Manavaki R, Wallace T, Reid S, Mendichovszky I, Griffiths J, Gilbert FJ. Effect of Radiofrequency Transmit Field Correction on Quantitative Dynamic Contrast-enhanced MR Imaging of the Breast at 3.0 T. Radiology. 2015;279(2):150920.

6. QIBA Content | Daniel P. Barboriak Lab. https://sites.duke.edu/dblab/qibacontent/

7. Sung K, Saranathan M, Daniel BL, Hargreaves BA. Simultaneous T 1 and B 1 + Mapping Using Reference Region Variable Flip Angle Imaging. Magnetic Resonance in Medicine. 2013;70(4):954–961.

8. Rangwala NA, Dregely I, Wu HH, Sung K. Optimization and evaluation of reference region variable flip angle (RR-VFA) B1+ and T1 Mapping in the Prostate at 3T. Journal of Magnetic Resonance Imaging. 2017;45(3):751–760.

9. Peng Y, Jiang Y, Yang C, Brown JB, Antic T, Sethi I, Schmid-Tannwald C, Giger ML, Eggener SE, Oto a. Quantitative analysis of multiparametric prostate MR images: differentiation between prostate cancer and normal tissue and correlation with Gleason score--a computer-aided diagnosis development study. Radiology. 2013;267(3):787–796.

Figures

Figure 1. Comparison between the two B₁⁺ correction approaches. Conventional correction method needs to repeat MRI modeling and PK modeling pixel by pixel with original T₁₀ images and dynamic T₁ weighted images, while approximated analytical correction method only requires the uncorrected PK parameters to perform the correction and simplifies the computation.

Figure 2. Comparison of correction residual errors between two correction methods for K^trans maps (a) and v_e maps (b) with various levels of noise added. There are 100 Monte-Carlo simulations for each PK parameter combination. For each SNR level, noise-induced errors for 3000 pixels (5 × 6 × 100) excluding outliers were averaged.

Figure 3. Example of ROI positioning for prostate (a-b) and lesion (d). The volumetric prostate ROI is defined by contrast-enhanced images, and the 2D lesion ROI is defined on uncorrected K^trans maps based on the radiology report (d).

Figure 4. K^trans maps after numerical B₁⁺ correction method (a), before B₁⁺ correction (b) and after approximated analytical correction method (c), B₁⁺ induced error for Ktrans (d), correction residual error of K^trans (e), v_e maps after numerical B₁⁺ correction method (f), before B₁⁺ correction (g) and after approximated analytical correction method (h), B₁⁺ induced error for v_e (i), and correction residual error of v_e (j).

Figure 5: Boxplot of average relative flip angle (%) distribution between two 3.0 T systems (a) and corresponding correction residual error for K^trans (b) and v_e (c) within volumetric prostate ROIs for 82 patients. Boxplot of average relative flip angle (%) distribution across 34 lesions within 2D ROI from 28 in-vivo cases (d) and corresponding correction residual error for K^trans (e) and v_e (f). All correction errors are smaller than 1%.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1519