1497
Bio Heat Transfer Model Based Temporally Constrained Reconstruction for Accelerated MR Temperature Imaging1Department of Biomedical Engineering, Tsinghua University, Beijing, China, 2Department of Engineering Physics, Tsinghua University, Beijing, China, 3Department of Orthopedics, First Affiliated Hospital of PLA General Hospital, Beijing, China, 4Key Laboratory of Particle and Radiation Imaging, Ministry of Education, Medical Physics and Engineering Institute, Tsinghua University, Beijing, China
Synopsis
Thermal therapies require accurate and real-time temperature monitoring to guide the treatment. To achieve higher temporal resolution in MR temperature imaging, we introduced bio heat transfer model to predict temperature maps, which are combined with previous image to act as constraints in the reconstruction of under-sampled data. An inverse optimization is also included to make the BHT model self-adaptive. Through robustness verifying experiment and heating simulation, the ability of the proposed method to provide accurate reconstruction at a high reduction factor is demonstrated in this study.
Introduction
Proton resonance frequency (PRF) shift1 based MR thermometry has been used in thermal therapies to monitor the temperature. High temporal resolution is required to improve the efficiency and safety in clinical applications. Recently, the TCR2 and PITCR3 methods using a temporal constraint were proposed to improve the temporal resolution. In these two methods, images at adjacent time frames are used by data sharing reconstruction, and a reduction factor of 4-6 can be achieved. However, using the subsequent time frame leads to a delay of temperature monitoring, while relying on previous information alone can result in underestimation or overestimation. Such drawback will lead to inaccurate temperature estimation especially when temperature changes dramatically or a high reduction factor is pursued. To solve this problem, a self-adaptive BHT model is introduced to predict the temperature maps, which are combined with the previously reconstructed image to act as constraints.Method
Theory:
The bio heat transfer (BHT) model is based on the Pennes equation4:
$$\rho C \frac{\partial T}{\partial t} = K \Delta ^{2} T + W_b C_b (T_b -T) + Q_r + Q_m $$
where $$$T$$$ is the tissue temperature, $$$\rho$$$ is the tissue density, $$$C$$$ and $$$C_b$$$ are the specific heat of the tissue and blood respectively, $$$K$$$ is the thermal conductivity, $$$W_b$$$ is the perfusion rate, $$$T_b$$$ is blood temperature, $$$Q_r$$$ is the heat source, and $$$Q_m$$$ is the metabolic heat generation.
For each time frame t, the temperature image is estimated by minimizing the following cost function:
$$\min_{\tilde{m}} \left( \Vert WF\tilde{m} -d\Vert _2 ^2 + \lambda \left[ (1-\alpha)\Vert\Delta _t \tilde{m} \Vert _2^2 + \alpha \Vert \tilde{m}-m_{t,BHT}\Vert _2^2 \right] \right)$$
where $$$\tilde{m}$$$ is the image estimate, $$$d$$$ is the under-sampled k-space data, $$$F$$$ is 2D Fourier Transform and $$$W$$$ is a sparsifying function corresponding to the under-sampling pattern, $$$m_{t,BHT}$$$ is the prior information predicted by BHT model. The temporal constraint is:
$$\Delta _t \tilde{m} = m_{t-1} - 2 \tilde{m} + m_{t+1,BHT} $$
where $$$m_{t+1,BHT} $$$ is also given by BHT model.
For each time frame, the newly obtained image is used as reference to optimize the parameters of the BHT model inversely, and the result will be used in the estimation for the next time frame.
Experiments:
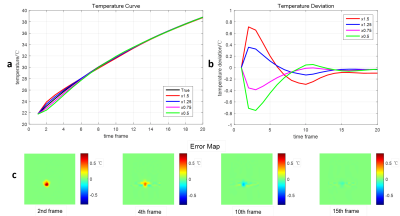
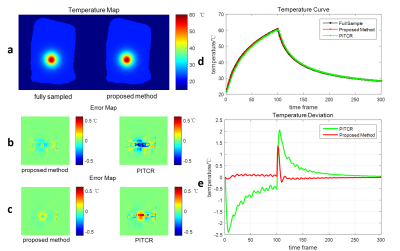
A robustness verifying experiment and a heating simulation were performed to investigate the feasibility and the robustness of the proposed method. In the robustness verifying experiment, the initial power of heat source was set to be 150%, 125%, 75%, and 50% of the proper value respectively, and the subsequent performance of the model was observed. In the simulation, 12.5% sampled data was used (R = 8), and the proposed method was compared with PITCR in the heating as well as cooling process.
Results
The results of the robustness verifying experiment are shown in Fig 1. Regardless of the deviation in parameter in the beginning, the performance of the model will be relatively accurate after several time frames. The results of the heating simulation are shown in Fig 2. A temperature map without aliasing artifacts can be obtained with 12.5% sampled data by using the proposed method. As can be seen in Fig 2(e), the temperature errors of the proposed method are under 0.5℃ in most time frames, while large errors up to 2℃ can be seen using PITCR, especially when the temperature changes fast. During the period shortly after the turning point, the errors of the proposed method exceed 0.5℃, which, however, are still far better than the result of PITCR. Fig 2(b) and Fig 2(c) show the error map during heating and cooling process respectively. It can be seen that the problems of underestimating in heating and overestimating in cooling are mitigated by the proposed method. The root-mean-square errors (RMSEs) are listed in Table 1, where the proposed method results in less RMSEs than PITCR.Discussion & Conclusion
The BHT model is introduced to provide predictive information in the reconstruction of highly under-sampled k-space data. The robustness verifying experiment demonstrates that the BHT model is self-adaptive and the proposed method is robust with model parameter error. The heating simulation validates that the proposed method can reconstruct more accurate temperature images with high reduction factor or fast temperature changes. Better temporal resolution is also provided by avoiding using data at the next time frame. Further ex-vivo and in-vivo studies should be done to evaluate the accuracy of the proposed method.Acknowledgements
This study was supported by National Natural Science Foundation of China: NSFC 6177010624.References
1. Ishihara Y, Calderon A, Watanable H, et al. A precise and fast temperature mapping using water proton chemical shift. Magnetic Resonance in Medicine, 1995, 34: 814-823.
2. Todd N, Adluru G, Payne A, et al. Temporally constrained reconstruction applied to MRI temperature data. Magnetic Resonance in Medicine, 2009, 62:406-419.
3. Prakash J, Todd N, Yalavarthy P K. Prior image based temporally constrained reconstruction algorithm for magnetic resonance guided high intensity focused ultrasound. Medical Physics, 2015, 42:6804-6814.
4. Pennes H H. Pennes HH Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol 1:93-122. Journal of Applied Physiology, 1998, 85:5-34.
Figures