1382
Simulated 1H-1H residual dipolar couplings of collagen-associated water1Research Unit of Medical Imaging, Physics and Technology, University of Oulu, Oulu, Finland, 2Department of Applied Physics, University of Eastern Finland, Kuopio, Finland, 3Medical Research Center, University of Oulu and Oulu University Hospital, Oulu, Finland, 4Department of Diagnostic Radiology, Oulu University Hospital, Oulu, Finland
Synopsis
Residual dipolar couplings have been suggested as the cause of the orientational dependence of relaxation times in anisotropic tissues, such as articular cartilage. We use molecular dynamics simulations to compute the residual dipolar couplings of water protons associated with a model collagen molecule. The results suggest that significant residual dipolar couplings appear without strong binding between the water and the collagen.
Introduction
Precise and quantitative assessment of the status of articular
cartilage with MRI is
very challenging. A multitude of quantitative methods exist, but most
of them are sensitive to cartilage orientation.1 Residual dipolar coupling (RDC) has been shown to create an
orientation-dependent factor to $$$T_2^{-1}$$$ and to modulate
$$$T_{1\rho}^{-1}$$$ in suitable conditions.2,3 The
purpose of this study is to estimate the strength of the RDC of water protons in a collagenous tissue, using classical molecular dynamics (MD) simulations. The
simulation produces an approximate trajectory for each atom in the
system by integrating Newtonian equations of motion.Theory
In this study we concentrate on dipole-dipole couplings between hydrogens due to
their large gyromagnetic ratio and abundancy as compared to any other
nuclei in collagenous tissues. The 1H-1H RDC "constant" (in frequency units) is the ensemble average
$$d = - \frac{\gamma^2 \mu_0 \hbar}{4 \pi^2} \left\langle \frac{1}{2 r^3}(3 \cos^2 \theta - 1) \right\rangle$$
Here, $$$r$$$
is the length of the vector r connecting the
nuclei. $$$\theta$$$ is the angle between r
and
the
main magnetic field.
Modeling
Type II collagen is a significant constituent of articular
cartilage and other cartilaginous tissues.4 Here,
dipolar couplings of water protons are computed from the
MD simulation trajectory
of a fully solvated collagen-like peptide 1QSU.5 Water is simulated using the TIP4P/2005 model, which is known to
reproduce well the reorientational motion of bulk water.6,7
The peptide is surrounded by at least 20 Å of water on all sides,
totaling N=18393
water molecules. The triple-helical peptide and its
first hydration layer are shown in Figure
1. The simulations are run with NAMD8
software at constant temperature, T=300
K, and pressure, P=1 atm for more than 18 ns.Results
RDC, as in Eq.
1, are computed for water protons in
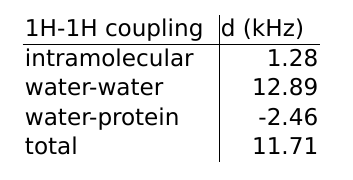
the first hydration layer of the collagen-like peptide (Figure 1). The first hydration layer is defined as the water molecules with any atom less than 3.5 Å from any peptide atom. The results are listed in Table 1. The main magnetic field is assumed to be parallel to
the long axis of the peptide. To take into account different orientations and/or anisotropy of the collagen, one should scale the results with $$$P_2(\cos \beta)$$$, where $$$\beta$$$ is the angle between the peptide and and the main magnetic field. A 20 Å cutoff is used for the intermolecular couplings to mitigate inevitable finite size artefacts. We find that the intermolecular RDCs are much
stronger than the intramolecular couplings. In total, the water-protein RDCs partly cancel out the couplings between
protons in water molecules.
Discussion
The intramolecular RDC are quite well described by our simple model, since only the immediate surroundings of the water molecule affect its rotational dynamics. The intermolecular RDCs simulated with an isolated peptide are not so readily transferable to tissue MRI because e.g. inside fibrils, the distance between adjacent collagen molecules is less than 10 Å. If we dilute our first hydration layer intramolecular coupling with bulk water coupling (zero) to mimic a 10-20 w-% concentration of collagen,9 we get in the range of 165-367 Hz. This agrees well with experimental estimates of RDC in articular cartilage.10
Anisotropic, decelerated motion of bound water has been suggested as the source of RDC in collagenous tissues.11 In our view, this seems unlikely, due to the smallness of the simulated intramolecular RDC as compared to the intermolecular contributions, and in light of short residence and correlation times of water molecules bound to the peptide.12 Furman et al. suggest anisotropically restricted diffusion as the source of RDC,13 but their model ignores the intermolecular dipolar couplings between water and collagen protons. In MR measurements of tissues, intermolecular couplings are affected by diffusional averaging. This could be modeled with simulations of water in a more restricted environment, such as inside a collagen fibril.14 Accumulated dipolar couplings can be significant over large distances,15 however, and pose a challenge to atomistic modeling.
Conclusions
We use molecular dynamics simulations to compute residual dipolar couplings of water protons close to a collagen-like peptide. Our data shows that the simple vicinity of a linear, collagen-like peptide results in an intramolecular RDC, which could be significant for magnetic relaxation in anisotropic tissues, such as articular cartilage. The simulated intermolecular (water-water and the water-macromolecule) couplings bring even stronger contributions, but their relative importance to tissue MRI remains unsolved due to the limitations of our model. Our results raise doubts about some of the common interpretations of the sources of orientation-dependency of relaxation times in collagenous tissues, such as the need for strongly bound water on the collagen surface.Acknowledgements
Jane and Aatos Erkko Foundation as well as the Academy of Finland (grants #285909 and #293970) are gratefully acknowledged for financial support. CSC - IT Center for Science provided the computational resources.References
1. Hänninen, N., Rautiainen, J., Rieppo, L., Saarakkala, S. & Nissi, M. J. Orientation anisotropy of quantitative MRI relaxation parameters in ordered tissue. Scientific Reports 2017; 7: 9606.
2.Baugh, J., Kleinhammes, A., Han, D., Wang, Q. & Wu, Y. Confinement Effect on Dipole-Dipole Interactions in Nanofluids. Science 2001; 294: 1505–1507.
3. Chaumette, H., Grandclaude, D., Brondeau, J., Werbelow, L. & Canet, D. Rotating-frame spin—lattice relaxation measurements (T1rho) with weak spin-locking fields in the presence of homonuclear dipolar coupling. Mol. Phys. 2003; 101: 1919–1926.
4. Fratzl P. Collagen: Structure and Mechanics. Springer Science & Business Media, 2008.
5. PDB ID: 1QSU. Kramer R Z, Venugopal M G, Bella J, et al. Staggered Molecular Packing in Crystals of a Collagen-like Peptide with a Single Charged pair. J. Mol. Biol. 2000; 301(5): 1191–1205.
6. Abascal J L F, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005; 123: 234505.
7. Vega C, Abascal J L F. Simulating water with rigid non-polarizable models: a general perspective. Phys. Chem. Chem. Phys. 2011; 13: 19663–19688.
8. Phillips J C, Braun R, Wang W, et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005; 26: 1781–1802.
9. Fox, A. J. S., Bedi, A. & Rodeo, S. A. The Basic Science of Articular Cartilage. Sports Health 2009; 1: 461–468.
10. Akella, S. V. S., Regatte, R. R., Wheaton, A. J., Borthakur, A. & Reddy, R. Reduction of residual dipolar interaction in cartilage by spin-lock technique. Magn. Reson. Med. 2004; 52: 1103–1109.
11. Fullerton, G. D. & Rahal, A. Collagen structure: The molecular source of the tendon magic angle effect. J. Magn. Reson. Imaging 2007; 25: 345–361.
12. Karjalainen, J., Hanni, M., Nissi, M. J. & Nieminen, M. T. Simulated reorientational correlation times of collagen-associated water. in Proc. Intl. Soc. Magn. Reson. Med. 2017; 25: 1552.
13. Furman, G. B., Goren, S. D., Meerovich, V. M. & Sokolovsky, V. L. Anisotropy of spin–spin and spin–lattice relaxation times in liquids entrapped in nanocavities: Application to MRI study of biological systems. J. Magn. Reson. 2016; 263: 71–78.
14. Streeter, I. & de Leeuw, N. H. Atomistic Modeling of Collagen Proteins in Their Fibrillar Environment. J. Phys. Chem. B 2010;114: 13263–13270.
15. Lee, S., Richter, W., Vathyam, S. & Warren, W. S. Quantum treatment of the effects of dipole–dipole interactions in liquid nuclear magnetic resonance. J. Chem. Phys. 1996; 105: 874–900.