1320
NMRScopeB – an open-source simulator for metabolite quantitation and pulse sequence development1Magnetic Resonance and Cryogenics, Institute of Scientific Instruments of the CAS, Brno, Czech Republic
Synopsis
The architecture and function of the release version of a spectroscopic simulator NMRScopeB is described. It includes the jMRUI-related GUI and an open-source calculation server communicating with the kernel via sockets. While standard metabolite set simulations needed for quantitation by jMRUI or LCModel can be prepared in a few steps, more complex research task can be handled as well. The operation is described by control and data flow charts. After a period of beta-testing, the simulator is released as part of the recent jMRUI package.
Introduction
Quantitation of metabolite concentrations from MR spectroscopic signals is based on their decomposition into basis signals describing individual metabolites. These components have to be prepared by measurement or simulation. If the pulse sequence and NMR properties of metabolite molecules are sufficiently known, simulation is more practical because the need for chemicals, sample preparation and frequency and signal intensity calibration is eliminated. Simulation can also handle any changes in the pulse sequence (timing, RF pulses, flip angles, bandwidths etc.), needed e.g. by RF limitations due to coil selection and loading, optimization for specific metabolites or compatibility with other measurements. Simulation is also useful for the development and testing of customized pulse sequences for MRS or MRI. Although several simulators of coupled spin systems have been described 1, each has some obstacles to their general use (need for serious programming, lack of graphical user interface, lack of generality for in vivo applications, black-box operation, proprietary nature). After extensive testing, we introduce here NMRScopeB as a general tool capable of satisfying most practical spectroscopic needs and providing the physical insight needed for pulse sequence development and education, with continuously expanding functionality.Methods
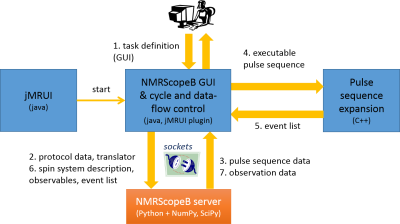
The software is implemented as a plugin of jMRUI (Fig. 1), providing metabolite basis set directly applicable in quantitation by jMRUI’s QUEST 2 or AQSES 3, but also in other quantitation software (e.g. LCModel 4). The module expands jMRUI’s GUI (java) and employs an open-source NMRScopeB server (Python 2.7) executing the pulse-sequence specific operations for the definition of protocol GUI, pulse sequence parameter calculation based on protocol parameters, and quantum-mechanics based simulation. This server communicates via sockets and in principle may be run on a remote server. An auxiliary module (C++) serves the kernel’s need for extensive event list ordering, thanks to which overlapping RF and gradient modulations and arbitrary observations can be easily implemented. In the simplest scenario, the GUI gives the user a possibility to select metabolites for the basis, define the field strength and reference frequency, select a protocol, set its parameters, visually inspect the pulse sequence, run the simulation and save the results. The calculation lets the density operator evolve under the master equation
$$\frac{d}{dt}\hat{\sigma}=-i\left[\hat{H}(t),\hat{\sigma}(t)\right]-\hat{\hat{R}}\left(\hat{\sigma}(t)-\hat{\sigma}_{eq} \right)$$
discretized into a sequence of alternating steps
$$\hat{\sigma}_H(t_k)=\exp(-i\hat{H}(t_k)dt)\hat{\sigma}(t_k)\exp(i\hat{H}(t_k)dt)$$
$$\hat{\sigma}(t_{k+1})=\exp(-\hat{\hat{R}}dt)\hat{\sigma}_H(t_k)+(\hat{\hat{1}}-\exp(-\hat{\hat{R}}dt))\hat{\sigma}_{eq}$$,
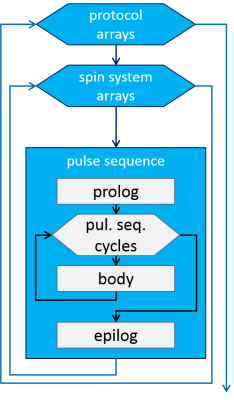
which besides Zeeman and spin-spin interactions (in the Hamiltonian) may involve relaxation (Redfield superoperator R). The resulting signals can be post-processed to include a prior knowledge of lineshapes and filter response. An advanced user may benefit from free construction of molecule definitions and from the support of defining arbitrarily arrayed parameters of the spin systems, the instrument, and the pulse sequence (Fig. 2). Besides the set of general-purpose shaped pulses, arbitrary shapes can be defined in text files and then applied. VERSE-remastering is supported. The excitation can be handled through a set of predefined protocols (incl. onepulse, (MEGA-)PRESS, (MEGA-)STEAM, SPECIAL, (MEGA-)(semi-)LASER), which can be used as patterns for own pulse sequence development. New sequences can be developed on a low-level basis and later equipped with the protocol envelope, or derived from existing protocols. Besides phase cycling, an efficient task-adjustable coherence-transfer-pathway selection mechanism is ensured by Fourier-based implementation of crushers. In case of multidimensional or dynamic simulations, e.g. for teaching purposes, export to Matlab and example visualization scripts are available. The data flows are mainly based on text data files in order to support transparency (Fig. 3). Windows and Linux versions are provided.
Results
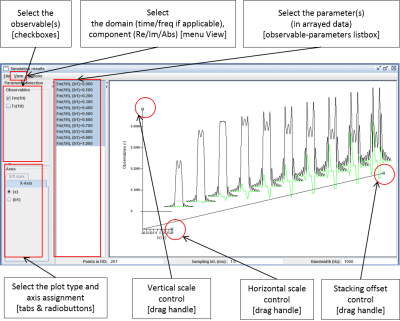
The simulator has been tested on selected tasks against NMRScope 5 and GAMMA 6, experimentally by experienced spectroscopists at several sites and applied in quantification by jMRUI and LCModel at 3-9.4T fields with STEAM, PRESS, SPECIAL, and verified for GABA-edited MEGA-PRESS. It has also been used successfully for the implementation of T2-selective excitation for UTE MRI at a clinical scanner. Beta-user feedback was reflected in optimizing the built-in interface for serialized simulations (Fig. 4). In artifact-free spectra, excellent match between simulated and measured spectra was found.Conclusions
NMRScopeB can be considered a well-tested tool for routine as well as sophisticated simulations predominantly for in-vivo spectroscopic quantitation, but also for specific MRI simulations involving selective excitation, coupled spin systems or relaxation. The software is available under a jMRUI license.Acknowledgements
The recent development has been supported by MEYS CR grants CZ.02.1.01/0.0/0.0/16_013/0001775, LO1212, and the EC Marie-Curie grant 316679 (TRANSACT).References
1. Z Starčuk Jr., J Starčuková, Analytical Biochemistry 529 (2017) 79-97 (and references within)
2. H Ratiney, M Sdika, Y Coenradie, S Cavassila, D van Ormondt, D Graveron-Demilly, NMR in Biomedicine, 18 (2005) 1-13
3. J-B Poullet, D M Sima, A W Simonetti, B De Neuter, Le Vanhamme, P Lemmerling, S Van Huffel, NMR in Biomedicine, 20 (2007), 493-504
4. S W Provencher, Magn. Reson. Med. 30 (1993) 672e679
5. D Graveron-Demilly, A Diop, A Briguet, B Fenet, J. Magn. Reson. Ser. A 101 (1993) 233e239,
6. S A Smith, T O Levante, B H Meier, R R Ernst, J. Magn. Reson. Ser. A 106 (1994) 75e105