Synopsis

An iterative reconstruction algorithm for sodium magnetic resonance imaging (²³Na MRI) with multi-channel receiver coils is implemented and compared to a conventional gridding reconstruction. Based on compressed sensing (CS) it utilizes a total variation (TV⁽²⁾), combined with anatomical weighting factors (AnaWeTV⁽²⁾) to preserve known tissue boundaries. Simulated and measured ²³Na multi-channel data sets of the female breast were reconstructed. The TV⁽²⁾ and in particular the AnaWeTV⁽²⁾ lead to an improved image quality, due to effective noise reduction and the highlighting of structure. The presented CS reconstruction is beneficial especially for high undersampling factors.

Introduction

Sodium magnetic resonance imaging (²³Na MRI) suffers from an inherently low signal-to-noise ratio, due to low in vivo concentrations, low MR sensitivity and short relaxation times. As a consequence, the spatial resolution is limited and image quality can be affected by partial volume effects or Gibbs ringing artifacts. Advanced image reconstruction methods, such as compressed sensing (CS) [1], can be used to overcome these restrictions and improve image quality. Based on that, we propose an iterative reconstruction algorithm for multi-channel data sets, which utilizes a total variation (TV⁽²⁾), adopted by weighting factors (AnaWeTV⁽²⁾) [2] to preserve known tissue boundaries. In this work, the AnaWeTV⁽²⁾ reconstruction is compared with a conventional TV⁽²⁾ and the gridding reconstruction [3] using simulated and measured ²³Na MRI multi-channel data of the female breast.

Methods

Reconstruction algorithm: The image reconstruction is done via a CS scheme [1]. Thereby the objective function

$$f(x)=\frac{1}{2} \left\|\textbf{A}x-y\right\|_2^2+\tau\sum\limits_{\alpha=x,y,z} \left( \lambda \left\|\textbf{W}_\alpha \textbf{D}_\alpha^{(1)}x\right\|_1+(1-\lambda) \left\|\textbf{W}_\alpha \textbf{D}_\alpha^{(2)}x\right\|_1 \right)$$

is minimized through an iterative algorithm that employs the conjugate gradient method. The first term ensures data consistency by calculating the difference between the raw data y and the current image x; the second term represents the second order total variation, which works as a conventional denoising technique, adopted by weighting factors W [2]. They are extracted from a high-resolution ¹H image by calculating the first derivation in each direction, and thus reduce the total variation at known tissue boundaries. Via τ parameter, the data consistency and the sparsity term can be weighed against each other; τ is optimized for each reconstructed channel and data set.

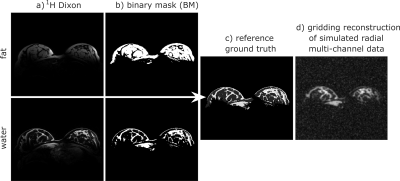
Simulations: Dixon ¹H measurements (FOV: 246x320x128 mm³, resolution: (1 mm)³, T_AQ = 1:46 min) are used to create a fat and water binary mask (BM) (Fig. 1a,b). The masks are added (1$$$\cdot$$$BM_fat + 6$$$\cdot$$$BM_water) to generate a high-resolution ground truth with a tissue contrast similar to that in a ²³Na image (Fig. 1c). By multiplying the ground truth with calculated sensitivity maps, a corresponding multi-channel ground truth is obtained. To reduce the spatial resolution to (3x3x1 mm³), high frequency k-space data is cut off, followed by a biexponential decay (T_2f^* = 2 ms, T_2s^* = 17 ms) and the regridding to a radial trajectory. Finally, synthetic correlated complex Gaussian noise is added.

The simulated data sets are used to test and optimize the algorithm. Results are compared to the existing ground truth (Fig. 1c). For this, the structural similarity (SSIM) [4] inside the object is calculated to assess the image quality; thereby a value of 1 corresponds to complete agreement between the reconstructed image and the ground truth.

Measurements: This study was approved by an institutional review board. In vivo MR measurements of a female healthy subject (age: 27) were carried out at a 7T whole-body system (Magnetom, Siemens Healthcare, Erlangen, Germany), using a dual-tuned proton/ sodium (¹H/ ²³Na) bilateral phased-array breast coil (Quality Electrodynamics, OH, USA). A density adapted 3D radial projection reconstruction pulse sequence (DA-3DRP) [5] was employed (TR/ TE = 30 ms/ 0.55 ms, FA = 67°, T_RO = 9.98 ms, FOV: 320 mm, nominal resolution: (3 mm)³), to carry out four ²³Na measurements with different undersampling factors (USFs):

• 20.000 projections, USF = 1.8
• 10.000 projections, USF = 3.6
• 5.000 projections, USF = 7.2
• 2.500 projections, USF = 14.4

Results

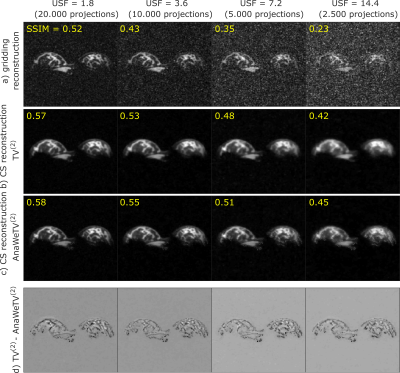
Fig. 2 depicts the results of reconstructed simulated data, combined via a sum-of-squares (SOS) reconstruction.
The use of a simple TV⁽²⁾ as sparsity transformation leads to better results compared with the conventional gridding reconstruction: the SSIM indicates an improved image quality, especially for high USFs (Fig. 2a,b).
The AnaWeTV⁽²⁾ compared with the TV⁽²⁾ as sparsity transformation preserves known tissue boundaries and improves the resolving of fine structures, both indicated by a higher SSIM value (Fig. 2c). This can also be comprehended by calculating the differences between the TV⁽²⁾ and the AnaWeTV⁽²⁾ reconstruction, where edges can be tracked systematically (Fig. 2d).
While the SSIM decreases quickly with higher USFs for the gridding reconstruction, it decreases significantly slower in the case of the CS reconstruction.

The reconstruction of measured data is in agreement with the results of simulations (Fig. 3).

Discussion and Conclusion

The presented CS algorithm leads to a significant improvement of image quality compared to the gridding reconstruction, due to the effective reduction of noise and imaging artifacts. Using the AnaWeTV⁽²⁾, known tissue boundaries are preserved, which leads to a further improvement. Especially for high USFs, the CS reconstruction shows a clear advantage over the gridding reconstruction. Using the presented algorithm the acquisition time can be reduced while image quality is preserved.

Acknowledgements

References