Synopsis

Magnetic resonance spectroscopy (MRS) is commonly converted from its free induction decay (FID) data with Fourier transform. How to reconstruct high quality spectra is one of the fundamental problems for MRS. In this work, a reconstruction method is proposed to explore the general exponential property of FID. Each exponential function of FID is explicitly enforced with the Hankel matrix Vandermonde Factorization (HVaF). This model is then applied to spectrum reconstruction of sparsely sampled FID in fast MRS. Results on synthetic and realistic MRS show that the new approach requires fewer data to allow successful reconstruction and provides better reconstruction on low-intensity signals than the state-of-the-art low rank Hankel matrix method. Thus, the new approach would be useful for faster data acquisition or recovery of weak spectral peaks in MRS applications.

Purpose

High quality spectra reconstruction from free induction decay (FID) data is one of the fundamental problems for magnetic resonance spectroscopy (MRS). Reconstruction is challenging when FID is highly undersampled for fast multidimensional MRS [1-5] that has important applications in studying a molecular structure and interactions of biopolymers in medical imaging, chemistry and biology. In this work, we explore the general exponential property of FID and explicitly constrain the signal space to be damped sinusoids with a proposed Vandermonde Factorization model. Results on synthetic and realistic MRS show that the new approach requires fewer data to allow successful reconstruction and provides better reconstruction of low-intensity signals than the state-of-the-art low rank Hankel matrix method [1].

Method

The general signal property in MRS that the FID can be approximated by a sum of several decaying exponentials has been widely acknowledged [1, 6-9]. Let vector $$${\bf{x}} \in {^{2N - 1}}$$$ be the complex FID $$x_{n}=\sum_{r=1}^{R}d_{r}e^{-n\Delta t/ \tau _{r}+i2\pi f_{r}n\Delta t} \qquad (1)$$ where $$${d_r}$$$, $$${\tau_r}$$$ and $$${f_r}$$$ are the complex amplitude, decay time and frequency, respectively, of the $$${r^{th}}$$$ exponential, and $$$R$$$ is the total number of exponentials, i.e. the number of spectral peaks. Let define $$$z_{r}=e^{-\Delta t/\tau _{r}+i2\pi f_{r}\Delta t}$$$, then the Hankel matrix of the FID admits a Vandermonde factorization $${{\cal H}}{\bf{x}} = \left[ {\begin{array}{*{20}{c}}1& \cdots &1\\{{z_1}}& \cdots &{{z_R}}\\ \vdots & \vdots & \vdots \\{z_1^{N - 1}}& \cdots &{z_R^{N - 1}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{d_1}}&{}&{}\\{}& \ddots &{}\\{}&{}&{{d_R}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1&{{z_1}}& \cdots &{z_1^{N - 1}}\\ \vdots & \vdots & \vdots & \vdots \\1&{{z_R}}& \cdots &{z_R^{N - 1}}\end{array}} \right] = {\bf{ZD}}{{\bf{Z}}^T} \qquad (2)$$ where $$${\cal H}$$$ denotes an operator that tranformsa vector into a square Hankel matrix.

An advantage of this specific factorization is that each column in the matrix $$${\bf{Z}}$$$ in Eq. (2) carries an explicitly single exponential function information, including the central frequency and damping factor. Besides, the second matrix, $$${\bf{D}}$$$, will be low rank if a larger Hankel matrix is constructed as it was done in the existing low rank Hankel matrix methods [1]. Vandermonde factorization explicitly constrains the signal space of FID to be composed of exponential functions, thus provides more physical meaning of FID than the LRHM [1].

In this work, we propose to factorize the Hankel matrix into two Vandermonde matrices, $$${\bf{U}}$$$ and $$${\bf{V}}$$$ , and further constraint each column of Vandermonde matrices to be one exponential function, which the is relaxed with a nuclear norm minimization. The overall signal reconstruction model is named as Hankel matrix completion with Vandermonde Factorization (HVaF) $$\begin{array}{c}\mathop {\min }\limits_{{\bf{U}},{\bf{V}},{\bf{y}}} \sum\limits_{r = 1}^\hat R {\left( {{{\left\| {{{\cal R}}{{{\cal Q}}_r}{\bf{U}}} \right\|}_*} + {{\left\| {{{\cal R}}{{{\cal Q}}_r}{\bf{V}}} \right\|}_*}} \right) + \frac{\lambda }{2}\left\| {{\bf{g}} - {\bf{Cy}}} \right\|_2^2} \\s.t.{\kern 1pt} {\kern 1pt} {{\cal H}}{\bf{y}} = {\bf{U}}{{\bf{V}}^H}\end{array} \qquad (3)$$ where $$$\bf{g}$$$ is the sparsely sampled data under a sampling operator $$$\bf{C}$$$, $$${\cal Q}_r$$$ gets the $$${r^{th}}$$$ column of the matrix and $$${\cal R}$$$ converts a vector into Hankel matrix, $$$\hat R$$$ is the estimated number of peaks that is set as $$$\hat R = 10R$$$.

Results

We verify the methods on both synthetic and realistic MRS data. The proposed HVaF is compared with the state-of-the-art LRHM [1].

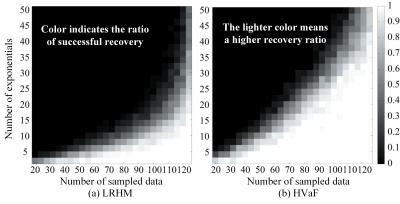
Results on the synthetic data are shown in Fig. 1. Synthetic data are generated according Eq. (1) and $$$M$$$ data points are sampled uniformly at random. For each $$$\left( {R,M} \right)$$$ pair, 100 Monte Carlo trials are conducted. Each trial is declared successful if $$$\frac{{\left\| {{\bf{y}} - {\bf{x}}} \right\|}}{{\left\| {\bf{x}} \right\|}} \le {10^{ - 3}}$$$, where $$${\bf{x}}$$$ and $$${\bf{y}}$$$ are the true and reconstructed FID, respectively. The successful recovery ratio shown in Fig.1 indicates that HVaF requires a smaller number of measurements for successful reconstruction than the LRHM.

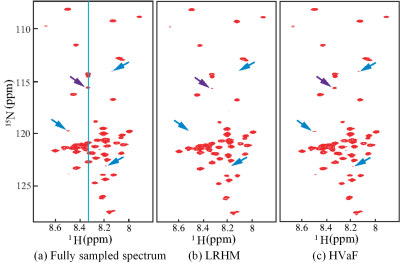
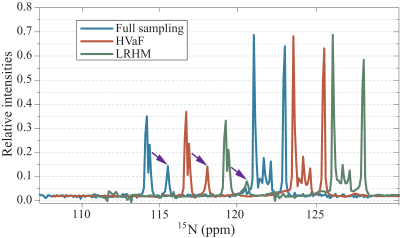
Results on the 2D 1H-15N HSQC data are shown in Fig. 2. This data are acquired on the intrinsically disordered cytosolic domain of human CD79b protein from the B-cell receptor [1] and 17% FID data in the indirect dimension are acquired following Poisson-gap undersampling [10]. Fig. 2 shows that HVaF achieves a reliable reconstruction while LRHM seriously distorts or even loses some weak peaks. Fig. 3 further illustrates that several low-intensity peaks are notably compromised in the LRHM spectrum, while HVaF succeeds to recover them.

Conclusion

Acknowledgements

This work was partially supported by National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61571380, 61302174 and U1632274), Fundamental Research Funds for the Central Universities (20720150109) and Natural Science Foundation of Fujian Province of China (2016J05205). The authors thank Vladislav and Maxim for sharing the MRS data used in this work.

The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)

References

1. X. Qu, M. Mayzel, J. F. Cai, Z. Chen, and V. Orekhov, Accelerated NMR spectroscopy with low-rank reconstruction, Angewandte Chemie International Edition, 54:852-854, 2015.

2. X. Qu, X. Cao, D. Guo, and Z. Chen, Compressed sensing for sparse magnetic resonance spectroscopy, ISMRM 2010, 3371.

3. X. Qu, D. Guo, X. Cao, S. Cai, and Z. Chen, Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension, Sensors, 11:8888-8909, 2011.

4. K. Kazimierczuk and V. Y. Orekhov, Accelerated NMR spectroscopy by using compressed sensing, Angewandte Chemie International Edition, 50:5556-5559, 2011.

5. D. J. Holland, M. J. Bostock, L. F. Gladden, and D. Nietlispach, Fast multidimensional NMR spectroscopy using compressed sensing, Angewandte Chemie International Edition, 50:6548-6551, 2011.

6. J. C. Hoch and A. S. Stern, NMR data processing: Wiley-Liss, 1996.

7. H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy, IEEE Transactions on Biomedical Engineering, DOI:10.1109/TBME.2017.2719709, 2017.

8. J. Ying, H. Lu, Q. Wei, J. F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, Hankel matrix nuclear norm regularized tensor completion for $N$-dimensional exponential signals, IEEE Transactions on Signal Processing, 65:3702-371, 2017.

9. H. M. Nguyen, X, Peng, M. N. Do, and Z.-P. Liang, Denoising MR spectroscopic imaging data with low-rank approximations, IEEE Transactions on Biomedical Engineering, 60:78-89, 2013.

10. S. G. Hyberts, K. Takeuchi, and G. Wagner, Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data," Journal of the American Chemical Society, 132:2145-2147, 2010.