1288

Optimized Crusher Design for Magnetic Resonance Spectroscopy
Karl Landheer1 and Christoph Juchem1,2

1Biomedical Engineering, Columbia University, New York, NY, United States, 2Radiology, Columbia University, New York, NY, United States

Synopsis

Modern magnetic resonance spectroscopic (MRS) pulse sequences frequently overlook the issue of unwanted coherence pathways. A novel and robust algorithm which only requires input of the desired coherence(s) was developed to optimally crush all unwanted coherence pathways for any MRS pulse sequence. Experiments were performed on the GE BRAINO phantom comparing crusher schemes obtained from the literature with those obtained from the developed optimization algorithm for sLASER and MEGA-sLASER. The results demonstrate that the effects of unwanted coherences can be drastically reduced through the implementation of an optimized crusher scheme, without the need for additional or stronger crushers.

Introduction

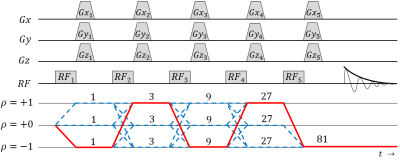
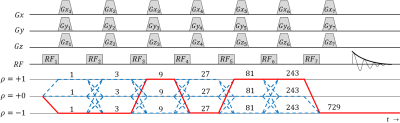
In a magnetic resonance spectroscopy (MRS) pulse sequence a scheme of pulsed magnetic field gradient "crushers" are played out during times in-between radiofrequency (RF) pulses to dephase unwanted coherence pathways which are incidentally perturbed by the RF pulses. Figure 1 and Figure 2 are pulse sequence and coherence pathway diagrams employing 5 and 7 RF pulses, respectively. The number of measured coherence pathways with maximum coherence order of 1 can be expressed by $$$3^{n-1}$$$, where n is the number of RF pulses. The number of unwanted coherences is therefore largely increased for modern sequences such as LASER [1], sLASER [2] or MEGA-sLASER [3] over three-pulse experiments and the challenge of designing an appropriate crusher scheme becomes more difficult. A strategy for designing a crusher scheme is to adjust crusher areas until the experimentally measured spectrum appears free from the typical unwanted pathway characteristics, however unwanted pathways can be easily overlooked. As such there can be found examples in the literature of MRS sequences which do not crush all unwanted pathways, for example the crusher schemes used by Landheer [4], Scheenen [5], Prinsen [6], and Andreychenko [3] do not crush 1, 26, 8 and 8 of the 8, 242, 728 and 728 unwanted coherence pathways, respectively. Here we present a fully automated algorithm, which requires no experimental iteration, for the design of optimal crusher schemes for MRS sequences, as well as its application to modern MRS sequences (sLASER and MEGA-sLASER).

Methods

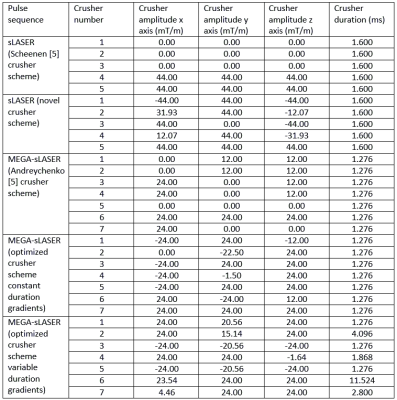
A vector of the crushing strength, $$$D$$$, or the “impact” of the crusher gradients can be expressed as $$D = \sqrt{(XA)\cdot (XA)},$$ where $$$X$$$ is a matrix of size 3 by n that describes the area of the n individual crusher gradients along the three orthogonal axes and $$$A$$$ is a matrix which describes all of the possible coherence pathways for the n-pulse experiment. The vector of crushing strength for all unwanted pathways, $$$\tilde D$$$, is then created which is identical to $$$D$$$ except that it has the row(s) corresponding to the desired coherence pathway(s) removed, as well as all pathways which do not end with a -1 coherence order, as it is the only coherence order directly measured with quadrature detection [7]. The optimal crusher area scheme, $$$\hat X$$$ is then calculated according to the equation$$\hat X = argmax_x(min(\tilde D) + mean(\tilde D)),$$ subject to the constraints that the crushing strength must be zero for the coherence pathway(s) of interest and the gradient areas must be within the physical limits. This optimization was achieved using the active set method as implemented in MATLAB (Mathworks, Natick, MA), using a random set of initial crushers and repeated 10,000 times in order to ensure convergence to a global maximum. We investigated the effect of crusher schemes from the literature and our optimized crusher schemes on the MRS spectral appearance. The schemes for sLASER and MEGA-sLASER obtained from the literature were from [5] and [3], respectively. The experimental values for the crusher duration and amplitude are shown in Table 1. All experiments were performed on a MR750 3T MRI system (GE Healthcare, WI, USA) at the New York State Psychiatric Institute with a standard eight-channel head coil receiver. Echo times of 40 ms for sLASER and 72 ms for MEGA-sLASER were used. Experiments were performed on the GE BRAINO phantom with receiver bandwidth of 2500 Hz, 2048 acquired points, TR of 1500 ms, 128 excitations and a voxel size of 20x20x20 $$$mm^3$$$.

Results

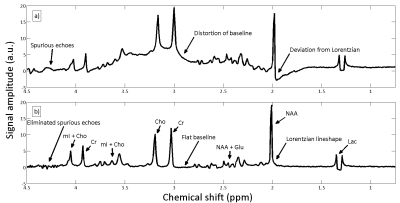
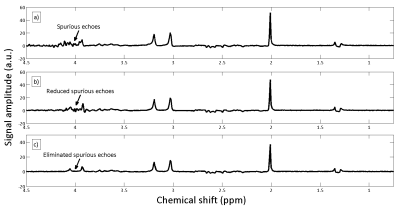
The acquired spectra for both crusher schemes for sLASER and MEGA-sLASER are displayed in Figure 3 and Figure 4, respectively. As can be readily seen from Figure 3a) there is substantial baseline distortion for the crusher scheme from the literature (consistent with published results [5]) as well as distortions of the lineshapes, which are completely removed by modifying the crusher's amplitude distribution, as shown in Figure 3b). For MEGA-sLASER there are noticeable spurious echoes in Figure 4a), which are lessened by using the optimal crusher scheme as shown in Figure 4b), and negligible when using the variable-length crushing scheme as shown in Figure 4c).

Discussion

The results presented here demonstrate that the effects of unwanted coherences can be drastically reduced through the implementation of an optimized crusher scheme in a phantom. Furthermore, a proper crushing scheme is more important for in vivo experiments because the increased B1 inhomogeneity results in an increased probability for unwanted coherence transitions. A novel and robust algorithm was developed to optimally crush all unwanted coherences for any MRS pulse sequence, and was demonstrated experimentally in sLASER and MEGA-sLASER.

Acknowledgements

Special thanks to the New York State Psychiatric Institute for all their support.

References

1. Garwood, M. & DelaBarre, L. The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR. J. Magn. Reson. 153, 155–177 (2001).

2. Scheenen, T. W., Heerschap, A. & Klomp, D. W. Towards 1H-MRSI of the human brain at 7T with slice-selective adiabatic refocusing pulses. MAGMA 21, 95–101 (2008).

3. Andreychenko, A., Boer, V. O., Arteaga de Castro, C. S., Luijten, P. R. & Klomp, D. W. J. Efficient Spectral Editing at 7 T: GABA Detection with MEGA-sLASER. Magn Reson Med 68, 1018–1025 (2012).

4. Landheer, K., Sahgal, A., Das, S. & Graham, S. J. Constrained Source Space MR Spectroscopy: Multiple Voxels, No Gradient Readout. Am J Neuroradiol 37, 1–8 (2015).

5. Scheenen, T. W. J., Klomp, D. W. J., Wijnen, J. P. & Heerschap, A. Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magn Reson Med 59, 1–6 (2008).

6. Prinsen, H., de Graaf, R. a, Mason, G. F., Pelletier, D. & Juchem, C. Reproducibility measurement of glutathione, GABA, and glutamate: Towards in vivo neurochemical profiling of multiple sclerosis with MR spectroscopy at 7T. J Magn Reson Imag 45, 187–198 (2017).

7. Mitschang, L., Ponstingl, H., Grindrod, D. & Oschkinat, H. Geometrical representation of coherence transfer selection by pulsed field gradients in high-resolution nuclear magnetic resonance. J. Chem. Phys. 102, 3089–3098 (1995).

Figures

Figure 1: Coherence pathway diagram for five RF pulses with a maximum coherence order (ρ) of 1. RF pulses induce transitions between the coherence order, and the coherence order history prior to detection represents the coherence pathway. The desired coherence pathway for sLASER is shown in red, all other coherence pathways are depicted as dashed blue lines. In general there is substantial overlap at each step in the coherence pathway, thus the total number of distinct but overlapping pathways are indicated. A properly designed crusher scheme sufficiently dephases all unwanted coherence pathways while leaving the desired coherence pathway(s) unaffected.

Figure 2: Coherence pathway diagram for seven RF pulses with a maximum coherence order (ρ) of 1. The desired coherence pathway for MEGA-sLASER is shown in red, all other coherence pathways are shown as dashed blue lines. The number of overlapping individual coherence pathways are indicated. $$$RF_2$$$ and $$$RF_6$$$ are frequency-selective pulses which do not directly perturb the measured magnetization.

Table 1: Crusher duration and amplitude for sLASER and MEGA-sLASER experiment shown in Figures 3 and 4, respectively. The crusher number corresponds to the labels as shown in Figures 1 and 2. The durations of all crushers along all three of the individual orientation axes have been set to be equal.

Figure 3: sLASER spectra from BRAINO phantom with TE = 40 ms using a crusher scheme obtained from a) Scheenen [5] and b) the novel crusher scheme from the developed algorithm with crushers that have equal maximum amplitude and duration. As can be seen the spurious echoes substantially distort the baseline and quality of the spectra, which can be drastically reduced by only modifying the crusher scheme without changing the individual crusher duration or maximum amplitude. The amplitude and duration of all crushers used are given in Table 1.

Figure 4: MEGA-sLASER spectra from BRAINO phantom with TE = 72 ms using a crusher scheme obtained from a) Andreychenko [3], b) the optimized crusher scheme with crushers that have equal maximum amplitude and duration and c) the optimized crusher scheme with crusher durations matched to the time between successive RF pulses. The amplitude and duration of all crushers used are given in Table 1. There is a reduction in signal amplitude for the novel crusher scheme, particularly c), due to the increased diffusion weighting.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1288