1230

Scan parameter optimization of dual-venc 4D Flow MRI for the assessment of neurovascular flow networks in brain arteriovenous malformation
Maria Aristova1, Alireza Vali2, Alex Barker2, Ali Shaibani3, Sameer Ansari4, Matthew Potts5, Babak Jahromi5, Michael Hurley4, Susanne Schnell2, and Michael Markl2

1Biomedical Engineering, Northwestern University, Chicago, IL, United States, 2Radiology, Northwestern University, Chicago, IL, United States, 3Radiology, Neurosurgery, Northwestern University, Chicago, IL, United States, 4Neurointerventional radiology, Northwestern University, Chicago, IL, United States, 5Neurosurgery, Northwestern University, Chicago, IL, United States

Synopsis

To optimize dual-venc 4D Flow MRI parameters for flow assessment in brain arteriovenous malformations, we conducted an in-vitro optimization analysis and compared it to in-vivo data from a patient with complex AVM. Using k-t acceleration factors of 2-5 and about 2-10 voxels across the imaged vessels, we quantified the agreement with the ground truth flow and geometry. We applied a flow distribution network graph concept to characterize flow conservation as an additional quality metric. Data indicated that approximately 5 voxels across imaged vessels are needed, consistent with results from previous publications.

Introduction

Dual-venc 4D Flow MRI1 requires trade-offs between spatial resolution, temporal resolution, field of view (FOV) and acceleration, where optimal parameter combinations are highly application-dependent. Dual-venc 4D Flow MRI uses two velocity encodings (low and high venc) within one acquisition to achieve a large dynamic velocity range and velocity to noise ratio. Hemodynamic characterization of brain arteriovenous malformations (AVM) requires the large dynamic velocity range and VNR of dual-venc, large FOV and high spatial and temporal resolution, for accurate flow quantification in the main arteries and veins, which can be as small as 3mm. Previous work2 established minimum 4-5 voxels across a vessel for accurate quantification, but at 3T and with dual-venc, this guideline merits further exploration. We applied kt-accelerated, dual-venc 4D Flow in-vitro with known steady flow in a branched network of parallel flow channels, and explored the parameter space of spatial resolution and k-t acceleration factor to identify 4D Flow scan parameters enabling flow quantification within 10% of ground truth, and internal flow conservation within 10%. In this context, we present hemodynamic metrics and flow network analysis of a complex AVM.

Methods

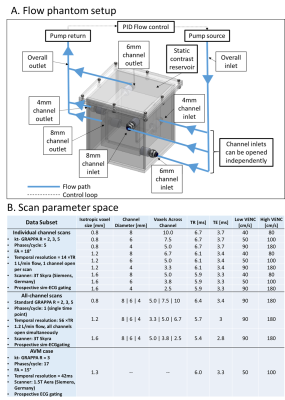
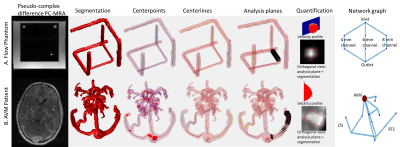
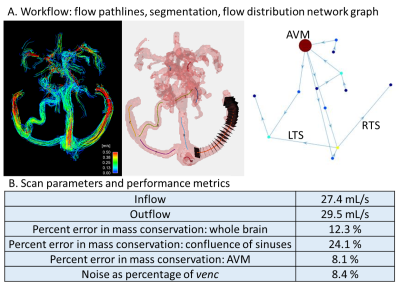
An in-vitro flow phantom contained flow along all spatial dimensions in 4, 6 and 8mm diameter channels (Fig.1). Water with 2mM gadolinium (Ernst angle3 =18°) circulated via a steady flow pump (Micropump, USA) and was also used to fill the phantom shell as a static eddy current correction reference. Total inlet flow was regulated via PID feedback control implemented in LabView (National Instruments, USA) and a flow meter (OMEGA, USA). The phantom was imaged at 3T (Skyra: Siemens, Germany) using dual-venc 4D Flow MRI with high-venc values set to avoid velocity aliasing (settings: Fig.1B). Using in-house-developed software (Fig.2), data were corrected for phase offset errors and noise. A phase-contrast angiogram was calculated and segmented. ~20 analysis planes/vessel segment were used to obtain velocity profile, net flow and vessel diameter. Flow distribution network graphs (FDNG: Fig.2) were constructed, tracking vessel connectivity and flow conservation. For each spatial resolution and acceleration factor combination, we computed net flow and diameter measurement error from known values, static tissue velocity noise, and flow network mass conservation. The methods were applied to a patient with complex bithalamic AVM (female-10yo: Fig.1B), imaged at 1.5T (Aera: Siemens, Germany). Velocity noise and flow conservation were characterized and a FDNG was extracted (Fig.2B).

Results and Discussion

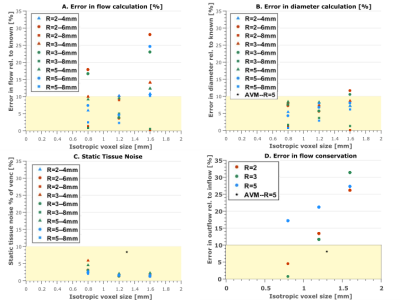
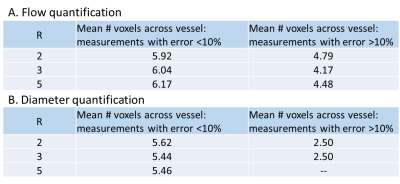
Results indicate complex interactions between acceleration factor, spatial resolution and number of voxels across the imaged vessel, which all impact the overall image quality and quantification accuracy. Percent flow quantification error (Fig.3A) depends on all these factors. For (1.2mm)3 resolution at all R, the error is <10%, potentially balancing noise (more significant at higher resolution) and partial volume effects (more significant at lower resolution). Scan conditions with <10% error have >5 voxels across each vessel at all R (Fig.4A), consistent with previous findings. However, the resolution appears to dominate over the number of voxels across a vessel. Evaluating the impact of this metric likely requires a more finely differentiated scan parameter space.

Both of the scans with >10% quantification error in vessel diameter measurement had 2.5 voxels across the vessel (6mm channel at (1.2mm)3 resolution, R=2 and R=3 respectively: Fig.3B and 4B). Velocity noise in static tissue (Fig.3C) was <5% for all but one in-vitro measurement (R=3 and 5 voxels across the vessel), but ~8% in-vivo, potentially due to less accurate static tissue identification in-vivo, patient motion, or lower field strength.

In FDNG analysis of in-vitro scans of the entire branched phantom system (Fig.3D), flow conservation error increases monotonically with decreasing spatial resolution. More accelerated scans have higher mass conservation error, but less sensitivity to voxel size. Both scans with <10% flow conservation error ((0.8mm)3 spatial resolution, R=2 and R=3 respectively), have ≥5 voxels across each vessel, consistent with results of flow quantification accuracy. In-vivo data for flow conservation across the AVM (8.4% error) met the 10% flow conservation error benchmark despite being collected at R=5; however, flow conservation error across the confluence of sinuses and whole brain was higher, suggesting a need for further exploration of these metrics in-vivo, particularly in the venous system.

Conclusions

Results suggest an optimal spatial resolution, (1.2mm)3 and a minimal number of 5 voxels across the vessel to minimize noise and maximize quantification accuracy and consistency. Broadly, in-vivo data aligns with in-vitro results and indicates dual-venc 4D flow applications in AVM are feasible. However, more refined exploration of this parameter space is needed. Future work will consider impact of temporal resolution for pulsatile flow.

Acknowledgements

We gratefully acknowledge funding from the following sources: AHA Scientist Development Grant 16SDG30420005, NIH K25HL119608 and NIH R01HL115828.

References

1. Schnell S, S.A. Ansari, C. Wu, J. Garcia, I.G. Murphy, O.A. Rahman, A.A. Rahsepar, M. Aristova, J.D. Collins, J.C. Carr, M Markl. Accelerated dual-venc 4D flow MRI for neurovascular applications. JMRI 2017; 46:102–114.

2. Dyverfeldt P, M. Bissell, A.J. Barker, A.F. Bolger, C.J. Carlhäll, T. Ebbers, C.J. Francios, A.Frydrychowicz, J. Geiger, D.l Giese, M.D. Hope, P. J. Kilner, S. Kozerke, S. Myerson, S. Neubauer, O.Wieben and M. Markl. 4D flow cardiovascular magnetic resonance consensus statement. JCMRI 2015;17:72.

3. Sasaki M, Shibata E, Kanbara Y, Ehara S. Enhancement effects and relaxivities of gadolinium-DTPA at 1.5 versus 3 Tesla: a phantom study. Magn Reson Med Sci. 2005; 4(3):145-9.

Figures

(A) Schematic of 3D-printed flow phantom: each channel (4, 6, 8mm) contains flow in 3 consecutive, orthogonal segments of identical length between inlet and outlet. Emulating branched AVM flow networks, inlets to all channels are fed by branches of one flexible hose (pump source) outside imaged volume; channel outlets are similarly linked (pump return). (B) In-vitro and in-vivo parameters: phantom flow channels were scanned individually at 1L/min flow using a precise flowmeter, then together at approximately 1.2L/min total flow. R=2, 3, 5 and isotropic spatial resolution (0.8mm)3, (1.2mm)3 and (1.6mm)3 were used, for a range of 2-10 voxels across vessel.

Workflow for (A) in-vitro and (B) in-vivo scans: Preprocessing (noise and phase offset correction, generation of pseudo-complex difference PC-MRA), automated quantification (segmentation, centerpoint and centerline extraction, analysis plane placement (every 4mm in each vessel segment) with velocity profile, quantification), representation in flow distribution network diagram (FDNG). The FDNG is a mechanism for internal representation of vessel connectivity in the data, which allows for straightforward computation of flow conservation across an arbitrary vessel junction or the whole brain. FDNG in (B) shows AVM, left transverse sinus (LTS) and right transverse sinus (RTS).

Sensitivity analysis for (A) flow measurement error, (B) diameter measurement error, (C) static tissue velocity noise as percentage of low venc, and (D) error in mass conservation across the entire volume, i.e. relative error of outflow vs. inflow, for each value of GRAPPA R and spatial resolution. Data with 10% error or less are highlighted in each case. (C) and (D) include the corresponding metric for in-vivo AVM data.

Comparison of voxel numbers across vessel diameter to achieve accuracy in (A) flow and (B) diameter quantification within 10%. Only two measurements showed diameter quantification error over 10%: (1.6mm)3 resolution in 6mm channel at R=2 and R=3.

AVM case: (A) Workflow, including visualization of flow streamlines, PC-MRA segmentation and plane placement along the right transverse sinus, and FDNG, which is a comprehensive representation of flow metrics and vessel connectivity in complex flow networks such as AVM. Flow quantification is interpolated based on recorded pulse rate. (B) Performance metrics for this scan, including flow conservation error across confluence of sinuses, AVM and whole brain.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1230