1209
Estimating susceptibility-induced field changes directly from diffusion MRI images and overcoming associated computational bottlenecks through GPU parallelisation1FMRIB, Wellcome Centre for Integrative Neuroimaging, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Centre for Medical Image Computing & Department of Computer Science, University College London, London, United Kingdom
Synopsis
We present a novel method (incorporated into FSL $$$\texttt{eddy}$$$) of estimating and correcting distortions due to dynamic changes in the susceptibility field when measuring diffusion using EPI. This method is able to track how the field changes with movement using only the diffusion data itself. We demonstrate an improvement in distortion correction, compared to using a static susceptibility field, for both simulated and actual data. Additionally, we demonstrate how computationally intensive portions of the estimation algorithm can be speeded up through GPU parallelisation. Reducing the runtime increases the likelihood of this method being widely adopted and broadens its impact potential.
Introduction
Susceptibility-induced distortions are problematic when measuring diffusion using Echo-Planar Imaging (EPI). This is typically addressed using a map of the susceptibility field, acquired along with the diffusion scan, and is predicated on the assumption that the field does not change with time. Subject movement violates that assumption, and a single fieldmap can no longer account for distortion changes during the experiment1. We present a method (incorporated into FSL $$$\texttt{eddy}$$$2) that is able to track field changes as a consequence of movement using only the diffusion data itself. Additionally, we demonstrate how the estimation can be speeded up using Graphical Processing Units (GPUs).Theory
When a subject's head moves in the scanner, the susceptibility field will, to a first approximation, follow the subject. But for larger movements, particularly rotations around any axis non-parallel to the magnetic flux, that approximation becomes increasingly poor. We suggest (figure 1) modelling the changing field as a first order Taylor expansion with respect to rotation around the x-axis (pitch) and y-axis (roll). This reduces the problem from estimating a field per volume to estimating two "derivative fields", where each voxel encodes the rate of change of the field with respect to rotation. A forward model was proposed to predict the signal change in each voxel, given derivative fields with respect to pitch and roll. From this we derived an inverse model (figure 2) for estimating the derivative fields from the observed volume-to-volume changes in voxelwise intensity.
The inverse model makes use of a very large, sparse matrix $$$\mathbf{X}^T\mathbf{X}$$$ which must be estimated multiple times. This is computationally expensive, but can be divided into multiple independent computations for each value. By parallelising these calculations, the single instruction, multiple data paradigm central to GPU operation was leveraged to overcome this bottleneck3.
Experiments
The method was validated using both simulations and experimental data. The simulations (where the true field and diffusion image are known) were performed using a highly realistic MRI simulator that was recently extended to include a model for how the susceptibility-induced field changes with subject movement4.
The experimental data consisted of a full diffusion scan on a trained and motivated subject. They remained absolutely still during one scan, followed by an identical scan where they moved at intervals of ~ten volumes. Here the diffusion weighted volumes from the "still" scan were considered ground truth when comparing the corrected images from the "movement" scan.
For both sets of data a static field was estimated from a pair of b0 images with reversed phase-encoding using FSL $$$\texttt{topup}$$$5. The static fields were passed, along with the data, to FSL $$$\texttt{eddy}$$$ to estimate subject movement and eddy currents. The method described here was incorporated into $$$\texttt{eddy}$$$ and the data, estimated for everything except the dynamic susceptibility field, was used as $$$\mathbf{f}$$$ and the Gaussian Process predictions as $$$\breve{\mathbf{s}}$$$ in figure 2. Movement estimates from $$$\texttt{eddy}$$$ were used as $$$\Delta\theta$$$ and $$$\Delta\phi$$$.
Special consideration was given to how data used during calculations was stored and accessed by the GPU. Only by ensuring that simultaneously executing threads acted on contiguous areas of memory, could the full benefits of the GPU be realised.Results
For both simulated and human data the estimated derivative fields looked very reasonable, with a high degree of left-right symmetry and anti-symmetry with respect to pitch and roll respectively6. Figure 3 demonstrates that the derivative fields estimated from the simulated data showed a high degree of similarity to the true derivative fields. Figure 4 shows the that the correlation with ground truth was vastly improved when performing the dynamic susceptibility correction compared to just using a static field.
Runtime for calculating $$$\mathbf{X}^T\mathbf{X}$$$ was approximately 30x faster for the GPU over the CPU implementation. Figure 5 shows that this result should hold for a wide range of B-spline parameterisations and volume resolutions.
Discussion
The results clearly show that we are able to estimate and correct for a susceptibility field that changes dynamically as a consequence of subject movement.
The GPU performance presented is for a fairly low-end unit (GeForce GT 750M). As each value in $$$\mathbf{X}^T\mathbf{X}$$$ in calculated by an independent thread on the GPU, performance should increase even further if run on a high-end device capable of executing more threads concurrently.
Conclusion
Our new method for estimating and correcting dynamic changes in susceptibility has the potential to improve the results of diffusion scans on subjects with an impaired ability to remain motionless. Adding GPU acceleration greatly increases the speed of this method, and should allow it to create a bigger impact in clinical use.Acknowledgements
The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). We also gratefully acknowledge the support from the Wellcome Trust Strategic Award 098369/Z/12/Z (J.A.), the NIH Human Connectome Project (1U01MH109589-01 and 1U01AG052564-01, J.A.), EPSRC grant EP/L504889/1 (M.G.) and the EPSRC Centre for Doctoral Training (EP/L016478/1, M.G.).References
1. Andersson J, Hutton C, Ashburner J, Turner R, Friston K. Modelling Geometric Deformations in EPI Time Series. NeuroImage. 2001;13:903-919.
2. Anderson J, Sotiropoulos S. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063-1078.
3. NVIDIA. CUDA C Programming Guide. September 22, 2017. http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html. Accessed November 7, 2017.
4. Graham M, Drobnjak I, Jenkinson M, Zhang H. Quantitative assessment of the susceptibility artefact and its interaction with motion in diffusion MR. PLOS ONE. 2017.
5. Anderson J, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20:870-888.
6. Sulikowska A. Motion correction in high-field MRI. PhD Thesis. University of Nottingham. 2016.
Figures


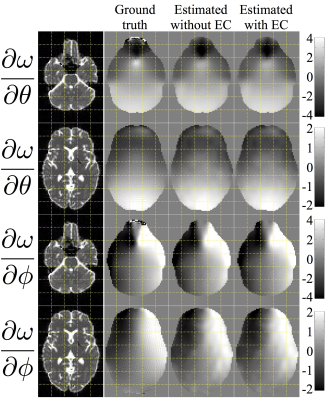
The leftmost column shows b0 images (of simulated data) for anatomical reference. The second column shows the true rate of change of the field with respect to pitch ($$$\theta$$$) and roll ($$$\phi$$$). Columns three and four show the estimated derivative fields with and without simultaneous estimation of eddy current. The units for the derivative maps are Hz/degree.
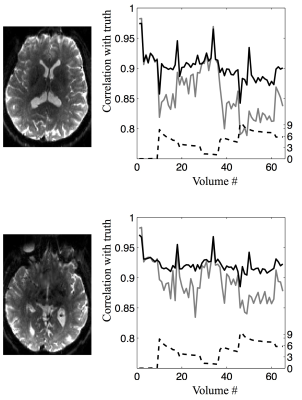
The left column shows b0 images (of data acquired on a human subject) for anatomical reference. In the second column the dashed line is a "movement index" incorporating both pitch and roll. The solid lines show the correlation, for each volume, with the corresponding "ground truth" volume when correcting using a single static field (grey solid line) and when performing the dynamic correction outlined in the present abstract (black solid line).
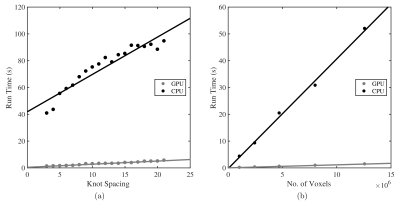
GPU and CPU performance for calculation of a $$$\mathbf{X}^T\mathbf{X}$$$ matrix, such as that in figure 2. (a) shows how runtime varies with cubic B-spline knot spacing for a volume of fixed resolution. Runtime increases approximately linearly for both implementations, with in the region of 30x better performance by GPU over CPU. (b) shows how runtime varies with volume resolution, whilst keeping knot spacing constant (here 4). Again, the GPU maintains its advantage over the CPU, with both implementations scaling linearly. This should facilitate the ease of adoption of this method by significantly reducing the required execution time.