1208
Higher order spherical harmonics reconstruction of fetal diffusion MRI with intensity correction1Biomedical Engineering, King's College London, London, United Kingdom, 2Perinatal Imaging and Health, King's College London, London, United Kingdom
Synopsis
We present a comprehensive method for reconstruction of fetal dMRI signal using a higher order spherical harmonics representation. We show that intensity correction improves the consistency of the volumetric reconstruction. By applying constrained spherical deconvolution and whole brain tractography to reconstructed fetal dMRI we are able to identify anatomically plausible fiber crossings.
Purpose
Acquisition of fetal MRI is complicated by fetal motion and maternal breathing. Echo planar imaging (EPI) used for diffusion MRI (dMRI) is acquired one slice at a time, and therefore motion corruption of the acquired data can be mostly avoided. The slices, however, need to be co-registered and resulting scattered data need to be reconstructed to produce consistent volumes on a regular grid1,2,3. We have previously proposed to perform the scatter data reconstruction using a super-resolution spherical harmonics (SH) approach4, which allows for higher order connectivity reconstructions5. In this work we show that given sufficient angular resolution and b-value, we are able to fit a 4th order SH model to fetal dMRI signals and identify anatomically plausible fiber crossings. We also show that intensity artefacts such as B1 inhomogeneity and motion induced spin history effects need to be corrected to obtain consistent reconstructions.Method
Our aim is to estimate SH representation $$$C$$$ of fetal dMRI signal $$$\overline{s}$$$ on a high-resolution isotropic grid represented by index $$$i$$$ $$\overline{s}_i(\overrightarrow{g})=\sum_{lm}c_{i,lm}Y_{lm}(\overrightarrow{g})$$ where $$$\overrightarrow{g}$$$ represents diffusion direction, $$$c_{i,lm}$$$ stand for SH coefficients and $$$Y_{lm}$$$ are real SH basis functions of order $$$m$$$. We denote the acquired image domain signal $$$s_{jk}$$$, where index $$$k$$$ represents a slice with associated diffusion direction $$$\overrightarrow{g}_k$$$ and $$$j$$$ represents an in-plane grid point of a slice. The forward model for simulation $$$ \overline{s}_{jk}$$$ of the acquired slices utilises the point spread function $$$m_{ij}^k$$$ which takes into account in-plane resolution, slice thickness, position and orientation of the fetal head in the scanner space at the time of acquisition6. Intensity effects such as B1 inhomogeneity and spin history are represented by slowly varying multiplicative factor $$$b_{jk}$$$: $$\overline{s}_{jk}=\sum_ib_{jk}m_{ij}^k\overline{s}_i(\overrightarrow{g}_k)$$ The SH representation $$$C$$$ is estimated by minimising the objective function $$$F(C,B)=\sum_{jk}(s_{jk}-\overline{s}_{jk})^2+R(B)$$$ where $$$R$$$ represents regularisation term to impose smoothness on the multiplicative field $$$B=(b_{jk})_{jk}$$$.
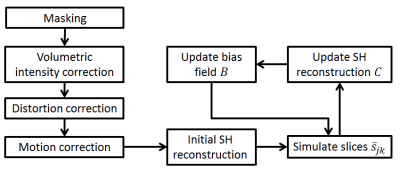
Diffusion MRI of three fetal subjects, gestational age (GA) 32, 33 and 35 weeks, were acquired on 3T Phillips Achieva scanner using spin echo EPI sequence (b=750 smm2, 32 directions, 3 volumes b=0 smm2, TE 75ms, TR 7500ms, voxel size 2x2x3.5mm3, slice overlap 1.75mm). The dataset was masked to exclude maternal anatomy and the bulk B1 intensity shading was corrected by applying a method previously proposed for fetal fMRI7 to the b=0 volumes. The susceptibility induced distortion was corrected by Laplacian constrained registration of b=0 volumes to ssFSE T2w images of the same subject8. Motion was corrected by slice to volume registration6 applied to all b=750 slices irrespective of the diffusion directions2. The SH representation $$$C$$$ and multiplicative bias field $$$B$$$ were estimated by minimising $$$F$$$ using gradient descent (GD) and regularisation was implemented by Gaussian blurring ($$$\sigma=20$$$) of $$$B$$$ after each GD iteration. The processing pipeline is summarised in Fig. 1.
Results
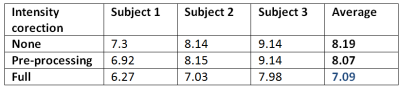
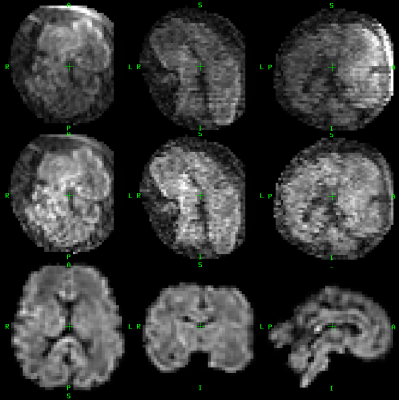
As this method extends our previously proposed framework6 by including the intensity correction in form of multiplicative field $$$B$$$, we evaluate the impact of including intensity correction only. We reconstructed the 4th order SH representation $$$C$$$ for each fetal subject using 27 diffusion volumes. Subsequently we simulated the diffusion data of the remaining 5 volumes using the forward model. These simulated volumes were compared to acquired data by calculating a root mean square error (RMSE). We evaluated RMSE for reconstructions with no intensity correction, volumetric intensity correction in the pre-processing stage and full slice-wise intensity correction during reconstruction. Table 1 shows that intensity correction improves data consistency as measured by RMSE for each subject. Figure 2 compares a single acquired volume, intensity corrected volume and motion corrected reconstructed signal.
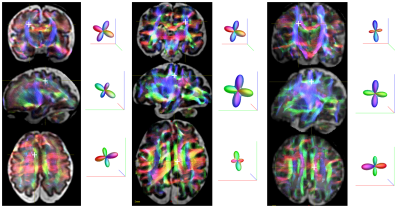
To perform visual evaluation of the reconstructed data we performed constrained spherical deconvolution9 of the reconstructed diffusion signal and whole brain probabilistic tractography using MRtrix5. Figure 3 shows several examples of anatomically plausible fiber crossings in each of the three fetal subjects.
Conclusion
In this abstract we proposed a comprehensive framework for reconstruction of fetal dMRI using higher-order SH representation that supports anatomically plausible reconstruction of fiber crossings in the developing fetal brain. Our method can support application of standard diffusion analysis in a fetal population, opening opportunities for in depth investigation of connectivity and microstructure in the developing fetal brain.Acknowledgements
This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
This work received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/20072013)/ERC grant agreement no. 319456 (dHCP project), and was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
References
1. Jiang, S.Z., et al., Diffusion Tensor Imaging (DTI) of the Brain in Moving Subjects: Application to In-Utero Fetal and Ex-Utero Studies. Magnetic Resonance in Medicine, 2009. 62(3): p. 645-65.
2. Oubel, E., et al., Reconstruction of scattered data in fetal diffusion MRI. Medical Image Analysis, 2012. 16(1): p. 28-37.
3. Fogtmann, M., et al., A Unified Approach to Diffusion Direction Sensitive Slice Registration and 3-D DTI Reconstruction From Moving Fetal Brain Anatomy. IEEE Transactions on Medical Imaging, 2014. 33(2): p. 272-289
4. Kuklisova-Murgasova, M. et al., Reconstruction of fetal diffusion MRI using a spherical harmonic model. International Society for Magnetic Resonance in Medicine, 25th Annual Meeting, ISMRM 2017.
5. Tournier, J.D., et al., MRtrix: Diffusion tractography in crossing fiber regions. International Journal of Imaging Systems and Technology, 2012. 22(1): p. 53-66.
6. Kuklisova-Murgasova, M., et al., Reconstruction of fetal brain MRI with intensity matching and complete outlier removal. Medical Image Analysis, 2012. 16(8): p. 1550-1564.
7. Ferrazzi, G. et al., Resting state fMRI in the moving fetus: A robust framework for motion, bias field and spin history correction. NeuroImage 2014,101:555-68.
8. Kuklisova-Murgasova, M., Distortion correction in fetal EPI using non-rigid registration with a Laplacian constraint. IEEE Transactions on Medical Imaging, 2017.
9. Tournier, J.D. et al., Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. Neuroimage, 2007. 35(4): p. 1459-1472.
Figures