1207

Motion-robust sub-millimeter isotropic diffusion imaging through Motion Corrected Generalized Slice Dithered Enhanced Resolution (MC-gSlider) acquisition
Fuyixue Wang1,2, Berkin Bilgic1, Zijing Dong3, Mary Katherine Manhard1, Ned Ohringer1, Bo Zhao1, Melissa Haskell1,4, Stephen F. Cauley1, Qiuyun Fan1, Thomas Witzel1, Elfar Adalsteinsson2,5, Lawrence L. Wald1,2, and Kawin Setsompop1,2

1A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 2Harvard-MIT Health Sciences and Technology, MIT, Cambridge, MA, United States, 3Center for Biomedical Imaging Research, Department of Biomedical Engineering, Tsinghua University, Beijing, China, 4Graduate Program in Biophysics, Harvard University, Cambridge, MA, United States, 5Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA, United States

Synopsis

gSlider is an SNR-efficient acquisition technique for high-resolution diffusion imaging (dMRI). However, subject motion is inevitable during long scans in high-resolution dMRI, leading to potential for artifacts and blurring. In this study, Motion Corrected gSlider (MC-gSlider) is proposed to obtain high-quality dMRI in the presence of large in-plane and through-plane motion, without use of a navigator. A motion-aware reconstruction with spatially-adaptive regularization is developed to achieve good reconstruction, even under difficult through-plane motions. MC-gSlider was demonstrated in-vivo to provide motion-robust, sub-millimeter isotropic dMRI with a motion correction rate of 2s, allowing for good reconstruction in the presence of large motions.

Introduction

High-resolution dMRI is SNR limited, but the recently developed gSlider-SMS technique[1] has now enabled high-quality in-vivo whole-brain dMRI at 600-800um isotropic resolution. However, subject movement is inevitable, leading to potential image degradation and resolution loss. In this study, we extend the gSlider-SMS framework to create a motion-robust dMRI technique termed MC-gSlider that accounts for both in-plane and through-plane subject movements. MC-gSlider achieves accurate reconstruction by correcting for actual bulk motion, in addition to the corrupted phase from physiologic/bulk motion during diffusion-encoding that many approaches target. A navigator-free motion estimation procedure is developed to achieve accurate high-temporal motion estimates every ~2s. Double-basis acquisition and spatially-adaptive regularization reconstruction are employed to enable high quality dMRI even in the presence of large through-plane motion.

Methods

gSlider-SMS: gSlider is a slab-encoding method, similar to Hardamard encoding, but with slice-phase dithering encoding bases designed to provide high SNR per slab-volume for self-navigated phase correction[1]. With 5×gSlider, five RF-encoding volumes are acquired sequentially and combined to resolve slab to slices. 5×gSlider can also be combined with SMS at 2×MB, to obtain an SNR-efficient 10 slices/shot imaging.

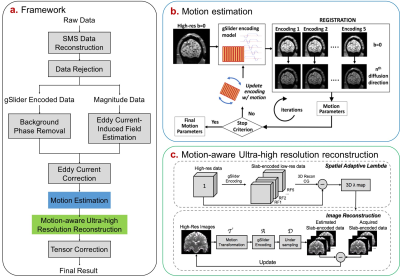
MC-gSlider: Framework of MC-gSlider is illustrated in Fig.1a.

Motion estimation: The gSlider slab-encoding creates contrast modulations that cause a direct time-series motion registration across slab-encoded volumes with different RF-encodings to fail. Therefore, motion parameters for each RF-encoded volume are estimated relative to a corresponding b=0s/mm2 volume of the same RF-encoding (Fig.1b). Nonetheless, sub-voxel subject movements along the slice-encoding direction could still induce contrast differences between diffusion-weighted volume and b0 volume of the same RF encoding, leading to registration errors. Therefore, the proposed estimation method iteratively updates motion parameters by registering the diffusion-weighted volume to a newly encoded b0 volume of the same RF-encoding, updated by current motion estimates. With slice-interleaved acquisition, such motion estimation can be performed every TR/2(~2s).

Motion-aware reconstruction: Motion estimates are incorporated into the following gSlider model for motion-aware reconstruction:

$$x=argmin_{x}\parallel DATx-y \parallel _2^2 +\lambda \parallel x \parallel _2^2$$

where y is the slab-encoded data after correction of background phase and eddy-current; x is the high-resolution volume to be reconstructed; T is the estimated motion transformation matrix[2]; A is the gSlider encoding matrix, D is the sampling matrix.

To address the ill-posed problem caused by through-plane motions, two repetitions of a full RF-encoded gSlider data are acquired consecutively (double-basis) for each diffusion direction to provide more encoding information in the presence of motion. To account for spatially-varying motion in the reconstruction and to avoid over-regularizing well-conditioned regions in the imaging volume, spatially-varied regularization is employed by using a 3D λ map created as shown in Fig.1c, for each motion-corrupted volume.

Experiments: Three experiments were performed to assess MC-gSlider:

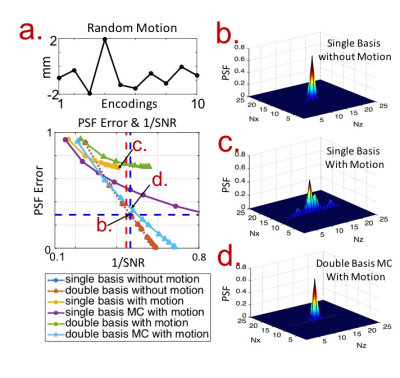
i) Theoretical trade-offs of gSlider and MC-gSlider were evaluated in terms of SNR vs. image point-spread-function (PSF, i.e. effective resolution), where the effect of through-plane motion and estimation errors were also incorporated.

ii) Phantom simulations were performed using 860um gSlider data, with added in-plane and through-plane motion and noise to validate the proposed method.

iii) Motion-corrupted in-vivo gSlider: 860um data with 44-direction at b=1000s/mm2 were acquired on a subject who was instructed to move throughout the 33-minutes scan, where up to 4 mm/degrees motions were detected. All data were acquired on MGH-UCLA 3T Connectom scanner with custom-built 64-channel coil using 2×MB and 5×gSlider, with double-basis. Motion registration and eddy-current estimation were performed using FSL[3-6].

Results

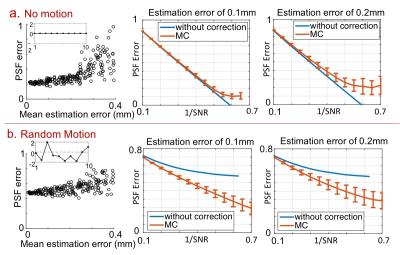
i) In the present of large through-plane motion, conventional gSlider cannot achieve good slice-resolution (low PSF error) at any level of SNR trade-off, while the proposed MC reconstruction combined with double-basis can achieve similar PSF-SNR trade-off as in standard acquisition without motion (Fig.2). In the presence of moderate estimation errors, the MC-gSlider still performs similarly to gSlider in no-motion case, and performs much better when motion is present (Fig.3).

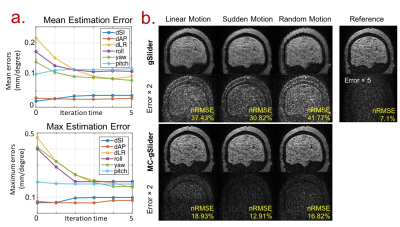
ii) Motion estimation errors of the proposed approach decreases to half that of conventional registration method (0th-iteration) after 3 iterations, and the reconstructed images by MC-gSlider have much lower errors and artifacts (Fig.4).

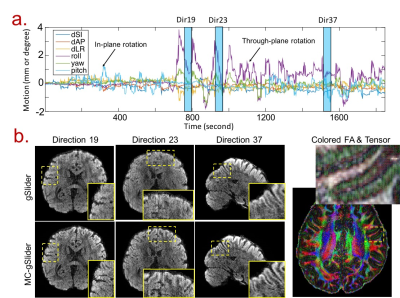
iii) MC-gSlider significantly reduced motion-related blurring in diffusion images and recovered detailed structures around the cortex (Fig.5).

Discussion and Conclusion

The comprehensive motion correction in MC-gSlider is possible through gSlider RF-encoding in the slice direction, which allows high-SNR images to be reconstructed directly from each slab-encoded acquisition. In addition to enabling high-temporal, navigation-free motion estimation, this feature also uncouples the motion correction problem from parallel imaging reconstruction, making motion correction much more tractable. MC-gSlider was employed to achieve, for the first time, motion-robust sub-millimeter isotropic dMRI with accurate fine-scale brain structures in presence of large movements.

Acknowledgements

This work was supported in part by NIH research grants: R01EB020613, R01EB019437, R24MH106096, P41EB015896, and the shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043.

References

1. Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T. High‐resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gSlider‐SMS). Magn. Reson. Med. 2017.

2. Cordero-Grande L, Teixeira RPA, Hughes EJ, Hutter J, Price AN, Hajnal JV. Sensitivity encoding for aligned multishot magnetic resonance reconstruction. IEEE Trans. Comput Imaging, 2016;2:266-280.

3. Andersson JLR and Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 2016;125:1063-1078.

4. Jenkinson M and Smith SM. A global optimisation method for robust affine registration of brain images. Med. Image Anal., 5:143-156, 2001.

5. Jenkinson M, Bannister PR, Brady JM, and Smith SM. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 2002;17:825-841.

6. Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in FSL. NeuroImage, 2009;45:S173-S186.

Figures

Figure 1. (a) The framework of the proposed motion-robust technique based on gSlider-SMS including data preprocessing, (b) iterative motion estimation and (c) motion-aware reconstruction. In the motion estimation, the newly encoded b0 image is obtained by passing a high-resolution b0 volume (created from a b0 gSlider acquisition at the beginning of the scan, assumed motion-free) through a gSlider-encoding simulation that incorporates motion information obtained from each iteration.

Figure 2. Comparison of reconstruction performance for single-basis and double-basis acquisitions, with and without motion correction. Fig2a. shows PSF error vs. 1/SNR curves controlled via regularization parameter, with theoretical SNR gain of √5 for 5xgSlider shown as red vertical dotted-line. The operating point at the cross of the blue dotted-lines represents reconstruction with an SNR level of √4.6 and PSF side-lobe level of 8%. Note that SNRs of double-basis data were divided by √2 to compensate for the doubled acquisition time. PSFs together with PSF errors for b,c,d points marked by arrows in Fig2a. are shown on the right.

Figure 3. Effects of motion estimation error on MC-gSlider reconstruction of double-basis data, without motion (a) and with random motion (b). The scatter plots on the left, each consists of 200-points of simulated motion cases, are PSF errors as a function of mean estimation error (where regularization parameter in the reconstruction was chosen so that the reconstruction’s SNR was hold constant at √4.6). Shown on the right are the PSF error distributions (mean and standard deviation bars) across different reconstruction’s SNR levels, for two mean estimation errors of 0.1mm and 0.2mm, for gSlider reconstruction without correction and for MC-gSlider reconstruction.

Figure 4. (a) Motion estimation’s mean and maximum errors as a function of iteration times. (b) Comparison of the conventional gSlider and MC-gSlider for reconstruction of data with linear motion, sudden motion, and random motion (±2mm motion range for all six rigid motion parameters). The reconstructed images along with their corresponding error maps (×2) and nRMSEs are shown. The error map (×5) below is the reference corresponds to the reconstructed case without any motion, indicating the level of simulated Gaussian noise.

Figure 5. (a) Estimated subject motions as a function of time. (b) Selected reconstructed images from large motion periods, using conventional gSlider and MC-gSlider reconstructions. Imaging parameters were: FOV=200×134×181mm3; 860um isotropic resolution, Rinplane×Rzoom=2×1.64; gSlider×MB=5×2; double-basis encoding; partial Fourier=6/8; TE/TReffective=68ms/42s (TR/volume =4.2s); effective echo spacing=0.317ms, 44 diffusion-directions at b=1000s/mm2 and 3 b=0 images. Zoom-ins of the images are also shown on the bottom right of each image. Colored-FA and zoomed-in tensor results obtained by the MC-gSlider are shown on the bottom right.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1207