1206
Can we correct for interactions between subject motion and gradient-nonlinearity in diffusion MRI?1CUBRIC, Cardiff University, Cardiff, United Kingdom, 2Royal United Hospitals Bath, NHS Foundation Trust, Bath, United Kingdom
Synopsis
Scanners with ultra-strong gradients promise unprecedented opportunities for diffusion imaging. However, their effective use requires correction of gradient-nonlinearity effects during data analysis. Although such techniques exist, they neglect the effects of motion which induces spatio-temporal variations in b-values and b-vectors. Here, we propose a technique that accounts for interaction of subject motion with such non-linearity and study its effectiveness by performing diffusion experiments with volunteers positioned in regions with incrementally increasing gradient-nonlinearities. Our experiments reveal the importance of accounting for motion-induced spatio-temporal variations in B-matrices and our proposed technique corrects most gradient-nonlinearity effects.
Introduction
Recently developed ultra-strong gradients (100, 300 mT/m) are known to have significant gradient-nonlinearities.1,2 This necessitates accurate head positioning and dedicated diffusion data processing pipelines1,3 that account for gradient-nonlinearity-induced spatial variations in B-matrices.4-8
However, gradient-nonlinearity effects become more complicated when a subject moves, as the effect of diffusion-weighting cannot be captured by B-matrix rotations alone.9 To quantify diffusion-weighting effects accurately under such circumstances, spatio-temporal tracking of B-matrices is required. Moreover, the effects of motion also interact with B0-inhomogeneity and eddy-current-induced distortions. Currently there is no tool to disentangle them3 and the optimal order in which to correct for these confounding effects is unclear, with two alternatives being adopted.3,10 In this work we have developed a processing technique that uses spatio-temporally tracked B-matrices for diffusion data analysis and combined it with the two previously proposed pre-processing strategies3,10 and compared the outcomes.
Methods
We performed diffusion experiments on six healthy volunteers on a 300 mT/m Connectom scanner with the following settings- FOV: Transversal 220x220x140 mm3, 2x2x2 mm3 resolution, TR: 2700 ms, TE: 45 ms, GRAPPA and Multiband factor 2, b=1200 s/mm2, 61 spherically distributed b-vectors. Each volunteer underwent diffusion scanning five times, with the brain positioned at the iso-center (best estimate), and -3, -4, -5 and -6 cm away from iso-center (into the scanner bore). Shimming was performed at each translation separately.
Data analysis was performed using six different pipelines, all of which included Spherical-harmonics-based gradient-nonlinearity distortion correction11 (GnD) and either b-vector rotation (BVR) with or without spatial B-matrix correction (SBC), or spatio-temporal B-matrix tracking (STBT):
Pipeline 1: GnD --> FSL topup12, FSL eddy13 --> DTI fit with BVR.
Pipeline 2 (Proposed): GnD --> FSL topup, eddy --> DTI fit with STBT.
Pipeline 3: FSL topup, eddy --> GnD --> DTI fit with BVR.
Pipeline 4 (Proposed): FSL topup, eddy --> GnD --> DTI fit with STBT.
Pipeline 5 (MGH-USC HCP10): Pipeline 1 with BVR and SBC.
Pipeline 6 (WU-Minn HCP3): Pipeline 3 with BVR and SBC.
The proposed pipelines 2 and 4 used the motion parameters estimated by FSL eddy for STBT analysis. For each pipeline, the diffusion parameters obtained from DTI fitting at different bed translations were co-registered to the reference iso-center maps using ANTS(Syn).14 The underlying gradient-nonlinearities were also transformed to the reference space. The resulting co-registered data were used to assess percentage change in DTI parameters as a function of distance from iso-centre, with the hypothesis that pipelines least affected by gradient-nonlinearity and motion would yield near-identical parametric maps irrespective of gradient-nonlinearities.
Results
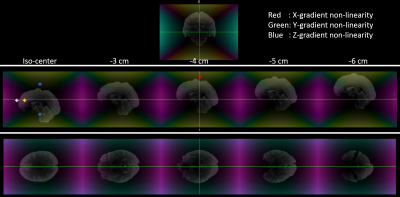
Fig.1 shows the different positions a brain occupies in one dataset at various bed translations, overlaid on the spatially varying gradient amplitudes. Offsets of only 3 cm can give more than 5% deviation in X or Y gradients, highlighting the importance of head positioning.
Gradient-nonlinearity affects diffusivity parameters if unaccounted during parameter estimation. Fig.2 shows MD values estimated from data obtained at various bed translations using different pipelines. Pipelines that ignore gradient-nonlinearities (1 and 3) fail to replicate MD estimates, while pipelines that account for changes in spatial B-matrices (2, 4, 5 and 6) are immune to such discrepancies.
Fig.3 shows the effect of gradient-nonlinearity on FA. We found marked differences in FA values in regions exposed to higher gradient-nonlinearities in 3 out of 5 datasets. We are currently investigating the mechanisms underpinning this behaviour.
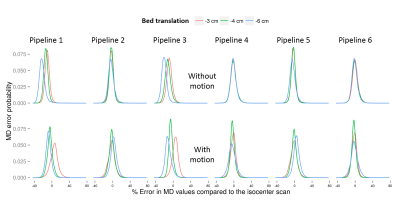
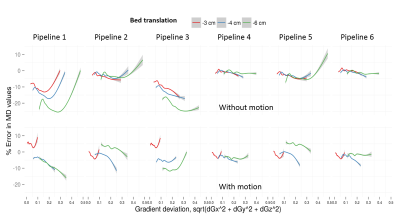
The reliability of different pipelines when the subject moves is revealed through probability density plots of percentage errors in MD values for different bed translations in Fig.4. The improved performance of our proposed pipeline 4 compared to the others is clearly visible. These observations are further supported by plots of parameter errors as a function of underlying gradient deviation as shown in Fig.5. Similar results were observed for AD and RD.
Discussion
Our results confirm the importance of considering gradient-nonlinearity effects while performing diffusion experiments on the Connectom scanner, and also underline the importance of correcting for interactions between motion and gradient-nonlinearities. In particular, the commonly used pipelines 1 or 3 are not suited to analyze Connectom datasets. In the absence of motion, pipelines 4 and 6 outperform pipelines 2 and 5. We attribute this to the assumption of FSL topup that B0-inhomogeneity induces distortions along the phase-encode axis. This can be altered by gradient-nonlinearity distortion correction that occurs earlier in pipelines 2 and 5. In the presence of motion, the superior performance of pipeline 4 is clearly evident and thus should be the preferred choice for all circumstances. This confirms the necessity of spatio-temporal tracking of B-matrices in the presence of motion, which is prevalent in non-compliant participants (e.g., the very young or very old, psychiatric patients) or in longer diffusion scans.Acknowledgements
We would like to acknowledge the help of Dr. Thomas Witzel, MGH, for providing the multi-band diffusion sequence and Dr. Jonathan Polimeni, MGH, for sharing gradient-nonlinearity distortion correction scripts.
The data were acquired at the UK National Facility for In Vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation. The work was supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z).
References
1. Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Essen DCV, Ugurbil K, and Behrens TE. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. NeuroImage, 2013, 80(Supplement C):125 – 143. Mapping the Connectome.
2. Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab J, Keil B, Tisdall M, Hoecht P, Dietz P, Cauley S, Tountcheva V, Matschl V, Lenz V, Heberlein K, Potthast A, Thein H, Horn JV, Toga A, Schmitt F, Lehne D, Rosen B, Wedeen V, and Wald L. Pushing the limits of invivo diffusion MRI for the Human Connectome Project. NeuroImage, 2013, 80(Supplement C):220– 233. Mapping the Connectome.
3. Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Essen DCV, and Jenkinson M. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 2013, 80(Supplement C):105 – 124. Mapping the Connectome.
4. WU-Minn HCP Q1 Release: Reference Manual Appendix II – Matlab code for voxel -wise correction of dMRI gradients.
5. Bammer R, Markl M, Barnett A, Acar B, Alley M, Pelc N, Glover G, and Moseley M. Analysis and generalized correction of the effect of spatial gradient field distortions in diffusion-weighted imaging. Magnetic Resonance in Medicine, 2003, 50(3):560–569.
6. Mohammadi S, Nagy Z, Möller HE, Symms MR, Carmichael DW, Josephs O, and Weiskopf N. The effect of local perturbation fields on human DTI: Characterisation, measurement and correction. NeuroImage, 2012, 60(1):562 – 570.
7. Malyarenko DI, Ross BD, and Chenevert TL. Analysis and correction of gradient nonlinearity bias in apparent diffusion coefficient measurements. Magnetic Resonance in Medicine, 2014, 71(3):1312–1323.
8. Borkowski Karol, K lodowski Krzysztof, Figiel Henryk, and Krzyżak Artur Tadeusz. A theoretical validation of the B-matrix spatial distribution approach to diffusion tensor imaging. Magnetic Resonance Imaging, Nov 2017, 36:1–6. doi: 10.1016/j.mri.2016.10.002.
9. Leemans A and Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. Magnetic Resonance in Medicine, 2009, 61(6):1336–1349.
10. Fan Q, Witzel T, Nummenmaa A, Dijk KRV, Horn JDV, Drews MK, Somerville LH, Sheridan MA, Santillana RM, Snyder J, Hedden T, Shaw EE, Hollinshead MO, Renvall V, Zanzonico R, Keil B, Cauley S, Polimeni JR, Tisdall D, Buckner RL, Wedeen VJ, Wald LL, Toga AW, and Rosen BR. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage, 2016, 124(Part B):1108 – 1114. Sharing the wealth: Brain Imaging Repositories in 2015.
11. Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, MacFall J, Fischl B, and Dale A. Reliability in multi-site structural MRI studies: Effects of gradient non-linearity correction on phantom and human data. NeuroImage, 2006, 30(2):436 –443.
12. Andersson JL, Skare S, and Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage, 2003, 20(2):870 – 888.
13. Andersson JL and Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 2016, 125(Supplement C):1063 – 1078.
14. Avants B, Epstein C, Grossman M, and Gee J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis, 2008, 12(1):26 – 41. Special Issue on The Third International Workshop on Biomedical Image Registration-WBIR 2006.
Figures
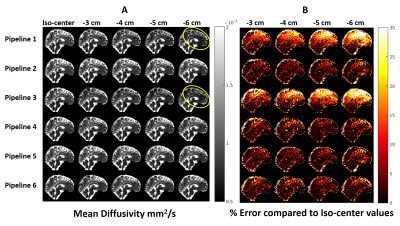
A: Representative MD values in a volunteer estimated using different processing pipelines with data acquired at different bed translations. Pipelines 1 and 3 severely under-estimated MD in the frontal and upper-cortical regions (marked with yellow ellipses), where gradient-nonlinearity effects were most severe. Other pipelines could successfully mitigate gradient-nonlinearity effects.
B: % Error in MD estimates relative to iso-center values. Even at 3 cm offset, pipelines 1 and 3 underestimate MD by up to 30% and progressively worsen as gradient-nonlinearity increases. Other pipelines maintain near-identical performance despite severe gradient-nonlinearities.