1202

A 3D k-Space Fourier Encoding and Reconstruction Framework for Simultaneous Multi-Slab Acquisition
Erpeng Dai1, Yu-hsuan Wu1, and Hua Guo1

1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, China

Synopsis

3D multi-slab acquisition is an important technique for high-resolution isotropic diffusion imaging. To further accelerate the acquisition, simultaneous multi-slice (SMS) excitation can be combined with multi-slab. Although either multi-slab or SMS acquisition can be described using a 3D k-space, it’s hard to describe simultaneous multi-slab (SMSlab) using a 3D k-space. In this study, it’s shown that by using RF modulation and gradient encoding together, SMSlab acquisition can also be described by a 3D k-space. It’s further demonstrated that parallel imaging techniques, such as 2D SENSE and 2D GRAPPA, can be used to recover the under-sampled k-space from SMSlab.

Purpose

3D multi-slab acquisition has been an important technique for high-resolution isotropic diffusion imaging (1-4). To further accelerate the acquisition, simultaneous multi-slice (SMS) excitation can be combined with multi-slab (5-7). Although either multi-slab or SMS acquisition can be described using a 3D Fourier encoding framework, it’s hard to describe simultaneous multi-slab (SMSlab) using a 3D k-space. The underlying reason is that the inter-slab and intra-slab dimensions are represented by the same physical z-gradient axis. When adding gradient encoding in the slice direction, it will contribute to both the inter-slab and intra-slab kz encoding (8). In this study, it’s shown that by using RF modulation (9) and gradient encoding (10) together, SMSlab acquisition can also be described by a 3D k-space. It’s further demonstrated that parallel imaging techniques, such as 2D SENSE (11) and 2D GRAPPA (12), can be used to recover the under-sampled k-space from SMSlab.

Methods

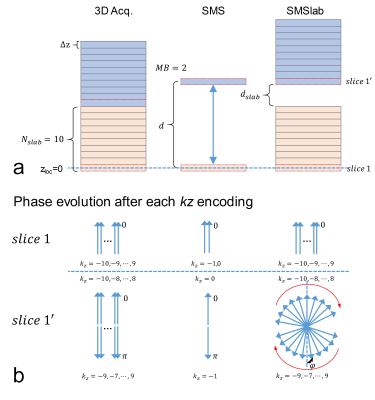
First, the challenge in representing the SMSlab acquisition with a 3D k-space is described. Fig. 1 shows a comparison among 3D acquisition, SMS acquisition and SMSlab acquisition. For simplicity, only the phase evolution of slice 1 and 1’ are plotted (Fig. 1b). In the 3D and SMS acquisitions, as the slices are contiguous, the phases generated by each gradient encoding satisfy the Fourier encoding requirement (Fig. 1b). In the SMSlab acquisition, the phase evolution of slice 1 is still equivalent to 3D acquisition. However, the inter-slab gap will introduce a phase offset kz*φ to slice 1’, which makes slice 1’ violate the Fourier encoding requirement. Thus 3D k-space cannot be directly used.

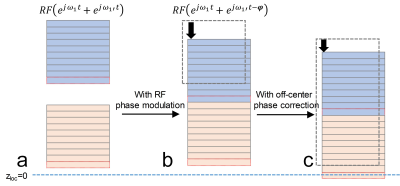
As known, the multiband RF pulse is a sum of MB frequency modulated RF pulses, RFMB=RF(ejω1t+ejω1't). If RF pulse for slab 1’ is further phase modulated with -kz*φ, RFMB=RF(ejω1t+ejω1't-kz*φ) , the inter-slab gap induced phase kz*φ from gradient encoding will be cancelled. Slab 1 and 1’ will be stitched with no gap (Fig. 2b). RFMB is updated for each kz plane. When slice 1 is not at the gradient isocenter, another phase offset ψ will be induced. However, ψ is the same for all slices in SMSlab and can be removed during reconstruction, as in blipped-CAIPI (10). After the RF phase modulation and off-center phase correction, the SMSlab acquisition will be exactly as the 3D acquisition in Fig 1 and can be described using a 3D k-space.

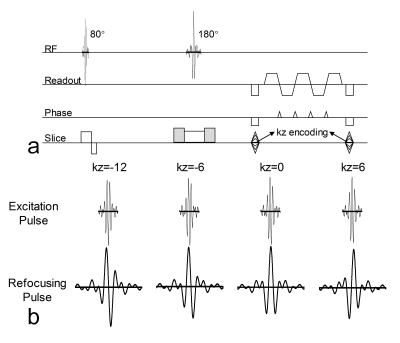
Both phantom and in vivo brain data were acquired on a Philips 3.0T Achieva TX MRI scanner (Philips Healthcare, Best, The Netherlands) using a 32-channel head coil. 10 slabs (MB=2 × 5 slabs) were acquired in total. For each slab, 12 slices (20% oversampling in the kz direction) were acquired, and adjacent slabs were overlapped by 3 slices. Other main imaging parameters were: FOVxy=213×213 mm2, resolution=1.3 mm3, partial Fourier factor=0.7 (ky direction) for image-echo, TE/TR=82 ms/2 s. A 2D EPI sequence is modified for SMSlab acquisition (Fig. 3a). For each kz plane, 4-shot interleaved EPI (iEPI) was used. With careful design, the multiband pulses can be only magnitude modulated (Fig. 3b). Low-resolution (2.6 mm3) 2D single-shot EPI (ssEPI) images were acquired as references.

The data were first fully-sampled and then manually 2-fold under-sampled with CAIPI sampling trajectories, namely 2 out of 4 shots were used for each kz plane. Then 2D GRAPPA was used to recover the missing data.

Results

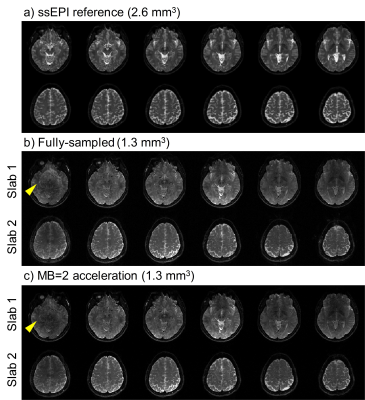
The phantom results are shown in Fig. 4. Both the fully-sampled and MB=2 under-sampled data were well reconstructed, compared with the ssEPI references. Note that the slab boundary aliasing artifacts patterns are different from single slab acquisition. Slices from different slabs are mixed together (yellow arrow heads), rather than intra-slab aliasing. Second, non-uniform signal dropout (red arrow heads) is observed at the slab boundary, which might be due to the B1 inhomogeneity.

The in vivo results (Fig. 5) are consistent with the phantom. Moreover, it’s observed that the inter-slab aliasing artifacts are degraded in the MB=2 results (yellow arrow heads). This might be due to the coil sensitivity constraints in the reconstruction process, which needs further investigation.

Discussion and Conclusion

It’s demonstrated that by RF modulation and gradient encoding, SMSlab acquisition can be described using a 3D Fourier encoding framework. However, as the slab boundary aliasing patterns change in SMSlab, existing boundary artifacts correction methods (2,3) may need further optimization. The feasibility of the proposed method has been demonstrated using non-diffusion encoded SMSlab acquisition. When applying SMSlab to diffusion imaging, physiological motion can cause phase variations among different shots (13,14) and extra phase correction methods should be considered (6,15,16).

Acknowledgements

No acknowledgement found.

References

1. Engstrom M, Skare S. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn Reson Med 2013;70:1507-1514.

2. Van AT, Aksoy M, Holdsworth SJ, Kopeinigg D, Vos SB, Bammer R. Slab profile encoding (PEN) for minimizing slab boundary artifact in three-dimensional diffusion-weighted multislab acquisition. Magn Reson Med 2015;73:605-613.

3. Wu W, Koopmans PJ, Frost R, Miller KL. Reducing slab boundary artifacts in three-dimensional multislab diffusion MRI using nonlinear inversion for slab profile encoding (NPEN). Magn Reson Med 2016;76:1183-1195.

4. Chang HC, Hui ES, Chiu PW, Liu X, Chen NK. Phase correction for three-dimensional (3D) diffusion-weighted interleaved EPI using 3D multiplexed sensitivity encoding and reconstruction (3D-MUSER). Magn Reson Med 2017:n/a-n/a.

5. Frost R, Jezzard P, Porter DA, Tijssen R, Miller K. Simultaneous multi-slab acquisition in 3D multi-slab diffusion-weighted readout-segmented echo-planar imaging. In International Society for Magnetic Resonance in Medicine, 21st Annual Meeting & Exhibition, 22Y26 April, 2013.

6. Bruce IP, Chang HC, Petty C, Chen NK, Song AW. 3D-MB-MUSE: A robust 3D multi-slab, multi-band and multi-shot reconstruction approach for ultrahigh resolution diffusion MRI. Neuroimage 2017;159:46-56.

7. Chang H-C, Hui ES, Liu X, Chiu P-W, Chen N-k. Three-Dimensional Multiplexed Sensitivity Encoding and Reconstruction (3D-MUSER): 3D Phase Correction for 3D Multi-Shot DWI. In Proceedings of the 25th Annual Meeting of ISMRM, Honululu, HI, USA, 2017. Abstract 1094.

8. Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R. RF-Encoding for Simultaneous Multi Slab Imaging. In Proceedings of the 24th Annual Meeting of ISMRM, Singapore, 2016. Abstract 3257. 9. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 2005;53:684-691.

10. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012;67:1210-1224.

11. Weiger M, Pruessmann KP, Boesiger P. 2D SENSE for faster 3D MRI. MAGMA 2002;14:10-19.

12. Blaimer M, Breuer FA, Mueller M, Seiberlich N, Ebel D, Heidemann RM, Griswold MA, Jakob PM. 2D-GRAPPA-operator for faster 3D parallel MRI. Magn Reson Med 2006;56:1359-1364.

13. Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med 1994;32:379-387.

14. Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med 2003;50:343-353.

15. Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 2013;72:41-47.

16. Ma X, Zhang Z, Dai E, Guo H. Improved multi-shot diffusion imaging using GRAPPA with a compact kernel. Neuroimage 2016;138:88-99.

Figures

Fig. 1 (a) Imaging diagram for 3D acquisition, simultaneous multi-slice (SMS) acquisition and simultaneous multi-slab (SMSlab) acquisition. Here, the number of slices in each slab is Nslab=10 and the SMS factor is MB=2. Different color represents different slabs. (b) The phase evolution diagram for two slices (slice 1 and 1’) from different slabs. Each arrow represents the phase induced by the z-gradient at a kz location (kz values are also marked). In SMSlab, the gap between different slabs introduce extra phase kz*φ. For simplicity, it’s assumed that slice 1 is at the gradient isocenter.

Fig. 2 (a) The original slice locations without RF phase modulation. (b) The equivalent slice locations after RF phase modulation. (c) The equivalent slice locations with further off-center phase correction. The dashed box indicates the slice location of last step.

Fig. 3 (a) Sequence diagram for an SMSlab acquisition, modified from a 2D EPI sequence. (b) Four different excitation and refocusing RF pulse sets for different kz planes (kz=-12, -6, 0 and 6) are shown for demonstration. It should be noted the multiband pulses are only magnitude modulated.

Fig. 4 The phantom results: (a) low-resolution ssEPI as references; (b) fully-sampled results; (3) the manually 2-fold under-sampled results using 2D GRAPPA reconstruction. 6 out of 12 slices (slice 1, 3, …, 11) in each slab are provided.

Fig. 5 The in vivo results: (a) low-resolution ssEPI as references; (b) fully-sampled results; (3) the manually 2-fold under-sampled results using 2D GRAPPA reconstruction. 6 out of 12 slices (slice 1, 3, …, 11) in each slab are provided.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1202