Introduction

Magnetic Resonance Fingerprinting (MRF) is a novel transient state relaxometry method that simultaneously estimates multiple quantitative tissue parameters¹. In MRF several time-point images are acquired with varying sequence parameters to produce tissue specific signal evolutions (fingerprints), which can be matched to previously simulated signals (dictionary). MRF has been shown to have some motion resistance¹, however motion can still produce considerable artefacts in the parametric maps^2,3. Misregistration between time-points will cause fingerprint mismatch, leading to incorrect T₁/T₂ estimation. Additionally, if some data sharing method is used (e.g. low rank approximation), motion artefacts (blurring and ghosting) may appear and propagate into the parametric maps. Here we propose to estimate motion from the data itself and use it to correct the k-space followed by a low rank reconstruction (MC-LrMRF) to accelerate the scan. We investigated MC-LrMRF to correct for 2D in-plane motion on standardized T₁/T₂ phantom and in-vivo brain acquisitions. Through-plane motion is a potential source of bias in 2D MRF, since the spin history is corrupted. Thus, we additionally investigated the effect of through-plane motion in 2D MRF in-vivo with the proposed retrospective approach.

Methods

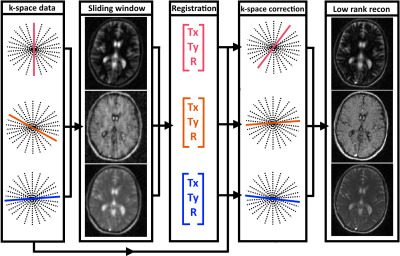
The proposed MC-LrMRF is divided in four steps, as shown in Figure 1. 1) An intermediate sliding window iterative SENSE reconstruction is performed:$$$\bf{\hat{I}_t}=\it{arg min_{\bf{I_t}}}||\bf{EI_t-K_t}||_2^2$$$, where $$$\bf{\hat{I}_t}$$$ are the reconstructed intermediate time-point images, $$$\bf{E}$$$ is the SENSE encoding operator and $$$\bf{K_t}$$$ is the k-space for a sliding window around time t. 2) Motion estimation of $$$\bf{\hat{I}_t}$$$: rigid body image registration is performed to estimate the motion through the intermediate time-point images. 3) k-space motion correction: the acquired k-space $$$\bf{K}$$$ is modified with the corresponding phase shifts and rotations, producing $$$\bf{K^{'}}$$$. 4) Low rank^4,5 (motion corrected) reconstruction: $$$\bf{\hat{I}}=\it{arg min_{\bf{I}}}||\bf{EU_rI-K^{'}}||_2^2$$$, where $$$\bf{\hat{I}}$$$ is the compressed time-point image series and $$$\bf{U_r}$$$ is a temporal compression operator obtained from a truncated (to the appropriate rank r) singular value decomposition of the MRF dictionary.

Experiments

A standardized T1/T2 phantom⁶ and four healthy subjects were scanned in a 1.5T Philips MR scanner using a 12-channel head coil. A protocol similar to⁷ was used with some modifications: fixed TE/TR = 1.2/4.3 ms, 1750 time-points and a golden radial trajectory with a single spoke per time-point. Remaining relevant parameters include: 2x2 mm² resolution, 320x320 mm² FOV, 10 mm slice thickness. For the phantom acquisition, the phantom was continuously moved by hand. For the brain scans, subjects were instructed for three scans: 1) no motion; 2) continuous in-plane motion (yaw); 3) continuous through-plane motion (roll). The sliding window reconstruction featured a window of 50 time-points; image registration was performed with normalized mutual information and the low rank reconstruction used rank r = 15. Both reconstruction steps were solved with the Conjugate Gradient algorithm, limited to 15 iterations.

Results

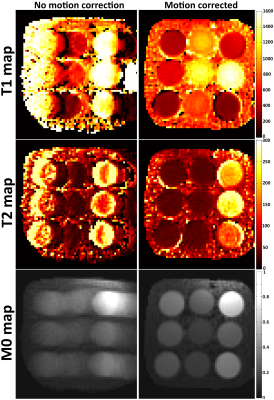
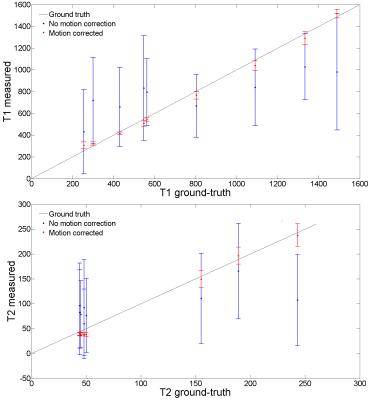
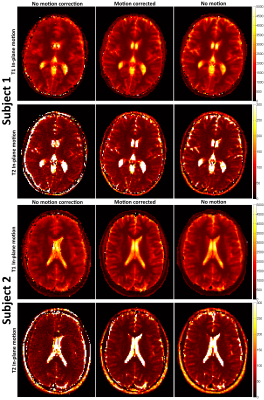
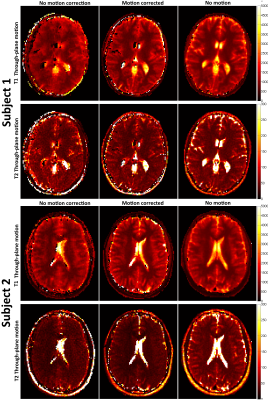
Phantom parametric maps and corresponding T₁/T₂ plots in comparison to gold standard values are shown in Fig.2 and Fig.3, respectively. Considerable blurring artefacts are seen without motion correction, which are successfully removed with the proposed MC-LrMRF method. Plots further demonstrate how motion correction recovers accuracy and precision in the parametric maps. Parametric maps for two representative subjects with in-plane motion are shown in Fig.4. Again, motion artefacts propagate into the parametric maps when motion is not accounted for. The proposed MC-LrMRF successfully corrects for motion during the scan, and leads to parametric maps with similar quality to the case of no motion. Results for the two corresponding subjects with through-plane motion are shown in Fig.5. Although retrospective 2D motion correction helps, considerable artefacts remain in the parametric maps (particularly in T₂), since the corrupted spin history is not accounted for.

Conclusion

A novel method for MRF motion correction was proposed. Motion is estimated from the data itself and used to correct the k-space before a low rank reconstruction. The proposed approach achieves good parametric map quality for in-plane motion, comparable to the case of no motion. Considerable artefacts remain for through-plane motion since the proposed retrospective 2D rigid motion correction does not account for spin history corruption. Future work will consider 3D acquisitions and prospective motion correction solutions to address the limitation of through-plane motion.

Acknowledgements

ACKNOWLEGDMENTS: This work was supported by EPSRC EP/P001009/1 and FONDECYT 1161055.