1171

Robust rigid-body motion estimation from extremely short subsets of 3D Cartesian scans

Gregory R Lee^1,2

¹Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, ²Radiology, University of Cincinnati, School of Medicine, Cincinnati, OH, OH, United States

Synopsis

In this work, the ability to accurately co-register 3D volumes reconstructed from subsets of a variable-density 3D Cartesian acquisition is shown. Accurate rigid-body motion correction was possible for undersampling factors as high as a factor of 125 in a brain imaging application employing a 32-channel head coil. This enables efficient retrospective motion correction without loss of scan efficiency and without the need for any specialized MR hardware. This approach may help reduce the incidence of failed scans due to motion, potentially leading to a reduction for the need for sedation in pediatric patients.

Introduction

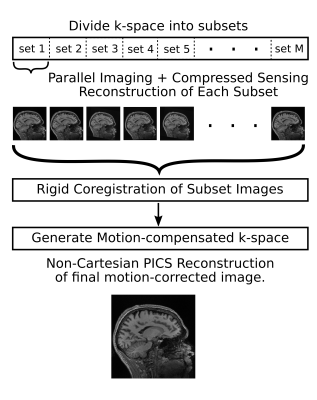
Subject motion is a persistent source of image artifacts in MRI; particularly for relatively long, high resolution 3D acquisitions¹. Motion at any point during the scan can lead to non-diagnostic images. Existing motion correction approaches result in either reduced scan efficiency (separate navigator acquisitions^2,3 or redundant sampling⁴) or require specialized hardware^5,6. Propeller⁴ is an approach that allows 2D motion correction via estimation of motion from repeatedly acquired central k-space data. For rigid motion as encountered for the brain, a rotation of the object corresponds to a matching rotation of it’s k-space and a spatial shift of the object translates into a linear phase in k-space. A 3D data sampling approach that enables true 3D rigid motion correction with almost no redundant sampling has been proposed⁷. In this work, the accuracy of registration as a function of acceleration factor is investigated in detail.

Methods

To demonstrate the accuracy of motion estimation, a fully sampled T1-weighted MP-RAGE dataset was acquired on a 3T Philips Achieva scanner equipped with a 32 channel head coil [FOV=180x240x240 mm, resolution=1.9x0.6x0.6 mm, TR/TE = 9.4/4.6 ms, flip angle = 8 degrees, shot interval 2800 ms, TI 941 ms]. Fourier reconstruction of the fully sampled k-space was performed to provide a ground truth reference volume. The ground-truth k-space was then retrospectively undersampled using a variable density sub-sampling scheme^8,9 for 3D Cartesian MRI (400x400 phase encoding matrix) at a total acceleration of ~5.1 (N=40064 total samples). The sampling pattern is designed to become progressively denser with time and is approximately isotropically distributed for all subsets of length N/2, N/4, N/8, N/16, N/32, N/64 and N/128 of the full set of samples (Fig. 2). The proposed motion-robust 3D acquisition technique⁷ is summarized in Fig. 1. The present work is focused on the accuracy of the motion estimation step as a function of the degree of undersampling used for each temporal subset of data. The k-space dataset was truncated to a single subset equal in length to a given acceleration factor. A series of 16 angular rotations in the sagittal plane were then drawn from a uniform random distribution in the range [-5, 5] degrees. The same data subset was then reconstructed using k-space coordinates rotated by each of these randomly generated angles. Coregistration of the rotated images to the reference was performed using fMRIB’s linear image registration tool (FLIRT¹⁰). All image reconstructions were performed using iterative non-Cartesian parallel imaging and compressed sensing (PICS) based on the fast iterative soft thresholding (FISTA) algorithm¹¹. A Non-Cartesian approach is required due to the rotation of the k-space samples away from their original Cartesian sampling coordinates. The regularization term used was the L₁ norm of discrete wavelet coefficients (with cycle-spinning employed across iterations¹²).

Results

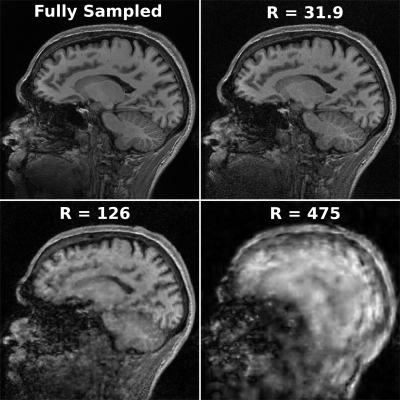
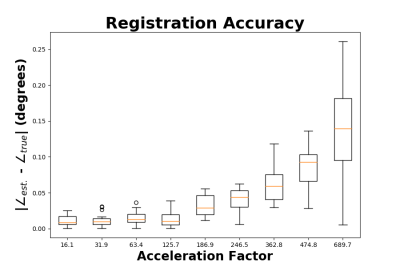
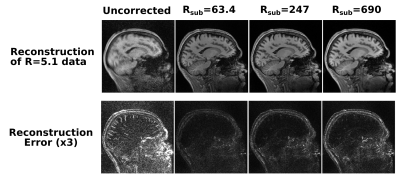
Fig. 3 shows the representative image quality of the 3D PICS reconstruction for a set of subsampling factors as compared to the ground truth image. Fig. 4 demonstrates the magnitude of the error of the angular rotation estimate when co-registering images over a wide range of acceleration factors. Surprisingly, registration accuracy remains high even for extremely high accelerations (well beyond where raw image quality becomes substantially degraded). A progressively larger error in the angular estimates occurs for undersampling factors above a factor of 125. Fig. 5 shows reconstruction of a full dataset without correction of motion (left) and after recombination of subsets of k-space that have been corrected based on the estimated motion parameters. For the two higher acceleration factors a moderate degree of apparent blur due to minor errors in the motion estimate is apparent. All cases result in a huge improvement over the uncorrected case, which produces a non-diagnostic image.

Discussion

One aspect not treated in this work is the presence of within-subset motion. Such subsets could potentially be identified as outliers based on a metric such as the mean squared error between a given frame and the mean motion-corrected subset. These subsets with intra-subset motion could then be dealt with by either discarding them or by dividing them into finer temporal subsets and repeating the motion estimation over these.

Conclusions

Diagnostic quality images were demonstrated based on retrospective correction of motion from subsets of an undersampled, motion-corrupted 3D dataset. Accurate motion estimation was found to be possible for subsets accelerated as much as a factor of 125 (approximately 10 seconds of data per subset). The proposed sampling patterns have almost no redundant samples and enable true 3D motion correction as opposed to corrections only within the slice plane (e.g. PROPELLER).

Acknowledgements

No acknowledgement found.

References

1. Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J Magn Reson Imaging 2015;52(4):887-901.

2. Ehman RL, Felmlee JP. Adaptive technique for high-definition MR imaging of moving structures. Radiology 1989;173(1):255-263.

3. White N, Roddey C, Shankaranarayanan A, Han E, Rettmann D, Santos J, Kuperman J, Dale A. PROMO: Real-Time Prospective Motion Correction in MRI using image-based tracking. Magn. Reson. Med. 2010;63(1):91-105.

4. Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magn Reson Med 1999;42(5):963–969.

5. Ooi MB, Krueger S, Thomas WJ, Swaminathan SV, Brown TR. Prospective real-time correction for arbitrary head motion using active markers. Magn Reson Med. 2009;62(4): 943-954.

6. Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic resonance imaging of freely moving objects; prospective real-time motion-correction using an external optical motion-tracking system. Neuroimage 2006;32(3):1038-1050.

7. Lee G. Motion-robust 3D MRI Without the Use of Navigators or External Tracking Hardware. In: Proceedings of the Organization for Human Brain Mapping, 22nd Annual Meeting, Geneva, Switzerland, 2016; p.1588.

8. Lee GR, Griswold MA. An electrostatic charge repulsion algorithm for dynamic ordering of 3D projections. In: Proceedings 20th Scientific Meeting, International Society for Magnetic Resonance in Medicine 2012; p.2283.

9. Griswold MA, Lee GR. Ordering projections for magnetic resonance. U.S. Patent 9,086,466 B2; 2015.

10. Jenkinson M, Bannister P, Brady M, Smith S. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. NeuroImage 2002;17(2): 825-841.

11. Beck A, and Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2002; 2(1):183–202.

12. Guerquin-Kern M, Van De Ville D, Vonesch C, Baritaux JC, Pruessmann KP. Wavelet-regularized reconstruction for rapid MRI. In: IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2009; 193-196.

Figures

Overview of the motion-compensated 3D reconstruction approach. Image from subsets of the data are produced by a parallel imaging + compressed sensing (PICS) reconstruction. Motion parameters estimated from these M images are used to correct the corresponding segments of k-space. The full set of corrected k-space data is then used to produce the final motion-compensated reconstruction.

Example of variable density k-space subsampling patterns used in this study. Points were generated using an electostatic charge repulsion algorithm and then snapped to the nearest Cartesian grid point to create a sampling mask for 3D Cartesian MRI. Sampling occurs in a progressive fashion, so that the same type of relative sampling density pattern is present for many choices of subset width. Both the acceleration factor, R, and the number of samples, N, corresponding to each pattern are shown.

Example reconstructions of a single k-space subset for various choices of acceleration factor. As expected, use of a higher acceleration results in a reduction in resolution and signal-to-noise ratio. The visual quality of these images is not important, only the relative ability to coregester frames at a given subsampling rate.

Average magnitude of the error in the angular rotation estimate for a set of 16 randomly generated rotations distributed uniformly in the range [-5, 5] degrees. Equivalent for all tested acceleration factors <= 125. Above R=125, further acceleration of the subsets results in a progressive loss of registration accuracy.

The full set of variable density k-space samples (R=5.1) had random angular rotations in the range +/-5 degrees applied to 16 different equal-length subsets of the data. The leftmost column is the result of reconstructing the timeseries without any motion correction. The remaining three columns generate the motion correction proposed in Fig. 1 for subsets of the data corresponding to 3 different acceleration factors (relative to full sampling). The bottom row shows the error relative to fully sampled ground-truth acquisition (multiplied by 3 for visibility).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1171