1160
Predicting the spatio-temporal evolution of tumor vasculature and cellularity following whole brain radiation therapy1Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, United States, 2Department of Diagnostic Medicine, The University of Texas at Austin, Austin, TX, United States, 3Department of Biomedical Engineering, The University of Texas at Austin, Austin, TX, United States, 4Livestrong Cancer Institutes, The University of Texas at Austin, Austin, TX, United States
Synopsis
A fundamental challenge in the care of patients with brain tumors is the limitation of standard radiographic measurements to accurately evaluate, let alone predict, patient response. To address this challenge, we have developed a biophysical model of tumor growth, angiogenesis, and response to radiation therapy that is calibrated on a subject-specific basis using diffusion-weighted and dynamic contrast enhanced MRI data. We evaluated the predictive accuracy of the model in rats with C6 gliomas receiving whole brain radiation. The model accurately predicted future tumor volume (error ranged from 12.1 to 18.5%).
Introduction
A fundamental challenge in the care of patients with brain tumors is the limitation of standard radiographic measurements to accurately evaluate, let alone predict, patient response. To this end we are developing computational approaches that incorporate a subject’s imaging data into mechanistic models of tumor growth and response. In this effort, we evaluate the predictive accuracy of a biophysical description of tumor growth calibrated from diffusion weighted MRI (DW-MRI) and dynamic contrast-enhanced MRI (DCE-MRI) data collected in a murine model of glioma before and after whole brain radiation.Methods
In vivo data: Wistar rats (n=7) with C6 gliomas were imaged with DW-MRI and DCE-MRI at three-time points (t1-t3) before treatment and four-time points (t4-t7) after treatment with each imaging session spaced 48 hours apart. MRI experiments were performed on a 9.4 T magnet over a 32×32×16 mm3 field of view sampled with a 128×128×16 matrix. DW-MRI data was acquired using a pulsed gradient spin echo diffusion sequence with three diffusion encoding directions with b-values of 150, 500, and 1000 s/mm2. DCE-MRI data was collected using a spoiled gradient echo sequence before and then following the injection of Gd-DTPA. A T1 map was also acquired using an inversion-recovery snapshot sequence. Tumor regions of interest (ROIs) were determined from enhancing regions in DCE-MRI data. Cell number was estimated within tumor ROIs using ADC maps estimated from DW-MRI1. The blood volume fraction was estimated within tumor regions from DCE-MRI data. Rats received either a 20 Gy (n=3) or a 40 Gy (n=4) dose of x-ray radiation delivered over whole brain between t3 and t4.
Biophysical Model: The spatiotemporal evolution of tumor cell number and blood volume fraction were described using a system of two, coupled partial differential equations. The tumor cell equation in the absence of radiation consisted of a reaction-diffusion2 type model with a mechanically coupled diffusion term3, a logistic growth proliferation term, and a cell death term as a function of blood volume fraction. In a similar fashion, the blood volume equation consists of a mechanically coupled diffusion term, a logistic growth proliferation term, and a cell death term. The effects of radiation therapy are applied to both the tumor cells and vasculature and is modeled as having an early effect (i.e., instantaneous death) and a long-term effect (i.e., reduced proliferation). The coupled biophysical models were implemented using a finite difference approach with explicit time differentiation.
Model Calibration and Validation: Model parameters describing tumor cell and blood volume diffusion, proliferation, death, and efficacy of radiation therapy were calibrated in 3D on an individual basis from MRI data using a hybrid simulated annealing Levenberg-Marquardt algorithm. Data on t1-t3 were used to calibrate growth parameters in the absence of therapy, while data on t4 were used to calibrate the effect of radiation therapy. The calibrated parameters were then used in a forward evaluation of the model. Error was assessed by calculating the percent error between the predicted and observed tumor volume. The level of agreement between voxel predictions of tumor cell number and blood volume fraction to their measured quantities was assessed using the concordance correlation coefficient (CCC).
Results
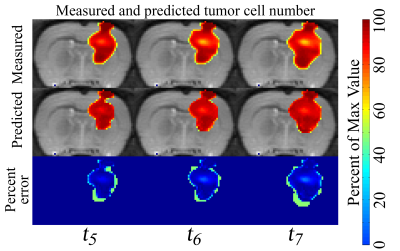
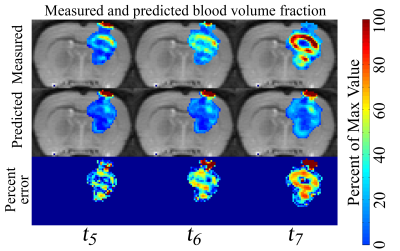
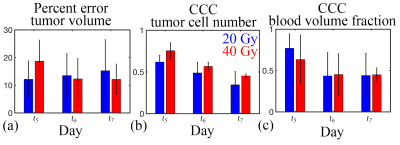
In Figure 1, low error was observed between the measured and predicted volume (ranged from 6% to 13%) and a high level of agreement was observed at the voxel-level (CCCs from 0.55 to 0.67) for a rat receiving 20 Gy. Similarly, in Figure 2, a high level of agreement (CCCs from 0.27 to 0.85) was observed between the predicted and measured blood volume fraction. A similar trend was observed for the cohort, Figure 3, where less than 15.3% error was observed for the rats receiving 20 Gy and less than 18.5% error was observed for the rats receiving 40 Gy. A high level of agreement between the predicted and the observed tumor cell number and blood volume fraction was observed on t5 and t6 (greater than 0.50 and 0.45, respectively).Discussion
The results of this study indicate that these models can be used to accurately predict future tumor volume, while less accurately predicting the intra-tumor distribution of tumor cells. By incorporating vasculature information, were are now able to evolve the net tumor cell proliferation rate as a function of changes in local blood volume fraction and predict the development of areas of necrosis.Conclusion
This experimental and computational study demonstrates the potential predictive capabilities of biophysical models informed from an individual's own imaging data. Future modeling efforts will investigate developing optimized therapy plans based on pre- and post-treatment data.Acknowledgements
We gratefully acknowledge the support of NCI U01 CA174706, U01 CA154605, and CPRIT RR 160005References
1. Atuegwu NC, Arlinghaus LR, et al. Integration of diffusion-weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy. Man Reson Med. 2011;66(6):1689-1696
2. Burger M, Di Francesco M, et al. Nonlinear cross-diffusion with size exclusion. SIAM J Math Anal. 2010;42(6);2842:2871
3. Hormuth II DA, Weis JA, et al. A mechanically-coupled reaction-diffusion model that incorporates intra-humoral heterogeneity to predict in vivo glioma growth. J R Soc interface. 2017;14(128)
Figures