1132

Magnetization Transfer effects in Actual Flip angle Imaging

Shaihan J Malik¹, Rui Pedro A.G. Teixeira¹, and Joseph V Hajnal¹

¹School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom

Synopsis

The AFI sequence is a robust flip angle mapping method and is used within quantitative MRI protocols. AFI is a modified spoiled gradient echo (SPGR) sequence, employing interleaved TR times of different lengths. It is well known that SPGR signal behaviour is sensitive to Magnetization Transfer effects, so in this work we used a two-pool model to derive signal equations for AFI that include MT. We found that MT will lead to an underestimation of flip angle by up to 6% in white matter and that longer TR and lower RF energy lead to larger bias.

Introduction

B₁⁺ field mapping is required for characterizing inhomogeneity seen at high field (B₀≥3T). Accuracy is particularly important when using B₁⁺ maps for quantitative MRI, since small errors in B₁⁺ estimation may translate non-linearly to the parameter value estimates^1,2. The actual flip-angle³ (AFI) sequence is a modified spoiled gradient echo (SPGR) acquisition with interleaved TR times (TR₁ and TR₂=nTR₁). AFI has been shown to be robust when using strong gradient spoiling^4,5,6, and has been used for a variety of quantitative techniques^4,7–10. However it has also been well demonstrated that SPGR sequences are sensitive to magnetization transfer (MT) effects, and that these will lead to a bias when used for quantitative purposes¹¹. Hence we investigated potential MT effects on the AFI sequence.

Theory

MT effects can be well described using a “two-pool” model in which longitudinal magnetization has two components $$$\mathbf{M_z}=[M_z^f M_z^r]^T$$$ where $$$M_z^f$$$ is ‘free’ (observable) magnetization and $$$M_z^r$$$ is ‘restricted’ magnetization associated with macromolecules and not directly observed. During evolution periods the modified Bloch equations¹² are written $$$\mathbf{\dot{M}_z}=\mathbf{\Lambda M_z +C}$$$ where:

$$\mathbf{\Lambda} = \begin{bmatrix} -R_1^f-k & k/f \\ k & -R_1^r -k/F\end{bmatrix}$$

and

$$\mathbf{C}=\begin{bmatrix} R_1^f M_0^f \\ R_1^r M_0^r \end{bmatrix}$$

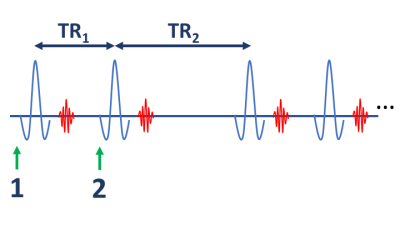
Each pool has its own relaxation rate $$$R_1^{f,r} $$$; k is the exchange rate from free to restricted pool; and F is the ratio of pool sizes $$$\frac{M_0^r}{M_0^f}$$$. An RF pulse of flip angle $$$\alpha$$$ rotates the free-pool and saturates the bound-pool, so $$$\mathbf{M_z \rightarrow \Theta M_z}$$$. Here $$$\mathbf{\Theta}=\begin{bmatrix} \cos\alpha & 0\\ 0 & e^{-\pi\gamma^2 G E_{rf}}\end{bmatrix}$$$ where G is the absorption rate of the tissue¹³ and $$$E_{rf}$$$ is RF pulse energy in units $$$\mu T^2 ms$$$. Figure 1 shows a sequence diagram. Steady-state expressions for magnetization at points 1 and 2 (i.e. directly before each RF pulse) are:

$$\mathbf{ M_z^1 = \left(1 - \Xi_2\Theta\Xi_1\Theta\right)^{-1}\left(\Xi_2\Theta\left(\Xi_1-1\right)+\left(\Xi_2-1\right)\right)\Lambda^{-1}C }$$

$$\mathbf{ M_z^2 = \Xi_1\Theta M_z^1 + \left(\Xi_1-1\right)\Lambda^{-1}C }$$

where $$$\mathbf{\Xi_{1,2}} = \exp\left(\mathbf{\Lambda}TR_{1,2}\right)$$$.

Methods

Apparent flip angle $$$\hat{\alpha}$$$ was estimated using the standard AFI formula³ on the ratio $$$\frac{M_z^{f,2}}{M_z^{f,1}}$$$ . MT parameters for white matter (k=4.3s^-1,F=0.132;T₁=779ms) and gray matter (k=1.8s^-1,F=0.062,T₁=1211ms) were taken from Gloor et al¹⁴. Following Gloor et.al, we fix $$$R_1^f=R_1^r$$$ and $$$T_2^r=12\mu s$$$. A single healthy adult volunteer was imaged at 3T using AFI with $$$\alpha=60°$$$, $$$E_{rf}=48.7\mu T^2ms$$$, resolution 1.5x1.5x3mm³, 30mm slab size for TR₁=30,50,60 and 80ms with n=5. Strong gradient spoiling was employed.

Results

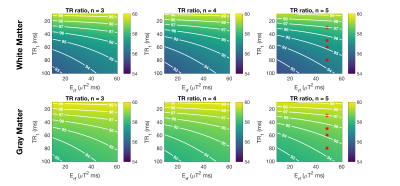
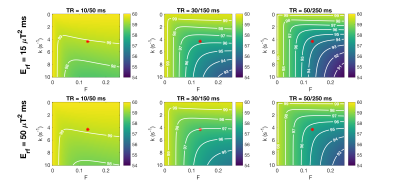
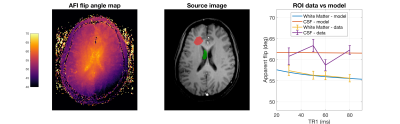
Figure 2 shows variation in $$$\hat{\alpha}$$$ for actual flip angle 60° as TR₁ and $$$E_{rf}$$$ are varied for sequences with n=3,4,5 in both white matter (WM) and gray matter (GM). $$$\hat{\alpha}$$$ falls as TR₁ increases, and as $$$E_{rf}$$$ is reduced. Figure 3 shows how $$$\hat{\alpha}$$$ would vary for a tissue with the same T₁ as white matter, but as k and F vary; $$$\hat{\alpha}$$$ falls as k or F increases (setting either to zero represents a tissue with no MT). As Figure 2 also showed, the effects are much more marked for the lower $$$E_{rf}$$$ and longer TR₁ sequences. Figure 4 shows the in-vivo result, including a flip angle map (TR₁=80ms, n=5). ROI measurements are plotted against predicted $$$\hat{\alpha}$$$ for white matter, and CSF as a control (no MT). The model predictions were adjusted to account for the fact that B₁⁺ is lower in the WM ROI than CSF because of the existing B₁⁺ ‘doming’ effect (CSF+3%,WM-2%). The WM data appears to follow the downward trend as TR₁ increases, predicted by the model. The ventricles stand out with a higher flip angle than surrounding tissue; this is consistent with flip angle being systematically underestimated in surrounding WM.

Discussion & Conclusion

Predictions suggest that the AFI sequence will systematically underestimate the flip angle in WM, worsening as TR₁ increases or $$$E_{rf}$$$ falls. A small reduction in $$$\hat{\alpha}$$$ would be expected as TR₁ increases, simply because the assumption that TR<<T₁ is increasingly violated. However this is a smaller effect (see k=0 on Fig.3) – the MT effects enhance this significantly. Further, it is counterintuitive that the effect should worsen as TR₁ increases and $$$E_{rf}$$$ falls, since MT effects are classically associated with high RF power. A possible explanation is that lower $$$E_{rf}$$$ leaves the restricted pool less saturated, so more prominent in the dynamics of the system. The brightness of the ventricles in AFI has been observed by others, and even postulated as a real electromagnetic effect¹⁵. The two-pool model suggests MT as another possible explanation, however Brink et.al observed the effect using many B₁⁺ mapping sequences, which would be unlikely to all have similar MT sensitivity. Experimental data obtained so far suggests some agreement with the model, however more precise measurements are needed. If confirmed, although a small effect, MT influence on AFI could be a confound for qMRI/qMT methods that use it for making predictions with complex models.

Acknowledgements

This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1, EPSRC fellowship award (EP/L00531X/1) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

1. Lankford, C. L. & Does, M. D. Propagation of error from parameter constraints in quantitative MRI: Example application of multiple spin echo T2 mapping. Magn. Reson. Med. 0, (2017).

2. Helms, G., Dathe, H. & Dechent, P. Quantitative FLASH MRI at 3T using a rational approximation of the Ernst equation. Magn. Reson. Med. 59, 667–672 (2008).

3. Yarnykh, V. L. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 57, 192–200 (2007).

4. Yarnykh, V. L. Optimal radiofrequency and gradient spoiling for improved accuracy of T1 and B1 measurements using fast steady-state techniques. Magn. Reson. Med. 63, 1610–26 (2010).

5. Nehrke, K. On the steady-state properties of actual flip angle imaging (AFI). Magn. Reson. Med. 61, 84–92 (2009).

6. Lutti, A. et al. Robust and fast whole brain mapping of the RF transmit field B1 at 7T. PLoS One 7, 1–7 (2012).

7. Voigt, T., Katscher, U. & Doessel, O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn. Reson. Med. 66, 456–66 (2011).

8. Teixeira, R. P. A. G., Malik, S. J. & Hajnal, J. V. Joint System Relaxometry (JSR) and Cramer-Rao Lower Bound Optimization of Sequence Parameters: A Framework for Enhanced Precision of DESPOT T1 and T2 Estimation. Magn. Reson. Med. 0, (2017).

9. Katscher, U. et al. Determination of electric conductivity and local SAR via B1 mapping. IEEE Trans. Med. Imaging 28, 1365–74 (2009).

10. Hurley, S. A. et al. Simultaneous variable flip angle - Actual flip angle imaging method for improved accuracy and precision of three-dimensional T 1 and B 1 measurements. Magn. Reson. Med. 68, 54–64 (2012).

11. Ou, X. & Gochberg, D. F. MT effects and T1 quantification in single-slice spoiled gradient echo imaging. Magn. Reson. Med. 59, 835–845 (2008).

12. Sled, J. G. & Pike, G. B. Quantitative Imaging of Magnetization Transfer Exchange and Relaxation Properties In Vivo Using MRI. 931, 923–931 (2001).

13. Graham, S. J. & Henkelman, R. M. Understanding pulsed magnetization transfer. J. Magn. Reson. Imaging 7, 903–912 (1997).

14. Gloor, M., Scheffler, K. & Bieri, O. Quantitative magnetization transfer imaging using balanced SSFP. Magn. Reson. Med. 60, 691–700 (2008).

15. Brink, W. M., Börnert, P., Nehrke, K. & Webb, A. G. Ventricular B1+ perturbation at 7T – real effect or measurement artifact ? 5–8 (2014). doi:10.1002/nbm.3112

Figures

Figure 1: AFI sequence diagram. Labels 1 and 2 correspond to the time points for which steady-state M_z is derived.

Apparent flip angle ($$$\hat{\alpha}$$$) for white and gray matter for a range of TR and E_rf, and a range of n=3,4,5. $$$\hat{\alpha}$$$ decreases with larger TR₁ and smaller E_rf, particularly in white matter, which has stronger MT effects (larger k and F). The effect of n (TR ratio) is weak. The red asterisks correspond to settings that were tested experimentally (Figure 4). Contour labels show $$$\hat{\alpha}$$$ as a percentage of the true flip angle (60°).

Apparent flip angle ($$$\hat{\alpha}$$$) for a range of MT parameters k and F, for a tissue with the same T₁ as white matter. Increasing either the exchange rate (k) or restricted pool size (F) leads to a stronger MT effect and hence a stronger attenuation of ($$$\hat{\alpha}$$$). The effect is much more pronounced for the longer TR sequences, and for lower energy pulses as shown in Fig.2. Red asterisk marks the measured values of k and F for WM¹⁴. Contour labels show ($$$\hat{\alpha}$$$) as a percentage of the true flip angle (60°).

Left: AFI map for TR=80,400. The B₁⁺ doming effect expected at 3T is observed. The ventricles appear more prominent than surrounding tissue. Subtle WM/GM contrast is visible in the flip angle map. Middle: One of the AFI source images with ROIs marked – red=WM, green=CSF. Right: Flip angles measured in ROIs for all acquisitions. Apparent flip angle reduces as TR₁ increases broadly in line with model (nominal flip in each ROI was adjusted to match observations). CSF data is noisy because the underlying signal is low (see image), however there isn’t an overall downward trend in $$$\hat{\alpha}$$$ for this data.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1132