1128
Design of universal parallel-transmit refocusing kT-point pulses and application to 3D T2-weighted imaging at 7T1DRF/Joliot/Neurospin, CEA, Gif sur Yvette, France, 2Siemens Healthcare, Saint Denis, France, 3German Center for Neurodegenerative Diseases (DZNE), Bonn, Germany
Synopsis
The kT-point technique exploits the dynamic RF shimming capability of parallel transmission to uniformly excite the spins. That technique allows homogenizing the flip angle in RF-spoiled sequences but also the rotation angle in sequences involving non-selective refocusing pulses. As far as the flip angle is concerned, it has been shown that so-called universal kT-point pulses can be designed to work robustly on any subject without having to tailor the pulse to the subject. In this study we propose to extend the universality concept to refocusing pulses, and to give an experimental demonstration with 3D fast spin echo brain imaging.
Introduction
The kT-point technique1 exploits the dynamic RF shimming capability of parallel transmission (pTx) to uniformly excite the spins. Successful demonstration of that technique has been shown for brain imaging at 7T with (magnetization prepared) 3D gradient echo sequences,1,2 and more recently with 3D fast spin echo sequences like SPACE3-5. In ref. 5, temporal symmetry was enforced to ensure, near pure resonance, good refocusing properties for large rotation angle (RA). That result is appealing in that kT-points were used for the first time to create refocusing RF pulses. Independently of this, the concept of universal pulse (UP) has been proposed to enable calibration-free pTx6. That new approach indeed makes unnecessary the transmit RF field calibration routine and online RF pulse tailoring but so far has been limited to non-refocusing pulses. In this study we thus propose to extend the UP concept to that new class of pulses, and to implement it for the SPACE sequence.Methods
The SPACE refocusing pulse train (RPT) was built, as proposed in ref. 4, from a unique scalable kT-point pulse (RF coefficients $$$\mathbf{b} \in \mathbb{C}^{N_c\times N_{k_T}}$$$ and kT locations $$$\mathbf{k} \in \mathbb{R}^{3\times N_{k_T}}$$$, $$$N_c$$$ and $$$N_{k_T}$$$ representing the number of transmit channels and kT points respectively). The design of that pulse yet was performed “offline” in two steps using a database of field maps acquired on ten adults of a previous study7.
1) An optimized symmetric parameterization $$$(\mathbf{k}_{\text{sym}},\mathbf{b}_{\text{sym}})$$$ was first obtained by solving numerically under temporal symmetry constraints the usual spatial domain magnitude least-squares problem7 $$$\min_{\mathbf{k},\mathbf{b}} C_{\text{STA}}(\mathbf{k},\mathbf{b})$$$, where $$$C_{\text{STA}}(\mathbf{k},\mathbf{b})$$$ is the root-mean-squares (RMS) distance between the maximum RA of the RPT (the target) and the actual flip angle profile calculated with the small tip angle (STA) approximation.
2) to better mitigate the effect of the static field heterogeneity which tends to degrade the performance of symmetric solutions especially at high flip angles, that solution was used as the initialization point of a second optimization which consisted in minimizing the scaling error (SE):
$$\text{SE}(\mathbf{k},\mathbf{b}) = \text{RMS} \left(\left|\mathbf{U}(\mathbf{k},\mathbf{b})\mathbf{U}_{\text{STA}}^{-1}(\mathbf{k},\mathbf{b})\right|_{\text{f}} - \textbf{Id} \right)$$
where $$$|\cdot|_{\text{f}}$$$ denotes the Fröbenius norm and $$$\mathbf{U},\mathbf{U}_{\text{STA}} \in \mathbb{C}^{2\times 2}$$$ denote the Bloch-simulated RF pulse SU(2) rotation matrix and the STA approximation thereof. Importantly, for this optimization, the time-symmetry constraint was disabled and replaced by the constraint: $$$C_{\text{STA}}(\mathbf{k},\mathbf{b})\le C_{\text{STA}}(\mathbf{k}_{\text{sym}},\mathbf{b}_{\text{sym}})$$$. This second optimization step aimed at preserving the correct rotation matrix when the reference pulse is scaled, in order to faithfully implement the nominal RA train and maintain the CPMG condition. The optimization problems were solved using the Active-Set algorithm under explicit hardware (peak and average power) and SAR constraints8.
Using Average Hamiltonian Theory9, it is possible to express the rotation $$$\mathbf{U}$$$ as $$$e^{-i(\mathbf{A}^{(0)}+\mathbf{A}^{(1)}+\cdots)}$$$. Interestingly, the expression for $$$\mathbf{A}^{(0)}$$$ is in perfect analogy with the STA while $$$\mathbf{A}^{(1)}$$$ appears to vanish at pure resonance when the RF pulse is symmetric. At off-resonance (as is the case when static field is not homogeneous), $$$\mathbf{A}^{(1)}$$$ does not vanish and is found to scale with the energy of the RF pulse. That AHT analysis thus explains why in off-resonant voxels $$$\mathbf{U}$$$ can deviate more rapidly from its STA approximation as the RF amplitude is scaled up.
Measurements were performed on five healthy adults on a 7T scanner equipped with the Nova 8TX-32RX head coil. All scans were run under local SAR supervision mode. A T2-weighted SPACE sequence was first run in circularly-polarized (CP) mode with 1-ms square pulses, then with the scaling-optimized kT-point pulse obtained from the above optimization (9 kT-points, total kT-point pulse duration 1.1 ms). Sequence parameters were: TR 3 s, ES 8.6 ms, BW 290Hz/pixel, ETL 117, 0.8×0.8×0.8 mm3 voxels, Flip Angle (FA) and nominal signal evolution displayed in Figure 1 and TA 7:47min.
Results
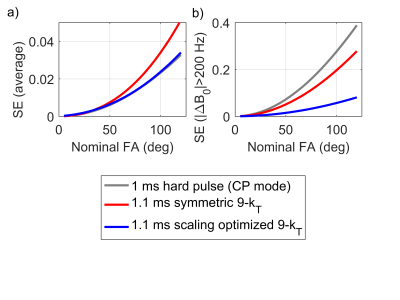
In Fig. 2a, the SE of the square pulse as well as of the symmetric and scaling-optimized solutions are displayed as functions of the nominal RA. As expected, when isolating highly off-resonant voxels, the SE remains small for the scaling optimized solution (Fig. 2b).
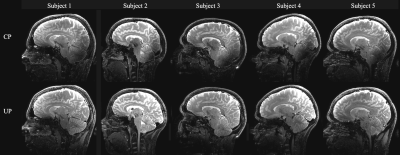
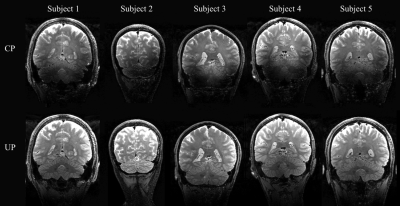
In the SPACE images (Fig. 3 and 4), the CP mode exhibits severe signal dropouts in the temporal lobes and the cerebellum. The use of UPs allows excellent signal recovery to make the UHF SPACE sequence“truly” whole brain.
Conclusion
We have reported an RF pulse design framework for 3D refocusing pulses based on the kT-point approach, extending the field of application of UPs. The experimental results suggest that excellent mitigation of the RF field inhomogeneity problem in 3D fast spin echo sequences can be achieved with UPs, while skipping entirely the pTx calibration and online pulse tailoring workflow.Acknowledgements
The authors thank Dr. E. Pracht and M. Boland (DZNE, Bonn, Germany) for their contribution to the data acquisition. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2016-2017), ERC Proof Of Concept Grant Agreement n. 700812.References
1. Cloos MA, Boulant N, Luong M, Ferrand G, Giacomini E, Le Bihan D, Amadon A. kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magn Reson Med 2012;67:72–80.
2. Cloos MA, Boulant N, Luong M, Ferrand G, Giacomini E, Hang M-F, Wiggins CJ, Bihan DL, Amadon A. Parallel-transmission-enabled magnetization-prepared rapid gradient-echo T1-weighted imaging of the human brain at 7T. NeuroImage 2012;62:2140–2150.
3. Mugler JP. Optimized three-dimensional fast-spin-echo MRI. J. Magn. Reson. Imaging 2014;39:745–767.
4. Massire A, Vignaud A, Robert B, Le Bihan D, Boulant N, Amadon A. Parallel-transmission-enabled three-dimensional T2-weighted imaging of the human brain at 7 Tesla. MRM 2015;73:2195–2203.
5. Eggenschwiler F, O’Brien KR, Gruetter R, Marques JP. Improving T2-weighted imaging at high field through the use of kT-points. Magnetic Resonance in Medicine 2014;71:1478–1488.
6. Gras V, Vignaud A, Amadon A, Le Bihan D, Boulant N. Universal pulses: A new concept for calibration-free parallel transmission. Magnetic Resonance in Medicine 2017;77:635–643. doi: 10.1002/mrm.26148.
7. Gras V, Boland M, Vignaud A, Ferrand G, Amadon A, Mauconduit F, Bihan DL, Stöcker T, Boulant N. Homogeneous non-selective and slice-selective parallel-transmit excitations at 7 Tesla with universal pulses: A validation study on two commercial RF coils. PLOS ONE 2017;12:e0183562.
8. Grissom W, Yip C, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med 2006;56:620–629.
9. Warren WS. Effects of arbitrary laser or NMR pulse shapes on population inversion and coherence. The Journal of Chemical Physics 1984;81:5437–5448. doi: http://dx.doi.org/10.1063/1.447644.
Figures
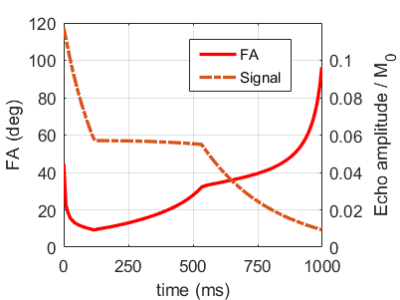
Figure 1. Rotation angle evolution of the refocusing pulse train used for the SPACE (solid red) protocol and generated for T1 = 1400 ms, T2 = 40 ms. The overlaid dashed curve display the respective nominal signal evolutions during the application of the refocusing pulse train, after a 90° excitation with π/2 phase offset.