1095

Mean lung alveolar dimension mapping with hyperpolarized 3He and 129Xe diffusion-weighted MRI

Ho-Fung Chan¹, Guilhem J. Collier¹, and Jim M. Wild¹

¹Academic Unit of Radiology, University of Sheffield, Sheffield, United Kingdom

Synopsis

Lung morphometry parameters can be derived from multiple b-value hyperpolarized gas diffusion-weighted (DW)-MRI using the cylinder (CM) and stretched exponential (SEM) models. Mean alveolar diameter (L_Alv) and diffusive length scale (Lm_D) are calculated from the CM and SEM, respectively. This work compares the parameters L_Alv and Lm_D derived from a range of subjects with both ³He and ¹²⁹Xe DW-MRI. Excellent linear agreement is observed between the L_Alv and Lm_D parameters for both gases. This indicates these parameters are equivalently representative indices of mean alveolar diameter dimension within the range of experimental conditions considered.

Introduction

Theoretical models of gas diffusion have been proposed to derive lung morphometry parameters from the hyperpolarized gas diffusion-weighted (DW)-MRI signal. The cylinder model (CM) is based upon infinitely long non-connected cylinders, and has been used to obtain estimates of acinar airway radius (R) and mean chord length (Lm) from a model of anisotropic diffusion. ^1,2 The stretched exponential model (SEM) is a mathematical model of the non-Gaussian diffusion signal that derives estimates alveolar dimensions (Lm_D) within each voxel from a probability distribution of diffusion length scales. ^3,4

Previously, in vivo comparisons of Lm and Lm_D have demonstrated that the two lung morphometry parameters are related but not identical. ^5,6 The mean alveolar diameter (L_Alv) is an alternative CM parameter that is defined as the chord length of one alveolus in the CM cylindrical airway geometry. ² This work evaluates and compares SEM-derived Lm_D and CM-derived L_Alv from a range of subjects using ³He and ¹²⁹Xe DW-MRI.

Methods

3D multiple b-value DW-MRI datasets were acquired on a 1.5 T GE HDx scanner in 51 and 31 subjects with ³He and ¹²⁹Xe, respectively. ³He and ¹²⁹Xe DW-MRI (³He Δ=1.6 ms, b=[0, 1.6, 4.2, 7.2 s/cm²]; ¹²⁹Xe Δ=8.5 ms, b=[0, 12, 20, 30 s/cm²]) were acquired using compressed sensing as described previously. ^4,7 Healthy volunteers, ex-smokers, idiopathic pulmonary fibrosis (IPF), and COPD patients were recruited, representing a range of acinar microstructural length scales. The ³He and ¹²⁹Xe diffusion signal decay within each voxel was fitted to both the CM and SEM to derive maps of R ² and Lm_D ³, respectively. ¹²⁹Xe DW-MRI was acquired with Δ=8.5 ms; therefore, ³He CM expressions ² were applied to both ³He and ¹²⁹Xe DW-MRI to derive maps of R, ⁷ and L_Alv was subsequently calculated from L_Alv=2Rsin(π/8).

Results and Discussion

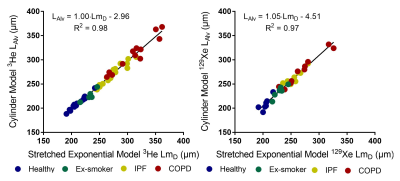
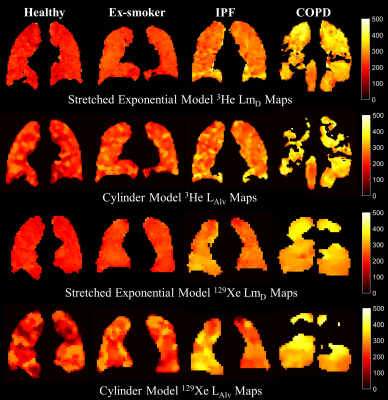
A summary of global ³He and ¹²⁹Xe lung morphometry metrics is provided in Table 1. All metrics for each patient group were larger than those for healthy subjects reflecting the respective changes to acinar microstructure related to fibrosis in the IPF patients, and emphysema for the ex-smokers and COPD patients. A statistically significant linear correlation (P<0.001) between Lm_D and L_Alv was observed for both ³He and ¹²⁹Xe DW-MRI (Figure 1). The linear regression fit (³He β₁=1.00, ¹²⁹Xe β₁=1.05) suggests excellent agreement between the two parameters for both gases, and Bland-Altman analysis confirmed this with small mean bias of +1.0% and -2.6% towards Lm_D for ³He and ¹²⁹Xe, respectively. In the representative L_Alv maps from ³He and ¹²⁹Xe measurements in the same patients (Figure 2), regions of elevated values appear to qualitatively match those observed in corresponding Lm_D maps. The analogous linear correlation and lung morphometry maps demonstrates the same microstructural information can be obtained with both ³He and ¹²⁹Xe.

In a previous comparison, ³He Lm_D was related to Lm by a non-linear power relationship; ⁶ however, the results in this comparison suggests that L_Alv is more comparable to Lm_D than Lm. The two distinct relationships observed between Lm_D with Lm and L_Alv can be associated with the different sections of the acinar airway geometry that is measured by each parameter.

In the CM geometry, eight alveoli units surround the acinar airway such that the chord length of an alveolus matches typical alveolar diameter measurements from histology. ² While in the SEM, Lm_D represents the average distance that ³He or ¹²⁹Xe gas atoms diffuse within the acinar airspace. The maximum Lm_D is constrained by the theoretical free diffusion length of the respective DW-MRI experiments (~500 µm). According to histology, the mean alveolar diameter in healthy adult lungs is approximately 200-250 µm. ⁸ Therefore, in these experiments, gas atoms are predominantly restricted by the alveolar geometry and as such Lm_D, like L_Alv, is reflective of mean alveolar diameter dimensions.

In contrast, the CM-derived Lm is calculated through an inferred relationship between the volume (alveolus and alveolar duct) and surface area of a single alveolus unit. Therefore, the inclusion of the alveolar duct volume in the calculation might allows Lm values that are beyond the theoretical free diffusion lengths of the diffusion experiments, and probably accounts for the mismatch in Lm_D and Lm observed previously. ^5,6

Conclusion

This is the first comparison of mean alveolar diameter parameters derived from the CM and SEM with 3D multiple b-value ³He and ¹²⁹Xe DW-MRI acquired in a range of subjects with a range of severity of microstructural lung changes. L_Alv and Lm_D demonstrated excellent agreement with both gases indicating that these parameters derived from different theoretical gas diffusion models are equivalent.

Acknowledgements

This work was supported by NIHR grant NIHR-RP-R3-12-027 and MRC grant MR/M008894/1. The views expressed in this publication are those of the author(s) and not necessarily those of the NHS, the National Institute for Health Research or the Department of Health.

References

1. Yablonskiy, D. A., et al. (2002). Proc Natl Acad Sci USA 99(5): 3111-3116.

2. Yablonskiy, D. A., et al. (2009). J Appl Physiol (1985) 107(4): 1258-1265.

3. Parra-Robles, J., et al. (2014). Proc ISMRM:3529

4. Chan, H.-F., et al. (2017). Magn Reson Med 77(5): 1916-1925.

5. Ouriadov, A., et al. (2017) Magn Reson Med. doi:10.1002/mrm.26642.

6. Chan, H.-F., et al. (2017). Proc ISMRM:876

7. Chan, H.-F., et al. (2017). Magn Reson Med. doi:10.1002/mrm.26960.

8. Weibel, E. R. (1963). Morphometry of the human lung, Springer-Verlag.

Figures

Table 1: Summary of global ³He and ¹²⁹Xe DW-MRI lung morphometry metrics derived from the cylinder model and stretched exponential model.

Figure 1: Excellent linear agreement is observed between stretched exponential model derived mean diffusive length scale (Lm_D) and cylinder model derived mean alveolar diameter (L_Alv) for both ³He and ¹²⁹Xe in all subjects.

Figure 2: Representative ³He and ¹²⁹Xe maps of SEM-derived Lm_D and CM-derived L_Alv for each patient group. Maps of Lm_D and L_Alv are similar and also comparable with both hyperpolarized gases.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1095