1091
Variational Adversarial Networks for Accelerated MR Image Reconstruction1Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria, 2Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, 3Safety & Security Department, AIT Austrian Institute of Technology GmbH, Vienna, Austria
Synopsis
Inspired by variational networks and adversarial training, we introduce variational adversarial networks for accelerated MR image reconstruction to overcome typical limitations of using simple image quality measures as loss functions for training. While simple loss functions, such as mean-squared-error and structural similarity index, result in low resolution and blurry images, we show that the proposed variational adversarial network leads to sharper images and preserves fine details for clinical low and high SNR patient data.
Introduction
Recent developments in deep learning$$$^1$$$ greatly improve image reconstruction quality over hand-crafted models by learning a suitable model from data$$$^{2-8}$$$. Learning-based approaches do not only rely on the network architecture but also on the loss functions used during training. Typical loss functions are quantitative image quality measures such as the root-mean-squared-error (RMSE) or Structural Similarity Index (SSIM)$$$^9$$$. However, the reconstructed images trained with these measures can appear oversmoothed$$$^{10}$$$ due to the averaging nature of these approaches and their sensitivity to noise. This effect is particularly prominent if the training data is noisy. Generative adversarial networks (GANs)$$$^{11-18}$$$ have been proposed to learn a loss function from data, however, GANs are difficult to train. Inspired by variational networks$$$^{2}$$$ and GANs$$$^{12}$$$, we propose variational adversarial networks to improve sharpness and preserve fine details in image reconstruction of undersampled data from multiple coils.
Methods
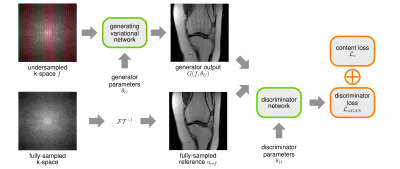
In our proposed adversarial training, two components, i.e., a generator $$$G$$$ and a discriminator $$$D$$$, try to compete with each other: The generator $$$G$$$ generates images from undersampled k-space data $$$f$$$, whereas, the discriminator $$$D$$$ tries to distinguish the generated images from fully-sampled reference images $$$u_{ref}$$$ (see Figure 1). By using the dual Wasserstein distance$$$^{12}$$$, the adversarial training can be cast in the saddle-point formulation:$$\mathcal{L}_{wGAN}=\min\limits_{\theta_G}\max\limits_{\theta_D}\frac{1}{S}\sum\limits_{s=1}^S\left\langle\mathbf{1},D(G(f_s,\theta_G),\theta_D)-D(u_{ref,s},\theta_D)\right\rangle$$where $$$\theta_G,\theta_D$$$ are the parameters of the generator and discriminator, respectively, $$$S$$$ is the number of samples and $$$\mathbf{1}$$$ is a vector of ones with the same dimension as $$$u_{ref}$$$. To guide the generator towards plausible solutions, we additionally stabilize $$$\mathcal{L}_{wGAN}$$$ with a content loss on $$$\epsilon$$$-smoothed magnitude images$$$^2$$$ in conjunction with a diagonal matrix $$$M$$$ that masks out background pixels:$$\mathcal{L}_{c}=\frac{1}{2S}\sum\limits_{s=1}^S\Vert{M}^{\frac{1}{2}}\left(\vert{G}(\theta_G,f_s)\vert_{\epsilon}-\vert{u}_{ref,s}\vert_{\epsilon}\right)\Vert^2_2.$$Considering the mask operator $$$M$$$ and magnitude images in $$$\mathcal{L}_{wGAN}$$$, the full loss reads as:$$\min\limits_{\theta_G}\max\limits_{\theta_D}\frac{1}{S}\sum\limits_{s=1}^S\left\langle\mathbf{1},M\left(D(\vert{G}(f_s,\theta_G)\vert_{\epsilon},\theta_D)-D(\vert{u}_{ref,s}\vert_{\epsilon},\theta_D)\right)\right\rangle+\alpha\mathcal{L}_{c}$$where $$$\alpha$$$ balances the trade-off between $$$\mathcal{L}_{wGAN}$$$ and $$$\mathcal{L}_{c}$$$. For the generator network, we use the variational network architecture$$$^2$$$ with $$$T=10$$$ steps and 24 filter kernels of size $$$11\times 11$$$, trained with $$$\mathcal{L}_{c}$$$ only. For the discriminator, we introduce a network that consists of $$$L$$$ trainable convolution layers $$$K$$$ and activation layers $$$\Psi$$$, depicted in Figure 2:$$D(x)=\Psi_L\left(K_L\Psi_{L-1}\left(K_{L-1}\dots\Psi_1\left(K_1x\right)\right)\right),$$ where $$$x$$$ is the input image to the discriminator. As in the generating variational network, the activation functions are constructed using a weighted combination of radial basis functions$$$^{2,19}$$$. To bound the discriminator, we constrain both the convolution and activation layers according to Figure 2. The discriminator network consists of 4 layers, where layers 1-3 use 16 filter kernels of size $$$3\times 3$$$ and the last layer a single $$$1\times 1$$$ filter kernel. For training the generator and discriminator, we use an alternating projected ADAM optimization scheme with an additional prediction step$$$^{20,21}$$$ in the generator parameters, learning rate $$$2e{-4},\,\beta_1=0.5,\,\beta_2=0.999$$$, 30000 iterations and mini-batch size 5. The content loss weight $$$\alpha=1e{-1}$$$ is estimated empirically for high SNR data and $$$\alpha=7.5e{-2}$$$ for low SNR data. We acquired fully-sampled datasets for two sequences, differing in SNR, of 20 patients undergoing clinical knee exams (IRB approved) using a 3T Siemens Skyra and a 15-channel knee coil. Training was performed slice-by-slice using 200 slices selected from 10 different patients for the individual sequences, which were retrospectively downsampled for an acceleration factor of four. Testing was performed on the remaining 10 datasets not included during training. Coil-sensitivity maps were estimated using ESPIRiT$$$^{22}$$$ from a block of $$$24\times 24$$$ auto-calibration-points at the center of k-space.
Results
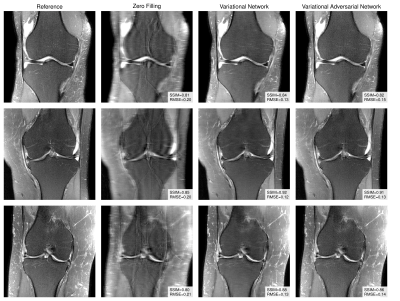
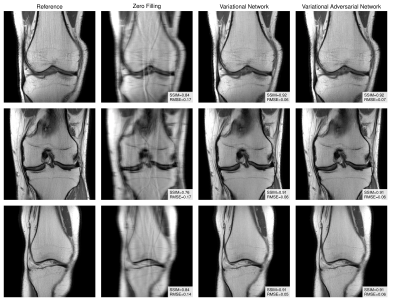
Figure 3 illustrates that the proposed variational adversarial networks preserve fine details much better than the variational network for low SNR images. Although quantitative RMSE and SSIM results for the variational network are superior, the images appear blurry, indicating that these measures are a poor representation of the perceptual system at this level of SNR. For high SNR images (Figure 4), the variational networks perform already well and the variational adversarial networks have similar reconstruction quality, which is confirmed by RMSE and SSIM values.
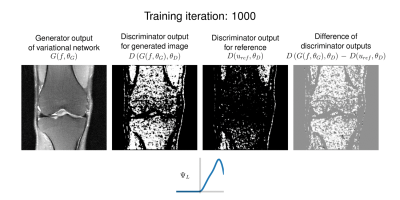
To gain an insight on the function of the discriminator, we plot the discriminator outputs over training iterations in Figure 5. The generator outputs contain successively less artifacts and get sharper, also supported by the difference image. The discriminator outputs indicate which regions are activated and thus are considered to improve the generator.
Discussion
We propose variational adversarial networks to simultaneously learn the reconstructions of accelerated MRI data and the loss function. Using the adversarial learning strategy, we observe improved image quality in terms of sharpness and visibility of fine details compared to variational networks, especially for low SNR data. Once the training of the variational adversarial networks is finished, the generator parameters are fixed and new unseen k-space data can be reconstructed efficiently. Future work will investigate if and how the learned discriminator can be used as quantitative image quality measure.Acknowledgements
We acknowledge grant support from the Austrian Science Fund (FWF) under the START project BIVISION, No. Y729, ERC starting grant ”HOMOVIS”, No. 640156., NIH P41 EB017183, NIH R01 EB000447 and NVIDIA corporation.References
[1] Y. LeCun, Y. Bengio, and G. Hinton, “Deep Learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015.
[2] K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock and F. Knoll. “Learning a Variational Network for Reconstruction of Accelerated MRI Data”. Magnetic Resonance in Medicine (in Press, 2017).
[3] S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, and D. Liang, “Accelerating Magnetic Resonance Imaging Via Deep Learning,” in IEEE International Symposium on Biomedical Imaging (ISBI), pp. 514–517, 2016.
[4] K. Kwon, D. Kim, H. Seo, J. Cho, B. Kim, and H. W. Park, “Learning-based Reconstruction using Artificial Neural Network for Higher Acceleration,” in Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 1081, 2016.
[5] E. Gong, G. Zaharchuk, and J. Pauly, “Improving the PI+CS Reconstruction for Highly Undersampled Multi-Contrast MRI Using Local Deep Network,” in Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 5663, 2017.
[6] J. Schlemper, J. Caballero, J. Hajnal, A. Price, and D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction,” in Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 643, 2017.
[7] B. Zhu, J. Liu, B. Rosen, and M. Rosen, “Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation,” in Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 640, 2017.
[8] D. Lee, J. Yoo, J. C. Ye. “Compressed Sensing and Parallel MRI using Deep Residual Learning”, In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 641, 2017.
[9] Z. Wang, A. C. Bovik, H. R. Sheikh, E. P. Simoncelli, “Image quality assessment: from error visibility to structural similarity”, IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600-612, 2004.
[10] H. Zhao, O. Gallo, I. Frosio, and J. Kautz, “Loss Functions for Image Restoration With Neural Networks”, IEEE Transactions on Computational Imaging, vol. 3, no. 1, pp. 47-57, 2017.
[11] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. “Generative Adversarial Nets”. Advances in Neural Information Processing Systems 27, pp. 2672-2680, 2014.
[12] M. Arjovsky, S. Chintala, L. Bottou, “Wasserstein GAN”, arXiv:1701.07875, 2017.
[13] P. Isola, J.-Y. Zhu, T. Zhou, A. A. Efros, “Image-to-Image Translation with Conditional Adversarial Networks”, arXiv:1611.07004, 2016.
[14] C. Ledig, L. Theis, F. Huszar, J. Caballero, A. Aitken, A. Tejani, J. Totz, Z. Wang, W. Shi. “Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network”. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 4681-4690, 2017.
[15] O. Shitrit, T. R. Raviv. “Accelerated Magnetic Resonance Imaging by Adversarial Neural Network”. In Proceedings of Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: Third International Workshop, pp. 30-38, 2017.
[16] M. Mardani, E. Gong, J. Y. Cheng, S. Vasanawala, G. Zaharchuk, M. Alley, N. Thakur, S. Han, W. Dally, J. M. Pauly, L. Xing. “Deep Generative Adversarial Networks for Compressed Sensing (GANCS) Automates MR”, arXiv:1706.00051, 2017.
[17] T. M. Quan, T. Nguyen-Duc, W. Jeong, “Compressed Sensing MRI Reconstruction with Cyclic Loss in Generative Adversarial Networks”, arXiv:1709.00753, 2017.
[18] Q. Yang, P. Yan, Y. Zhang, H. Yu, Y. Shi, X. Mou, M. K. Kalra, G. Wang, “Low Dose CT Image Denoising Using a Generative Adversarial Network with Wasserstein Distance and Perceptual Loss”, arXiv:1708.00961, 2017.
[19] Y. Chen, W. Yu, T. Pock. “On Learning Optimized Reaction Diffusion Processesfor Effective Image Restoration.” In Proceedings of the IEEE Conference onComputer Vision and Pattern Recognition (CVPR), pp. 5261-5269, 2015.
[20] A. Chambolle, T. Pock. “A first-order primal-dual algorithm for convex problemswith applications to imaging”, Journal of Mathematical Imaging and Vision, vol. 40, no. 1, pp. 120-145, 2011.[21] A. Yadav, S. Shah, Z. Xu, D. Jacobs, T. Goldstein, “Stabilizing Adversarial Nets With Prediction Methods”, arXiv:1705.07364, 2017.
[21] A. Yadav, S. Shah, Z. Xu, D. Jacobs, T. Goldstein, “Stabilizing Adversarial Nets With Prediction Methods”, arXiv:1705.07364, 2017.
[22] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala and M. Lustig. “ESPIRiT - An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE meets GRAPPA”. Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990-1001, 2014.
Figures