1076

Usage of Octahedral Shear Strain Weights in the Inversion of Multifrequency MR Elastography

Cemre Ariyurek^1,2, Bilal Tasdelen^1,2, Eric Barnhill³, Arif Sanli Ergun⁴, Yusuf Ziya Ider¹, and Ergin Atalar^1,2

¹Department of Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, ²National Magnetic Resonance Research Center (UMRAM), Ankara, Turkey, ³Radiological Sciences, Charité - Universitätsmedizin Berlin, Berlin, Germany, ⁴Department of Electrical and Electronics Engineering, TOBB-University of Economics and Technology, Ankara, Turkey

Synopsis

Multifrequency MR elastography (MMRE) is useful for compensating the influence of amplitude nulls on the elastogram by combining computations at different frequencies by amplitude-weighted averaging or directly without using weights. Previously, it was shown that strain‑SNR measures the quality of the data for reconstructing accurate elastography maps. Therefore, using octahedral shear strain (OSS) weights may lead to more accurate elastograms. In this study, k-MDEV and multifrequency Helmholtz inversion have been used. Including OSS-weights in the inversions yielded more reliable elastograms for simulation and experiment phantom. Furthermore, elastograms in higher resolution were obtained for the brain model and human brain data.

Introduction

Inversion techniques involving multifrequency MR elastography (MMRE) compensate the influence of amplitude nulls on the elastograms^1,2, by combining computations at different frequencies by amplitude‑weighted averaging or directly without any weighting. Because shear strain relates to shear modulus, strain‑SNR is more reliable than motion-SNR to estimate data quality in reconstructing elastography maps³. Therefore, combining inversions at different frequencies using octahedral shear strain (OSS) weighted averaging or using OSS weights prior to the inversion, may give more reliable maps⁴. The purpose of this study is to investigate the effect of OSS-weighting on multifrequency inversion techniques such as k-MDEV² and multifrequency Helmholtz inversion¹.

Methods

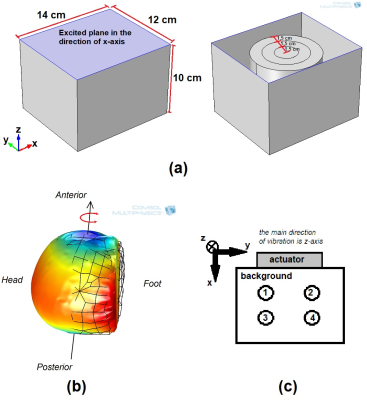
To conduct MR elastography (MRE) simulations, frequency domain analysis was performed on a 3D phantom model developed in COMSOL Multiphysics (COMSOL, Stockholm, Sweden) finite element method (FEM) software by assigning prescribed displacement to the excitation plane, as depicted in Figure 1a. Furthermore, a 3D brain model consisting of scalp, skull, falx cerebri, cerebrospinal fluid, gray matter and white matter, developed from segmented brain images of a healthy human^5,6, was imported to COMSOL Multiphysics. Both for the phantom and brain model, Young’s modulus, Poisson’s ratio, density and damping parameters were assigned, regarding the values reported in previous studies^7,8,9,10. Frequency domain analysis was performed by rotationally vibrating the head about y-axis, as shown in Figure 1b. MRE experimental data, MMRE phantom, reported in previous studies^1,2 (Fig. 1c), and human brain data acquired in a recent study¹¹, were used. The brain data were obtained with 2 mm isotropic voxels and excitation frequency was swept from 20 to 60 Hz with 5 Hz increments. For multifrequency inversion of the simulation and experiment phantom, k-MDEV² was implemented, which uses amplitude-weighted averaging to combine computations at different frequencies. As an additional multifrequency inversion technique, we used OSS‑weighted averaging instead of amplitude-weighted averaging, where other steps of inversion were same with k-MDEV. Using k-MDEV on brain data does not yield good results possibly due to brain sulci. Therefore, for the elasticity inversion of the simulation and human brain data, multifrequency Helmholtz inversion¹ was used and results for conventional inversion (no-weighting) and OSS-weighted were compared. Note that OSS weights were added using weighted-least-squares method prior to the inversion.

Results

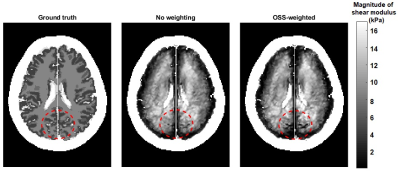
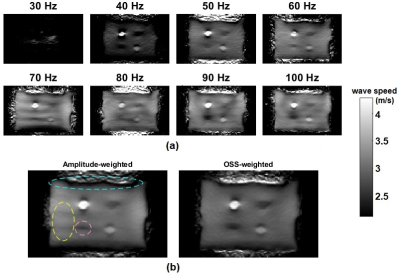
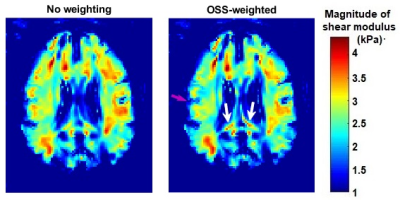
Elasticity inversion results are compared in Figure 2 for the simulation phantom and in Figure 3 for the brain model. For the experiment phantom, individual wave speed maps reconstructed at different frequencies are depicted in Figure 4a and combined wave speed maps by amplitude-weighted averaging and OSS‑weighted averaging are shown in Figure 4b. Finally, inversion results obtained from human brain experiments are demonstrated in Figure 5.

Discussion

For the simulation phantom data, using OSS-weighted instead of amplitude-weighted averaging in k-MDEV inversion yielded a more accurate wave speed map, where wave speed values and geometry of the phantom were estimated inaccurately in amplitude‑weighted averaging (Fig. 2). From the inversion results of phantom experiment data, depicted in Figure 4b, it can be seen that the lower left inclusion is more visible and the background has less wave artifacts in OSS-weighted averaging compared to amplitude-weighted averaging. Notice that, wave artifacts are present in the wave speed map at 70 Hz, as seen in Figure 4a, which are also observed in amplitude-weighted averaging inversion result but successfully suppressed in OSS-weighted averaging inversion result. In addition, OSS-weighted averaging gives better results on the boundaries (Fig. 4b). For the brain model that we have studied, the OSS‑weighted Helmholtz inversion resulted in higher resolution maps than the conventional Helmholtz inversion as observed in Figure 3. Consistent with our observations for the simulation brain data, human brain elastograms for OSS-weighted and conventional Helmholtz inversion results are similar but the OSS-weighted result seems sharper and more sensitive to rapid stiffness changes (Fig. 5), however, we do not know the ground truth. Based on significant improvements in the quality of elastography maps in two different inversion techniques, one may argue that this weighting can be useful for other inversion techniques. It is likely to observe more improvements when OSS weights are used with an inversion that does not assume local homogeneity.

Conclusion

It is concluded that using OSS-weighted averaging shows better performance than amplitude-weighted averaging or directly without any weighting. As future work, OSS weights should be used in an elasticity inversion technique that does not assume local homogeneity and the inversion should be tested on the data of brain or other tissues. Additionally, including Laplacian-SNR weights in the inversion can be compared with OSS‑weighted averaging because results in a recent study¹² imply that Laplacian-SNR weights may work better for elasticity inversion techniques that involves second derivative of the displacement field.

Acknowledgements

No acknowledgement found.

References

1. Papazoglou S, Hirsch S, Braun J, Sack I. Multifrequency inversion in magnetic resonance elastography. Phys Med Biol 2012;57:2329–2346 McCurry M et al., Elastojournal, 41(3): 724-33, 2015.

2. Tzschatzsch H , Guo J, Dittmann F, Hirsch S, Barnhill E, Johrens K, Braun J, Sack I. Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves. Med Image Anal2016;30:1–10

3. McGarry MDJ, Van Houten EEW, Perrinez PR, Pattison AJ, WeaverJB, Paulsen KD. An octahedral shear strain-based measure of SNR for 3D MR elastography. Phys Med Biol 2011;56:N153–N164

4. Ariyurek C, Tasdelen B, Ergun AS, Ider YZ, Atalar E. OSS-Weighted Averaging in Multifrequency Inversion for MR Elastography. 1st International MRE Workshop, Berlin Germany.

5. Aubert-Broche B, Evans AC, Collins L. A new improved version of the realistic digital brain phantom. NeuroImage. 2006 Aug 1;32(1):138-45.

6. “Brainweb: Simulated brain database, [online]. available: http://brainweb.bic.mni.mcgill.ca/brainweb/.”

7. McCracken PJ, Manduca A, Felmlee J, Ehman RL. Mechanical transient-based magnetic resonance elastography. Magn Reson Med 2005;53:628–639.

8. Ruan JS, Khalil T, King AI. Human head dynamic response to side impact by finite element modeling. Journal of Biomechanical Engineering. 1991 Aug 1;113(3):276-83.

9. Kleiven S, von Holst H. Consequences of head size following trauma to the human head. Journal of biomechanics. 2002 Feb 28;35(2):153-60.

10. Hamhaber U, Klatt D, Papazoglou, Sack I, Braun J. Simulation of wave fields observed in brain MR elastography by 3D finite element analysis. 17th Annual Meeting of ISMRM, Honolulu, Hawai'i, USA, 2009. p. 4349.

11. Dittmann F, Hirsch S, Tzschatzsch H, Guo J, Braun J, Sack I. In vivowideband multifrequency MR elastography of the human brain andliver. Magn Reson Med 2016;76:1116–1126

12. Manduca A, Lake DS, Huynh KT, Eon RS, Annoni EM, Ehman RL. Consistent SNR Measures for Magnetic Resonance Elastography. In Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Ontaria, Canada, 2015. p. 2519.

Figures

FIG. 1. (a) Geometry and dimensions of the simulation phantom. The plane on the top was vibrated sinusoidally, sweeping the excitation frequency from 24 to 48 Hz with steps of 4 Hz. White Gaussian noise (WGN) added complex displacement field data were exported with 2 mm isotropic voxels. (b) 3D brain model and direction of rotational vibration (similar to bite actuator). Excitation frequency was swept from 24 to 60 Hz with step of 4 Hz. WGN added complex displacement field data were exported with 1.5 mm isotropic voxels. (c) Geometry of the experiment phantom consisting 4 inclusions having different shear moduli.

FIG. 2. Shear wave speed maps, for the ground truth and obtained by k-MDEV inversion by amplitude weighted (conventional k-MDEV) and OSS-weighted averaging. Note that square root of OSS weights were used for OSS-weighted averaging since shear modulus is related with square of wave speed.

FIG. 3. Ground truth, conventional multifrequency Helmholtz inversion (no-weighting) and OSS-weighted Helmholtz inversion for the brain simulation data. Unlike k-MDEV inversion, OSS weights were used directly (i.e., without taking power) for OSS-weighted averaging. Differences between no-weighting and OSS-weighted inversions are observed mainly in sulci of the brain.

FIG. 4. For the experiment phantom: (a) Wave speed maps obtained by reconstructing data, acquired at different excitation frequencies, individually using k-MDEV. (b) The wave speed maps for the phantom data for amplitude-weighted (conventional k-MDEV) and OSS-weighted k-MDEV inversion. Cyan, yellow and pink ellipses demonstrate boundary artifacts, wave artifacts on the background and low visibility of the lower left inclusion, respectively.

FIG. 5. Conventional multifrequency Helmholtz inversion (no-weighting) and OSS-weighted Helmholtz inversion for healthy human experiment data. Differences between two images can be observed mainly in splenium of the corpus collosum and sulci, shown by the white arrows and the purple arrow, respectively. Stiff and anisotropic splenium of corpus callosum can be observed in OSS-weighted averaging inversion but it cannot be observed clearly in the inversion without weighting.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

1076