1022
Segmentation of Brain Tissues using a Bayesian Estimation of Multicomponent Relaxation Values in Magnetic Resonance Fingerprinting1Radiology, Case Western Reserve University, Cleveland, OH, United States, 2Radiology, University Hospitals, Cleveland, OH, United States
Synopsis
A Bayesian methodology has been previously applied to MRF reconstructions to analyze subvoxel T1 and T2 distributions. The multidimensional results from this algorithm are difficult to visualize. We propose to apply this Bayesian approach in the brain to create T1 and T2 Gaussian distributions to represent various tissue types. Using these distributions as prior information, the Bayesian methodology is applied over the brain with a smaller dictionary. Results from this Bayesian approach with a smaller dictionary are weighted by the Gaussian probabilities and summed to create tissue probability maps in normal volunteers and a brain tumor patient.
Purpose
The unique signal evolution structure in magnetic resonance fingerprinting (MRF)1 offers an opportunity to separate multiple components within a single voxel. Recent work on the Bayesian methodology for partial volume analysis in MRF2 shows that mixed signal evolutions can be separated with minimal prior information using a full MRF dictionary of simulated signal evolutions. This is especially important when one would like to segment an organ into specific tissue types. In this methodology, neither the number or types of subvoxel tissues need to be specified in advance, and the result is a distribution of tissue property values to explain the voxel composition, rather than one single set of effective tissue property values. One issue with this approach is the increased dimensionality of the solution over the traditional MRF tissue property maps, which makes visualization challenging. Additionally, when two tissues within a voxel have similar relaxation properties, for example, in white matter and gray matter, an approach that uses the full dictionary, such as this one2, may not be able to resolve these tissues clearly. Here we present a modification of the Bayesian methodology to provide tissue property probability maps, using prior information from targeted ROI analysis within the original Bayesian methodology for partial volume in normal volunteers and a brain tumor patient.Methods
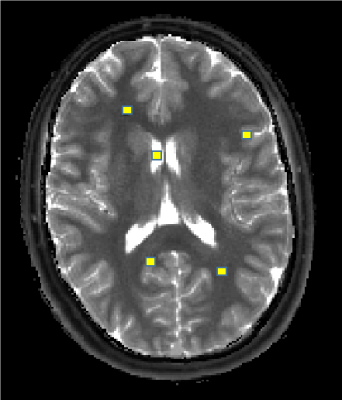
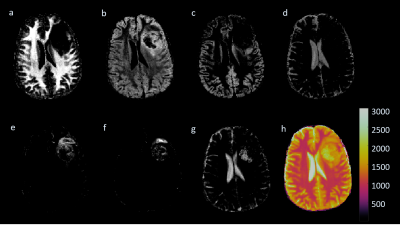
Two normal volunteers were scanned in an IRB-approved study at 3T using MRF-FISP3. Regions of interest (ROIs) were chosen in each volunteer for targeted subvoxel analysis using the full dictionary with the Bayesian approach. For the normal volunteers, regions were selected in pure white matter, gray matter, and CSF. The regions for one volunteer are shown in Figure 1. The T1, T2 results were combined across all regions, and a Gaussian mixture model was applied. Three Gaussians were selected by considering the maximum mixing probabilities of the distributions, which resulted in one distribution to model each tissue type. Using this ROI analysis as prior information, a smaller dictionary was formed, containing only the dictionary entries corresponding to the signal evolutions from the T1, T2 values that fell within the predefined distributions. Additionally, the maximum probability for each dictionary entry is saved, which indicates the distribution to which the entry is most likely to belong. This smaller dictionary for one volunteer contained 426 T1 and T2 combinations (compared to the full dictionary containing 5970) and was subsequently used in a multicomponent Bayesian analysis over the whole 2D slice. Results from this second analysis were again multidimensional. Tissue property probability maps were computed for the tissue types by computing a weighted sum of the the Bayesian result from the small dictionary multiplied with the precomputed tissue probabilities. Additionally, the method was applied to one patient who presented with a pathology-proved glioblastoma (GBM)4. This patient was scanned at 3T with MRF-bSSFP1. To account for pathological tissues, regions within the solid tumor and peritumoral white matter were also included in the initial ROI analysis.Results
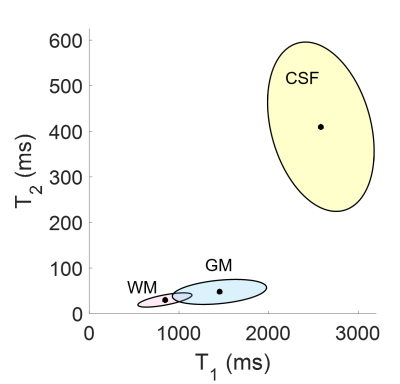
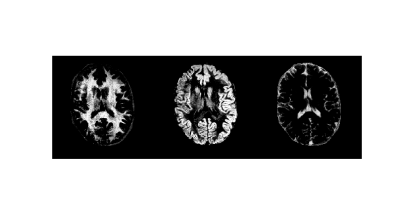
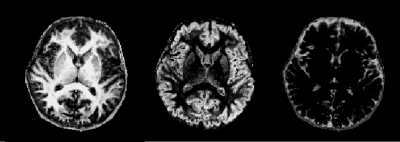
Figure 2 shows the Gaussian distributions as 95% credibility ellipses, formed from Bayesian subvoxel analysis on the ROIs from Figure 1. The distributions were computed by applying the expectation-maximization model for Gaussian mixture models. The distributions with the three largest final mixing probabilities were retained in the case of the normal volunteers, resulting in one distribution each to describe the three tissue types. Note that the standard deviation of the ellipses is impacted, in part, by the varying step size in the dictionary. For the patient, 10 Gaussians were generated, due to the question of the true T1 and T2 of the pathological tissues, and three were discarded due to low mixing probabilities. Probability maps for the normal volunteers are shown in Figures 3 and 4, and for the patient in Figure 5.Discussion and Conclusion
We present one possible solution to the visualization and interpretation of the results from a blind multicomponent analysis in MRF, such as the Bayesian analysis2 presented previously. We believe that this will have specific use in segmenting regions of the body into specific tissue types. One advantage of this approach is a significant savings in computation time, since after the initial ROI analysis utilizing the full dictionary, a smaller dictionary containing about one tenth of the number of entries can be used to compute the tissue property probability maps over the entire slice. A disadvantage of the approach is the inclusion of additional prior information into the Bayesian approach, which will clearly bias the solution based on the chosen ROIs. However, we believe that the SNR and clear definition of these tissues in the brain could lead to multiple applications, including surgical planning and the diagnosis of small gray matter lesions.Acknowledgements
The authors would like to acknowledge funding from Siemens and NIH grants 1R01EB016728-01A1 and 5R01EB017219-02.References
1. Ma, D. et al. Magnetic resonance fingerprinting. Nature 495, 187–192 (2013).
2. McGivney, D. et al. Bayesian estimation of multicomponent relaxation parameters in magnetic resonance fingerprinting. Magn. Reson. Med. (accepted).
3. Jiang, Y., Ma, D., Seiberlich, N., Gulani, V. & Griswold, M. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 74, 1621–1631 (2015).
4. Badve, C. et al. MR fingerprinting of adult brain tumors: Initial experience. Am. J. Neuroradiol. 38, 492-499 (2017).
Figures