0940
Joint SENSE Reconstruction for Faster Multi-Contrast Wave Encoding1Martinos Center for Biomedical Imaging, Charlestown, MA, United States
Synopsis
We introduce Joint SENSE acquisition/reconstruction to provide higher acceleration in multi-contrast acquisitions with improved image quality. We employ a complementary sampling strategy by shifting the k-space sampling patterns across the contrasts, which induces phase ramps in image space. By harnessing these ramps as additional coil sensitivity variations, we improve reconstruction error and g-factor performance by >2x compared to standard SENSE reconstruction. Further, we combine Joint SENSE with Wave encoding to exploit 4-dimensional sensitivity encoding, 3D across space + 1D across contrasts, to provide rapid multi-contrast acquisition with high quality.
Introduction
Multi-echo acquisitions are ubiquitous in clinical and research applications, with applications in T2/T2* parameter mapping, water-fat separation [1], BOLD sensitivity enhancement [2,3] and B0 field estimation [4]. Image information in these echoes feature substantial similarities, which can be leveraged using model-based reconstruction [5], joint-sparse and/or low-rank regularization [6,7].
Herein, we propose Joint SENSE, a complementary approach that exploits similarities between contrasts at the sensitivity encoding level. To this end, we shift the k-space sampling patterns of each echo, which creates phase ramps in image space. We then solve for each individual contrast using k-space data from all echoes, using new and additional coil sensitivities that include the incurred phase ramps. These help synthesize higher order Fourier harmonics, thereby substantially improving pRx capability. We demonstrate the application of joint reconstruction in Wave encoding [8], which now exploits 4-dimensional sensitivity encoding: 3D space + 1D contrast dimension.
Data / code: http://bit.ly/2hSHZDA
Theory
As shown in [Fig1, left], we incur k-space shifts between echoes during the multi-contrast acquisition. Due to Fourier shift theorem, shifted sampling creates a phase ramp in image $$$\rho$$$:
$$shift(F\cdot\rho)=F\cdot(\rho e^{j \cdot ramp})$$
where $$$F$$$ denotes
Fourier Transform and $$$e^{j \cdot ramp}$$$ represents the phase ramp. We employ these ramps for
extra spatial encoding. By stacking data from all contrasts in the coil axis,
we create additional channels and obtain the Joint SENSE forward model [Fig1, right]:
$$\left[\begin{array}{c} C_1\\ C_2\end{array}\right]\rho_1=\left[\begin{array}{c}C \cdot \rho_1\\ C \cdot \rho_2 e^{j\cdot ramp} \end{array}\right]$$
Here $$$\rho_1$$$ and $$$\rho_2$$$ are images with different contrasts, and $$$\rho_2$$$ has been shifted in k-space to incur $$$e^{j \cdot ramp}$$$. $$$C$$$ are the actual coil sensitivities (as in conventional SENSE [9]) and $$$C_1$$$ and $$$C_2$$$ are the unknown sensitivities that will be employed in Joint SENSE.
Sensitivities consistent with the forward model are $$$C_1 = C$$$ and $$$C_2 = C \cdot e^{j \cdot ramp} \cdot \frac{ \rho_2 } {\rho_1}$$$. This indicates that the incurred phase ramps are transferred to the additional coil sensitivities $$$C_2$$$, along with an undesired contrast-dependent term $$$\frac{ \rho_2 } {\rho_1}$$$. To mitigate its effect, we downweight the contribution from other contrasts with $$$\lambda$$$ to obtain the final Joint SENSE model:
$$\left[\begin{array}{c} F_\Omega C_1\\ \sqrt \lambda \cdot F_\Omega C_2\end{array}\right]\rho_1=\left[\begin{array}{c} kspace_1 \\ \sqrt \lambda \cdot kspace_2\end{array}\right]$$
where $$$F_\Omega$$$ is sub-sampled Fourier transform and $$$kspace_i$$$ are the acquired data from contrast $$$i$$$. We iteratively solve for $$$\rho_1$$$ using LSQR.
Data Acquisition and Reconstruction
Acquisitions were performed at 3T. Figs 2&3 employed conventional readout (without Wave) and 16 SVD compressed coils [10,11]. We explored Wave encoding in Fig4 with 24 SVD coils. $$$\lambda=5 \cdot 10^{-3}$$$ was used in all Joint SENSE/Wave reconstructions. Joint sensitivities $$$C_i$$$ were estimated automatically using ESPIRiT [12,13] after concatenating all echoes in the coil axis. G-factors were computed using 300 Monte-Carlo iterations [14].
Multi-Echo MPRAGE [15,16] [Fig2]: 1mm isotropic resolution, matrix=256x240x192, TEs={1.7, 3.6, 5.4, 7.3} ms, TR/TI=2500/1100 ms, BW=650 Hz/pixel. A slice along readout axis was undersampled by R=5x3-fold. K-space shifts for each echo in Joint SENSE were $$$(\Delta k_y, \Delta k_z)$$$=(0,0); (1,1); (2,2); (3,3).
Multi-Echo Spin-Echo [Fig3]: 0.9mm in-plane resolution, matrix=256x216,
TEs={30,50,60,75,90} ms, TR=800 ms, BW=130 Hz/pixel, R=5-fold acceleration. For
Joint SENSE, the five echoes were shifted by $$$\Delta k_y$$$={0,1,2,3,4}
samples.
Multi-Echo Wave MPRAGE [Fig4]: Using the dataset in Fig2, multi-echo Wave was simulated using 3 sinusoidal cycles, Slewmax=180mT/m/s, Gradientmax=14.6mT/m. Joint SENSE/Wave reconstructions were performed with $$$\Delta k_y$$$={0,1,2,3} shifts at R=4x3 acceleration.
Results
[Fig2]: Joint SENSE improved RMSE by >2-fold, and successfully mitigated noise amplification with average g-factor Gavg=1 compared to Gavg=2.8 in SENSE. Such improvement was possible thanks to additional sensitivity encoding and data averaging across echoes.
[Fig3]: Joint SENSE alleviated aliasing artifacts and noise amplification present in SENSE, with >2x improvement in RMSE and >4x in Gavg.
[Fig4]: Joint SENSE partially mitigated noise and artifacts in SENSE reconstruction, with 1.4x reduction in RMSE. Combining Joint reconstruction and Wave encoding in Joint Wave provided >2x error reduction with further quality improvement.
Discussion and Conclusion
Joint SENSE acquisition/reconstruction provides >2x improved RMSE and g-factor compared to standard SENSE. It can further be enhanced with low-rank and/or joint-sparse priors, and is flexibly extended to include Wave encoding. Joint Wave is particularly helpful in high-bandwidth ME-MPRAGE, where the readout period is too short to play a large Wave corkscrew, limiting the benefit from Wave encoding alone.
A drawback is the contrast
weighting in extra coil sensitivities, which was mitigated by downweighting
their contribution. This complicates Joint SENSE reconstruction of ME-GRE data
with large $$$\Delta$$$TE, where large phase differences between the echoes
counteract the effect of the added phase ramps. Phase navigator/ACS information
could help address this drawback.
Acknowledgements
This work was supported in part by NIH research grants: R01EB020613, R01EB019437, R24MH106096, P41EB015896, and the shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043.References
1. Reeder S, McKenzie C, Pineda A, Yu H, Shimakawa A, Brau AC, Hargreaves BA, Gold GE, Brittain JH. Water–fat separation with IDEAL gradient‐echo imaging. J. Magn. Reson. Imaging 2007;25.3:644–652.
2. Posse S, Wiese S, Gembris D, Mathiak K, Kessler C, Grosse-Ruyken M-L, Elghahwagi B, Richards T, Dager SR, Kiselev VG. Enhancement of BOLD-contrast sensitivity by single-shot multi-echo functional MR imaging. Magn. Reson. Med. 1999;42:87–97. doi: 10.1002/(SICI)1522-2594(199907)42:1<87::AID-MRM13>3.0.CO;2-O.
3. Poser B, Versluis M, Hoogduin J, Norris DG. BOLD contrast sensitivity enhancement and artifact reduction with multiecho EPI: parallel‐acquired inhomogeneity‐desensitized fMRI. Magn. Reson. Med. 2006;55.6:1227–1235.
4. Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn. Reson. Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111.
5. Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med. 2010;64:1114–1120. doi: 10.1002/mrm.22483.
6. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015;74:489–498. doi: 10.1002/mrm.25421.
7. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661. doi: 10.1002/mrm.25161.
8. Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 2015;73. doi: 10.1002/mrm.25347.
9. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962.
10. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn. Reson. Med. 2007;57:1131–1139. doi: 10.1002/mrm.21237.
11. Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn. Reson. Imaging 2008;26:133–141. doi: 10.1016/j.mri.2007.04.010.
12. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001. doi: 10.1002/mrm.24751.
13. Uecker M, Virtue P, Vasanawala SS, Lustig M. ESPIRiT Reconstruction Using Soft SENSE. In: Proceedings of the 21st Annual Meeting ISMRM. ; 2013. p. 127.
14. Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, McKenzie CA. Comprehensive quantification of signal-to-noise ratio and g -factor for image-based and k -space-based parallel imaging reconstructions. Magn. Reson. Med. 2008;60:895–907. doi: 10.1002/mrm.21728.
15. Mugler JP, Brookeman JR. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE). Magn. Reson. Med. 1990;15:152–157. doi: 10.1002/mrm.1910150117.
16. van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025.
Figures
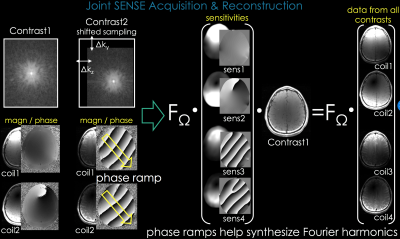
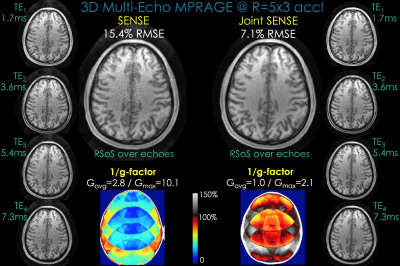
Fig2. [Left] Standard SENSE reconstruction for multi-echo MPRAGE acquisition at R=15-fold acceleration. Both individual echoes and the RSoS combined image suffer from severe noise amplification and artifacts, as quantified by the g-factor analysis and RMSE (Gavg=2.8, 15.4% error). [Right] Joint SENSE provides >2x improvement in g-factor and RMSE, with substantially improved image quality. We note that despite achieving Gavg=1.0 thanks to noise averaging across echoes, the intrinsic sqrt(R) penalty on SNR due to undersampling still impacts the reconstruction.
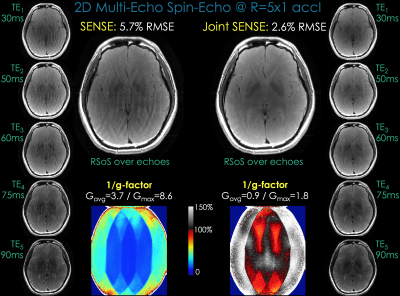
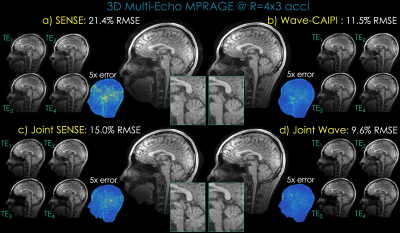
Fig4. a) Multi-echo MPRAGE with standard SENSE reconstruction at R=4x3 (As in Fig2, Ry and Rz are along anterior-posterior and left-right directions, with readout lying along head-foot). SENSE suffered large RMSE, in part due to low receiver sensitivity and low signal in the nasal cavity/mouth regions in this sagittal view. b) Wave-CAIPI spreads the aliasing in 3D to improve RMSE and SNR retention. c) Joint SENSE utilizes the additional sensitivity encoding through shifted sampling, yet yields worse performance than Wave encoding alone. d) Combination of Wave and Joint SENSE is powerful, providing >2x RMSE improvement and cleaner reconstruction.