0939
Self-calibrating Wave-encoded 3D Turbo Spin Echo Imaging using Subspace Model based Autofocus1Philips Research North America, Cambridge, MA, United States, 2Vascular Imaging Lab, Department of Radiology, University of Washington, Seattle, WA, United States, 3Center for Biomedical Imaging Research, Department of Biomedical Engineering, Tsinghua University, Beijing, China, 4Philips Research Hamburg, Hamburg, Germany
Synopsis
Wave-encoding techniques can better utilize the three-dimensional (3D) encoding power of parallel imaging (PI) during acquisition and image reconstruction, but proper calibration of wave point spread function (PSF) and coil sensitivities are required. In this study, a self-calibrating wave PSF and PI kernel approach from subsampled wave-encoded k-space is proposed using subspace model based autofocus estimation. Its performance is evaluated for 3D wave encoded turbo spin echo (TSE) imaging. The preliminary results on phantom has demonstrated the calibration accuracy of self-calibrated wave PSF and improved PI performance in comparison to Cartesian based PI for 3D TSE imaging.
Introduction
Wave-encoding techniques can optimize the aliasing/folding properties in case of undersampled parallel imaging (PI) by better conditioning the unfolding problem1. So the entire three-dimensional (3D) encoding power of multi-channel MRI can be used supporting accelerated volumetric imaging2,3 or simultaneous multi-slice imaging4,5. But proper calibration of the wave point spread function (PSF) and the coil sensitivity/PI kernel is required before image reconstruction of subsampled wave-encoded k-space dataset. Recently, several auto-calibrating methods3,6 have been developed instead of using pre-scan methods to improve the calibration accuracy. But either wave PSF or coil sensitivities are still required to calibrate the other unknown parameters. The latest self-calibrating method7 has demonstrated the feasibility of joint wave PSF and coil sensitivities calibration from the subsampled k-space for two-dimensional wave-encoded turbo spin echo (TSE) imaging. In this study, a subspace model based autofocus method is developed as another self-calibrated wave-encoding approach, and its performance is evaluated for 3D wave encoded TSE imaging.Methods
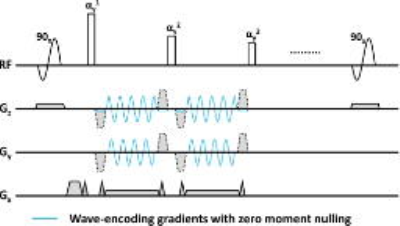
Wave-encoded 3D TSE sequence: A pair of sine and cosine gradient waveforms are applied in the phase- and slice-encoding directions during the regular Cartesian readout for wave-encoded k-space acquisition (figure 1). Eddy current compensation is considered in the implementation of wave-encoding gradients. To comply with the Carr-Purcell-Meiboom-Gill condition, the zeroth moment of compensated sinusoidal gradients are further nulled by a pair of prephasing and rephasing gradients within each echo spacing.
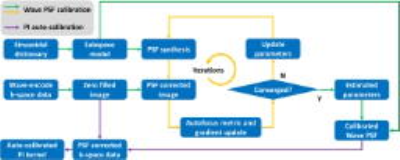
Subspace model based autofocus for wave PSF self-calibration: Image based autofocus metric can measure how much residual artifacts still exist on the PSF corrected image given the current parameters $$$C_y$$$, $$$C_z$$$, and $$$p$$$ in PSF ($$$PSF\left(k_x,y,z;C_y,C_z,p\right) = exp\left(-j2\pi\left(C_y\left(k_x\right)\left(y-p_y\right)+C_z\left(k_x\right)\left(z-p_z\right)\right)\right)$$$). To effectively reduce the parametric searching space for $$$C_y$$$ and $$$C_z$$$, a subspace model can be established by applying singular value decomposition on a simulated dictionary consisting of a group of sine functions with various periods and phases, which also provides certain robustness to gradient system imperfection. Also, the selection of autofocus metric plays a critical role for calibration accuracy of PSF parameters8. Image intensity based entropy and the L1-norm of image intensity gradient are two candidate autofocus metrics evaluated in this study. The quasi-newton method is used to iteratively minimize the autofocus metric for wave PSF estimation as illustrated in figure 2.
PI kernel calibration and image reconstruction: With the calibrated wave PSF, the zero filled wave-encoded k-space can be corrected to approximate the Cartesian k-space. The SPIRiT9 kernel $$$G$$$ can be calibrated from this approximated central k-space (figure 2). Then the subsampled wave-encoded k-space can be reconstructed by solving $$$\min_{v}\|\left(G-I\right)F_{yz}PSF^HF_{yz}^H\left(D^Tu+D_c^Tv\right)\|_2^2$$$, where $$$u$$$/$$$v$$$ is the acquired/unacquired wave-encoded data, $$$D^T$$$/$$$D_c^T$$$ operator projects the entries in the input data vector onto the acquired/unacquired coordinates in wave-encoded k-space, $$$F_{yz}$$$/$$$F_{yz}^H$$$ operator is the Fourier/inverse Fourier transform along the y and z directions.
MR experiments: The fully sampled wave-encoded and Cartesian phantom datasets were acquired by a 32-channel head coil on Philips Ingenia 3.0T scanner using the 3D TSE sequence (FOV = 210x210x50mm3, resolution = 1x1x2mm3, TE/TR = 21ms/800ms) with or without wave-encoding gradients (6mT/m, 4 cycles). The acquired datasets were retrospectively subsampled with a 25x25 central calibration area and different undersampling patterns in peripheral k-space. Coil compression10 was performed to improve the computational efficiency.
Results
Impact of autofocus metric: If the wave PSF can be calibrated from fully sampled wave-encoded k-space, both investigated autofocus metrics can provide accurate PSF correction. However, the image entropy autofocus metric might result in underestimation of the trajectory parameters when it comes to the calibration from subsampled wave-encoded k-space, leading to residual artifacts (red arrows in figure 3). In contrast, the L1-norm of image gradient autofocus metric can provide more robust PSF calibration even in the undersampling situation.
PI reconstruction performance: For variable density sampling with 5-fold acceleration, SPIRiT reconstruction can provide comparable image quality for subsampled Cartesian and wave-encoded k-space. However, if the undersampling pattern is not in a good condition, considering the 3-fold uniform undersampling as an example, wave-encoding can better suppress the aliasing artifacts occurred in Cartesian-encoding (red arrows in figure 4).
Discussion and Conclusion
The autofocus motion correction framework8,11 has been successfully adapted for accurate wave PSF calibration in a self-calibrating fashion by creating a low-rank subspace model and optimizing the autofocus metric. The developed self-calibrating autofocus method has the potential to be applied for other wave-encoded 3D imaging sequences. Also, the self-calibrated trajectories imply the effective implementation of wave-encoding gradients for 3D TSE sequence. With the developed self-calibrating wave PSF and PI kernel approach, wave-encoded PI has demonstrated comparable/superior performance in comparison to Cartesian PI for 3D TSE imaging.Acknowledgements
No acknowledgement found.References
1. Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn Reson Med. 2015;73(6):2152-62.
2. Polak D, Setsompop K, Cauley SF, Gagoski BA, Bhat H, Maier F, Bachert P, Wald LL, Bilgic B. Wave-CAIPI for highly accelerated MP-RAGE imaging. Magn Reson Med. 2017. Epub.
3. Chen F, Zhang T, Cheng JY, Shi X, Pauly JM, Vasanawala SS. Autocalibrating motion-corrected wave-encoding for highly accelerated free-breathing abdominal MRI. Magn Reson Med. 2017;78(5):1757-1766.
4. Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL, Setsompop K. RARE/turbo spin echo imaging with Simultaneous Multislice Wave-CAIPI. Magn Reson Med. 2015;73(3):929-38.
5. Poser BA, Bilgic B, Gagoski BA, Uludag K, Stenger VA, Wald LL, Setsompop K. Echo-Planar Imaging with Wave-CAIPI Acquisition and Reconstruction. ISMRM 2017. p1198.
6. Cauley SF, Setsompop K, Bilgic B, Bhat H, Gagoski B, Wald LL. Autocalibrated wave-CAIPI reconstruction; Joint optimization of k-space trajectory and parallel imaging reconstruction. Magn Reson Med. 2017;78(3):1093-1099.
7. Chen F, Taviani V, Tamir JI, Cheng JY, Zhang T, Song Q, Hargreaves BA, Pauly JM, Vasanawala SS. Self-Calibrating Wave-Encoded Variable-Density Single-Shot Fast Spin Echo Imaging. J Magn Reson Imaging. 2017. Epub.
8. McGee KP, Manduca A, Felmlee JP, Riederer SJ, Ehman RL. Image metric-based correction (autocorrection) of motion effects: analysis of image metrics. J Magn Reson Imaging. 2000;11(2):174-81.
9. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010;64(2):457-71.
10. Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imaging 2008;26:133–141.
11. Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. Nonrigid motion correction in 3D using autofocusing with localized linear translations. Magn Reson Med. 2012;68(6):1785-97.
Figures