Synopsis

Variable density sampling is now commonly used in advanced imaging methods. However, due to ill conditioning, reconstruction can take hundreds of iterations, limiting its clinical application. One effective heuristic to accelerate convergence is the use of density compensation, but it is known to increase reconstruction error. An alternative is to use preconditioners, but existing preconditioners increase computation by performing additional image convolutions. Our goal here is to accelerate iterative reconstruction convergence without compromises. We propose a k-space diagonal preconditioner, without compromising reconstruction error, or computation. We demonstrate on datasets that reconstructions with the proposed preconditioner converge at around 10 iterations.

Introduction

Variable density sampling (VDS)¹ is now commonly used in advanced imaging methods, including most non-Cartesian, and compressed sensing² trajectories. While providing benefits such as motion robustness, and energy adaptiveness, reconstruction from VDS is more ill-conditioned than from uniform sampling. This ill-conditioning appears as blurring in reconstruction, and can require hundreds of iterations to resolve, limiting its clinical application.

One effective heuristic to accelerate convergence is density compensation³, but at the cost of increased reconstruction error, as densely sampled region is weighted down in data consistency. An alternative is to use preconditioners, but existing preconditioners^4-6 appear as image convolution, which increases computation.

Our goal here is to accelerate iterative reconstruction convergence for VDS without compromises. We propose a k-space preconditioner to achieve this, while retaining the computational efficiency of density compensation.

Theory

Problem setup

Concretely, let $$$A$$$ be the multi-channel encoding matrix which includes sensitivity maps and Fourier transform, $$$x$$$ be the underlying image, and $$$y$$$ be the acquired k-space measurements, we consider the following objective function:

$$\min_x\frac{1}{2}\|Ax-y\|_2^2+g(x)$$

where $$$g(x)$$$ is the regularization function.

Applying the proximal gradient method, for example, gives the following update: $$x^{n+1}=\text{prox}_{\alpha g}(x^n-\alpha A^*(Ax^n-y))$$

where $$$\alpha$$$ is the step-size, and $$$\text{prox}$$$ is the proximal operator. For VDS, $$$A$$$ can be very ill-conditioned, requiring hundreds of iterations to converge.

Density compensation

One effective heuristic to accelerate convergence for VDS is the use of density compensation factors (DCF). Given a diagonal matrix $$$D$$$ with DCF as diagonals, proximal gradient method is modified to:

$$x^{n+1}=\text{prox}_{\alpha g}(x^n-\alpha A^*D(Ax^n-y))$$

However, such k-space weighting is known to increase reconstruction errors, as implicitly it solves for the weighted objective function:

$$\min_x\frac{1}{2}\|\sqrt{D}(Ax-y)\|_2^2+g(x)$$

Note that data consistency is weighed down in densely sampled regions, so measurements are essentially thrown away for convergence, resulting in increased reconstruction error, and noise coloring.

Image-domain preconditioning formulation

An alternative is to use preconditioners, which only affect the convergence, but not the converged result. However, conventional preconditioning^4-6 applies on the variable directly, and can only be applied in image domain. For instance, given a preconditioner $$$P$$$, the proximal gradient method applies:

$$x^{n+1}=\text{prox}_{\alpha g, P}(x^n-\alpha PA^*(Ax^n-y))$$

This poses a mismatch, as the preconditioner tries to compensate for VDS in image domain. Conventional preconditioners appear in the form of image convolution, which increases computation. Moreover, the proximal operator must be updated to incorporate preconditioner, which can involve solving another iterative reconstruction.

Proposed k-space diagonal preconditioning formulation

Our key observation is that the dual objective function operates in k-space, and can be preconditioned in k-space. In particular, the dual objective function is given by:

$$\max_u-\left(\frac{1}{2}\|u\|_2^2+y^*u+g^*(-A^*u)\right)$$

where $$$g^*$$$ denotes the convex conjugate function of $$$g$$$.

Since the dual variable $$$u$$$ operates in k-space, we can use diagonal k-space preconditioners to accelerate convergence. We note that in the special case of conjugate gradient, this property is observed by Trzasko et al⁷.

We propose to use the first order primal-dual method⁸, with preconditioning⁹, which allows us to update the dual and primal variable at the same time:

$$u^{n+1}=(I+\sigma P)^{-1}(u^n+\sigma P(A(2x^n - x^{n-1})+y))$$

$$x^{n+1}=\text{prox}_{\tau g}(x^n-\tau A^*u^{n+1})$$

where $$$\tau$$$ and $$$\sigma$$$ are the step-sizes. The pre-iteration computational complexity is similar to that of conventional proximal gradient method.

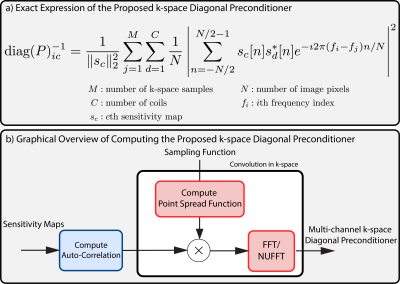
Proposed $$$\ell2$$$ optimized k-space diagonal preconditioner

While existing DCFs can be used as k-space diagonal preconditioners, they were not designed for iterative reconstruction, and might not improve convergence. We propose to use a diagonal preconditioner to approximate the inverse of the normal operator $$$AA^*$$$ in the least squares sense, that is,

$$P=\text{argmin}_{P\text{diagonal}}\|PAA^*-I\|_F^2$$

Due to limited space, we cannot include a detailed derivation, and refer the reader to Figure 1 for more detail. We note that the preconditioner can be calculated efficiently using FFT/NUFFT's.

One key difference between our proposed preconditioner and DCF is that for multi-channel, our proposed preconditioner applies different weighting for each channel, which provides extra degrees of freedom to accelerate convergence.

Results

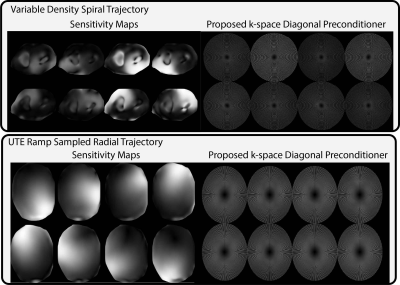
We evaluated our proposed k-space preconditioner on two VDS datasets, one acquired with a 2D variable density spiral trajectory, and another with a 2D UTE ramp sampled radial trajectory. Figure 2 shows their corresponding sensitivity maps estimated using ESPIRiT¹⁰, and the proposed preconditioners.

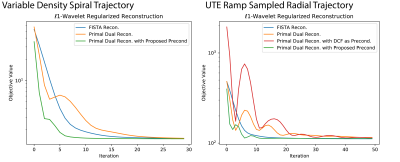
Figure 3 shows the objective values over iterations comparing FISTA, first-order primal dual, and first-order primal dual with the proposed preconditioner. We also compared reconstruction using Pipe et al.'s DCF⁴ as a preconditioner for the UTE dataset. In both cases, reconstruction with the proposed k-space preconditioner achieves the fastest convergence.

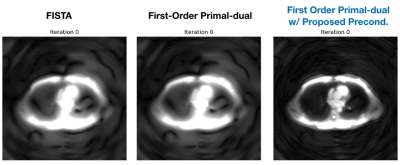
Figure 4, and 5 show the iteration images. The results show that the proposed k-space preconditioner speeds up iteration convergence, and essentially produces converged results around 10 iterations.

Conclusion

Acknowledgements

References

[1] Tsai, C.M. and Nishimura, D.G., 2000. Reduced aliasing artifacts using variable‐density k‐space sampling trajectories. Magnetic resonance in medicine, 43(3), pp.452-458.

[2] Lustig, M., Donoho, D. and Pauly, J.M., 2007. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic resonance in medicine, 58(6), pp.1182-1195.

[3] Pipe, J.G. and Menon, P., 1999. Sampling density compensation in MRI: rationale and an iterative numerical solution. Magnetic resonance in medicine, 41(1), pp.179-186.

[4] Ramani, S. and Fessler, J.A., 2011. Parallel MR image reconstruction using augmented Lagrangian methods. IEEE Transactions on Medical Imaging, 30(3), pp.694-706.

[5] Muckley, M. J., et al. "Fast, Iterative Subsampled Spiral Reconstruction via Circulant Majorizers." In Proceedings of the 24th Annual Meeting of ISMRM 2016, Singapore #0521.

[6] Koolstra, Kirsten, et al. "Accelerating CS in Parallel Imaging Reconstructions Using an Efficient and Effective Circulant Preconditioner." arXiv preprint arXiv:1710.01758 (2017).

[7] Trzasko, J. D., et al. "A Preconditioned ADMM Strategy for Field-Corrected Non-Cartesian MRI Reconstruction." In Proceedings of the 22nd Annual Meeting of ISMRM 2014, Milan, Italy #1535.

[8] Chambolle, A., and Pock. T. "A first-order primal-dual algorithm for convex problems with applications to imaging." Journal of mathematical imaging and vision 40.1 (2011): 120-145.

[9] Pock, T., and Chambolle. A. "Diagonal preconditioning for first order primal-dual algorithms in convex optimization." Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011.

[10] Uecker, M., Lai, P., Murphy, M.J., Virtue, P., Elad, M., Pauly, J.M., Vasanawala, S.S. and Lustig, M., 2014. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine, 71(3), pp.990-1001.