0920

Improved Design and Reconstruction of 3D Image Based Navigators for Coronary MR Angiography
Mario O. Malavé1, Srivathsan P. Koundinyan1, Christopher M. Sandino1,2, Joseph Y. Cheng1,2, and Dwight G. Nishimura1

1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Palo Alto, CA, United States

Synopsis

We present a novel method to acquire whole-heart 3D image-based navigators (iNAVs) for tracking and correction of localized motion in free-breathing coronary angiography. More specifically, a variable-density, phyllotaxis-based trajectory is utilized for homogeneous sampling of the desired k-space extent. To reconstruct the 3D iNAVs, a locally low rank regularized iterative scheme is implemented. Across all volunteer studies, compared to 3D iNAVs generated with prior design and reconstruction strategies, the proposed 3D iNAVs provide superior delineation of the structures of interest. Application of the proposed 3D iNAVs for motion correction in volunteer studies yields improved depiction of the coronary arteries.

Introduction

We present a novel method to acquire and reconstruct whole-heart 3D image-based navigators (iNAVs) for retrospective motion correction in coronary magnetic resonance angiography (CMRA). 3D iNAVs are collected every heartbeat using a variable-density, conical phyllotaxis trajectory. Reconstruction is performed using a locally low rank (LLR) regularized iterative scheme. Compared to 3D iNAVs reconstructed with other design and reconstruction strategies, applying the proposed 3D iNAVs provides equivalent or better depiction of the coronary arteries.

Methods

Cardiac-triggered, free-breathing CMRA data (28x28x14 cm3 FOV, 1.2 mm isotropic spatial resolution, 610 heartbeats total scan time) are acquired on a 1.5T GE Signa system with an 8-channel cardiac coil and a 3D cones trajectory1. For localized motion estimation, 3D iNAV data (28x28x14 cm3 FOV, 176 ms temporal resolution, 4.4 mm isotropic spatial resolution) is collected every heartbeat after the imaging segment with 32 variable-density cone readouts (undersampled), yielding an acceleration factor of 9 (Figure 1(a)).

3D iNAV Design

In general, cone readouts are parameterized by a set of azimuthal angles $$$(\phi\ \epsilon\ (0, 2π))$$$ and elevation angles $$$(\theta\ \epsilon\ (-π/2, π/2))$$$. Readouts follow an initial radial path and traverse thereafter in a spiral-like fashion along a conic surface. Prior design of 3D iNAVs restricted the 32 readouts to 18 finite surfaces spanning the full range of elevation angles2. Within a designated surface, between 1 to 3 cones were equally separated in the azimuthal direction. Across all heartbeats, the same locations in k-space were sampled.

In the proposed 3D iNAV acquisition scheme, two modifications are implemented (Figure 1(b-d)):

  1. Each readout is assigned a unique elevation angle using the phyllotaxis technique in [3]. Compared to the prior design, this approach provides more homogeneous sampling of the same k-space extent and reduces the changing of gradients between adjacent cone readouts. These improvements can alleviate artifacts arising from eddy current effects. To further promote uniformity, adjacent cone readouts are separated in the azimuthal direction by the golden angle.
  2. The 3D iNAV trajectories across all heartbeats cover unique locations in the desired k-space range. Specifically, the 32 readouts for a heartbeat are an azimuthally rotated version (i.e., golden angle rotation) of the 32 readouts from the prior heartbeat.

3D iNAV Reconstruction

Prior work reconstructed 3D iNAVs independently of one another using L1-ESPiRIT2. Design modification (2) above introduces incoherent undersampling artifacts between the 3D iNAVs from each heartbeat. We leverage this benefit and exploit temporal redundancy to jointly reconstruct 3D iNAVs for each heartbeat using an LLR regularized iterative framework4:

$$\underset{M_{lr}}{\operatorname{argmin}}\DeclareMathOperator*{\argmin}{arg\,min}\lVert DSM_{lr} - y_{lr}\rVert_2^2 + \lambda\sum_{i\in\Omega}\lVert L_{i}M_{lr}\rVert_*$$

where $$$D$$$ is the NUFFT operator, $$$S$$$ contains the coil sensitivity maps, $$$M_{lr}$$$ (3D spatial + 1D temporal: nx x ny x nz x nt) is the set of 610 3D iNAVs, $$$y_{lr}$$$ is the corresponding non-Cartesian data, and $$$λ$$$ is the regularization parameter. The regularization term minimizes the nuclear norm of $$$M_{lr}$$$ after it has been split into block sizes of 8 x 8 x 8 x 610. $$$Ω$$$ denotes the set of all blocks, and the $$$L_{i}$$$ operator reformats each block into its Casorati matrix. FISTA and singular value thresholding are used to solve the above optimization problem5. $$$λ$$$ is empirically chosen to be 0.01 in this work.

The 3D iNAVs generated with the proposed framework are processed for motion correction using the technique in [6]. Here, 32 3D translational motion estimates are extracted from different ROIs on the 3D iNAVs, and independently applied to reconstruct a bank of motion-compensated images. Minimization of a gradient entropy metric across the 32 translationally corrected images yields the final image7,8.

Results

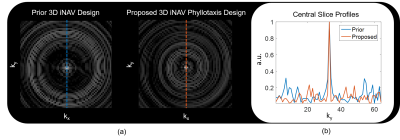
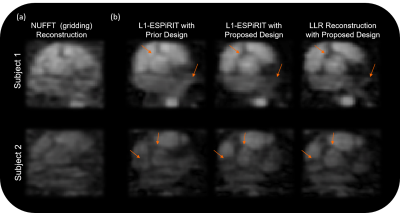
Analysis of the point spread function for the prior and proposed iNAV acquisition technique demonstrates the improvements offered by the latter (Figure 2). Figure 3 showcases example 3D iNAVs generated with three different schemes: (1) the prior design and L1-ESPiRIT reconstruction, (2) the proposed design and L1-ESPiRIT reconstruction, and (3) the proposed design and LLR reconstruction. Depiction of salient structures in the heart improves from scheme (1) to (2), with scheme (3) presenting the most detail. 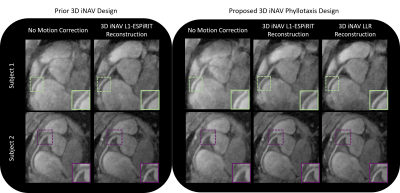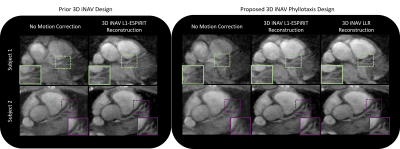The 3D iNAVs formed with the three techniques are assessed in two free-breathing CMRA exams (Figures 4 and 5). For subject 1, the depiction of the right and left coronary arteries is the sharpest when applying scheme (3). For subject 2, vessel sharpness is equivalent in schemes (2) and (3).

Discussion and Conclusion

We have presented an improved method to design and reconstruct a variable-density cones trajectory for rapid 3D iNAV acquisition. Application of the proposed method in free-breathing CMRA exams provides improved or similar image quality compared to prior design and reconstruction strategies.

Acknowledgements

We gratefully acknowledge the support of NIH grants R01HL127039, T32HL007846, and T32EB009653. This work was also supported by the Hsi-Fong Ho Stanford Graduate Fellowship, the Ruth L. Kirschstein National Research Award, and the National Science Foundation Graduate Research Fellowship under Grant No. DGE-114747.

References

  1. Wu, Holden, et al. "Free‐breathing multiphase whole‐heart coronary MR angiography using image‐based navigators and three‐dimensional cones imaging." Magnetic resonance in medicine 69.4 (2013): 1083-1093.
  2. Addy, Nii Okai, et al. "High‐resolution variable‐density 3D cones coronary MRA." Magnetic resonance in medicine 74.3 (2015): 614-621.
  3. Malave, Mario, et al. "3D Cones reordering design methods for whole-heart coronary MR angiography." Proceedings of the international society for magnetic resonance in medicine (2015).
  4. Jiang, Wenwen, et al. "Motion robust high resolution 3D free‐breathing pulmonary MRI using dynamic 3D image self‐navigator." Magnetic resonance in medicine (2017).
  5. Berkeley Advanced Reconstruction Toolbox (BART): https://mrirecon.github.io/bart/
  6. Koundinyan, Srivathsan, et al. "Quantification, analysis, and correction of nonrigid motion in free-breathing, non-contrast-enhanced renal magnetic resonance angiography." Proceedings of the international society for magnetic resonance in medicine (2017).
  7. Cheng, Joseph, et al. "Nonrigid motion correction in 3D using autofocusing with localized linear translations." Magnetic resonance in medicine 68.6 (2012): 1785-1797.
  8. Ingle, R. Reeve, et al. "Nonrigid autofocus motion correction for coronary MR angiography with a 3D cones trajectory." Magnetic resonance in medicine 72.2 (2014): 347-361.

Figures

Figure 1: (a) Timing diagram for free-breathing CMRA acquisition scheme. 3D iNAVs are collected every heartbeat following fat saturation and imaging data acquisition. (b) 3D iNAVs are acquired using a variable-density, undersampled 3D cones trajectory. Prior design of 3D iNAVs exhibits non-uniform separations of the conical surfaces in the desired k-space extent. (c) The proposed design employs a phyllotaxis scheme to improve the homogeneity of the collected points. In addition, between heartbeats, the proposed design rotates the trajectory (d) by the golden angle to increase the incoherency of the undersampling artifacts among the 3D iNAVs.

Figure 2: NUFFT (gridding) is used to generate each point spread function (PSF) in (a). There are notable differences in the PSF between the prior and proposed 3D iNAV design techniques. For example, the sidelobes exhibit higher energy in the PSF for the prior design compared to the proposed design. In addition, the width of the main lobe is smaller for the phyllotaxis scheme (b).

Figure 3: (a) NUFFT (gridding) of the 32 acquired cones for a 3D iNAV yields an aliased image (cropped). (b) Utilization of L1-ESPiRIT with the prior design of 3D iNAVs removes many of the aliasing artifacts (left). Incorporation of the proposed phyllotaxis design further highlights structures of interest (middle). The sharpest features are present in the 3D iNAVs formed with the proposed design and LLR reconstruction (right).

Figure 4: 3D iNAVs collected using the prior design and proposed design, and reconstructed with (1) no motion correction, (2) L1-ESPiRIT, and (3) LLR are evaluated in two free-breathing volunteer studies. The right coronary artery is sharpest for subject 1 when utilizing 3D iNAVs acquired with the proposed design and reconstruction strategy. In subject 2, 3D iNAVs reconstructed with L1-ESPIRiT perform similarly to those reconstructed with an LLR framework. In both studies, the degree of improvement in vessel depiction from no motion correction appears higher when utilizing 3D iNAVs acquired with the proposed design compared to the prior design.

Figure 5: For subject 1, the left coronary artery is notably sharper when using 3D iNAVs collected with proposed design and reconstructed with an LLR scheme. In subject 2, 3D iNAVs collected with proposed design and reconstructed with L1-ESPiRIT effectively mitigate motion artifacts. The LLR reconstruction strategy yields similar results. It is important to note that 3D iNAVs reconstructed with LLR perform equivalently, if not superiorly, to those reconstructed with L1-ESPiRIT.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0920