Synopsis

Dynamic 31P-MRS/MRSI is often used to assess mitochondrial oxidative capacity in skeletal muscle by monitoring the depletion and recovery of the phosphocreatine concentration during ischemia-reperfusion experiments. In animal models, standard methods are unable to provide the spatiotemporal resolution needed to discern spatial heterogeneity of the recovery process ($$$<$$$10 s/frame, $$$\approx$$$1 mm³ per voxel). To address this problem, we have improved a recently proposed low-rank tensor based method for accelerated high-resolution dynamic 31P-MRSI to provide in vivo results with 1.5x1.5x2 mm³ nominal spatial resolution, 36 ppm spectral bandwidth, 0.14 ppm spectral resolution, and 5.1 s temporal resolution.

Introduction

Mitochondrial oxidative capacity in skeletal muscle can be assessed by monitoring the depletion and recovery of the phosphocreatine (PCr) concentration during ischemia-reperfusion experiments. Dynamic 31P-MRS/MRSI is often the tool of choice for these experiments^1-3 because it can provide non-invasive, in-vivo measurements of the concentrations of PCr as well as ATP and inorganic phosphate. In small animal models such as rats, the time constant of PCr recovery is approximately 60 s. Hence, a temporal resolution of less than 60 s is necessary to capture the kinetics of PCr recovery. Furthermore, the spatial resolution should be on the order of 1 mm³ if spatial heterogeneity is to be observed. Unfortunately, due to the inherently low SNR of the 31P-NMR signal, dynamic 31P-MRSI methods with adequate temporal resolution are typically limited to very low spatial resolution (on the order of 1 cm³).

Much work has been done to provide better combinations of spatial and temporal resolution^4-8. Recently, a tensor-based method was introduced for providing dynamic 31P-MRSI reconstructions, achieving a resolution on the order of 1 mm³ and approximately 30 s temporal resolution⁹. However, for robust estimation PCr recovery rates, it is desirable to have temporal resolutions of less than 10 s. Therefore, in this work we present results from a modified acquisition and reconstruction framework which provides a factor of 6x acceleration compared to the previous work. Specifically we present results from 3 in vivo ischemia-reperfusion experiments on rat hindlimbs with 1.5x1.5x2 mm³ nominal spatial resolution, 36 ppm spectral bandwidth, 0.14 ppm spectral resolution, and 5.1 s temporal resolution.

Methods

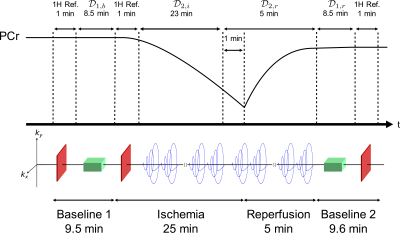
In vivo data from three Sprague-Dawley rats were acquired on a 9.4T Bruker Biopic horizontal scanner. Each rat was anesthetized and had an inflatable cuff placed around its thigh. A Bruker 1H volume coil was used for shimming and the acquisition of the proton reference scans. A custom 31P saddle coil was placed around the animal's calf muscles to acquire MRSI data. The pressure cuff was inflated and deflated according to Fig. 1.

For each animal, we acquired two spectral subspace navigators, $$$\mathcal{D_{1,b}}$$$, $$$\mathcal{D_{1,r}}$$$, and two dynamic imaging acquisitions $$$\mathcal{D_{2,i}}$$$, $$$\mathcal{D_{2,r}}$$$ as shown in Fig. 1. $$$\mathcal{D_{1,b}}$$$ and $$$\mathcal{D_{1,r}}$$$ were acquired using a CSI-FID sequence with a 8x8x6 matrix size, 6 kHz readout bandwidth, 256 samples per readout and 8 averages. $$$\mathcal{D_{2,i}}$$$ was acquired with a 16x16x8 matrix size (stack of uniform density spirals), 90 kHz readout bandwidth, 4.66 ms echo-spacing, 17 echoes, and 4 averages, which corresponded to a nominal resolution of 1.5x1.5x2 mm³ with a FOV of 24x24x16 mm³ and a 5.1 s frame rate with a TR of 160 ms. $$$\mathcal{D_{2,r}}$$$ was similar to $$$\mathcal{D_{2,i}}$$$ except that it had 111 kHz readout bandwidth, 3.78 ms echo-spacing, and 20 echoes ($$$\mathcal{D_{2,i}}$$$ was designed with weaker gradients to reduce gradient heating during the long ischemia period). For all acquisitions the FOV, TR/TE, and flip angle were the same (TE = 0.69 ms, flip angle = 17 degrees). The total duration of each experiment was approximately 49.1 minutes.

The dynamic MRSI image was reconstructed by solving the following optimization problem:$$\begin{matrix}\{\hat{\upsilon}_m(\mathbf{x},T)\}_{m=1}^M &=&\ \arg\min\limits_{\{\upsilon_m\}_{m=1}^M}\left\Vert \mathbf{d}-\mathcal{F}\left\{r(\mathbf{x})\sum_{m=1}^M\upsilon_{m}\left(\mathbf{x},T\right) \hat{\phi}_m\left(f\right)\right\}\right\Vert_2^2+\mathrm{R}\left(\{\hat{\upsilon}_m(\mathbf{x},T)\}_{m=1}^M\right)\\&s.t.&\upsilon_m\left(\mathbf{x},T\right)=\sum_{p=1}^{P_m}\mu_{p}^{(m)}(\mathbf{x})\psi_p^{(m)}(T)\\&&\left\{\psi_p^{(m)}(T)\right\}_{m,p=1}^{M,P_m}\subset \mathrm{span}\left\{ e^{-(t-t_0)/T}u(t-t_0):t_0,T\in\mathbb{R}^+\right\}\end{matrix}$$where $$$\mathbf{x}$$$, $$$T$$$, $$$f$$$, are the spatial, temporal, and spectral coordinates, $$$\mathbf{d}$$$ is the $$$\mathcal{D}_{1,i/r}$$$ data, $$$\{\hat{\phi}_m\left(f\right)\}_{m=1}^{M}$$$ is the estimate of spectral subspace obtained from $$$\mathcal{D}_{1,b/r}$$$, $$$\mathcal{F}$$$ is the encoding and $$$B_0$$$ field inhomogeneity operator, $$$r(\mathbf{x})$$$ is a reference/support function determined from proton reference scans, $$$\left\{\psi_p^{(m)}(T)\right\}_{m,p=1}^{M,P_m}$$$ are the temporal basis functions, $$$\left\{\mu_{p}^{(m)}(\mathbf{x})\right\}_{m,p=1}^{M,P_m}$$$ are the spatial coefficients, $$$u(t)$$$ is the unit step function, and $$$\mathrm{R}\left(\cdot\right)$$$ is a regularization functional imposing a spatial smoothness prior. The model orders $$$M$$$ and $$$\{P_m\}_{m=1}^M$$$ were determined from an SVD-based analysis of the data, and given $$$\{\hat{\upsilon}_m(\mathbf{x},T)\}_{m=1}^M$$$, the image was computed as $$$\rho(\mathbf{x},T,f)=r(\mathbf{x})\sum_{m=1}^M \hat{\upsilon}_{m}\left(\mathbf{x},T\right) \hat{\phi}_m\left(f\right)$$$. The constraint on $$$\left\{\psi_p^{(m)}(T)\right\}_{m,p=1}^{M,P_m}$$$ (based on the biology of ischemia-reperfusion^1-3) replaces the temporal smoothness regularization in our previous work, and combined with $$$r(\mathbf{x})$$$, enables us to reconstruct high SNR spatial coefficients without over smoothing.

Results

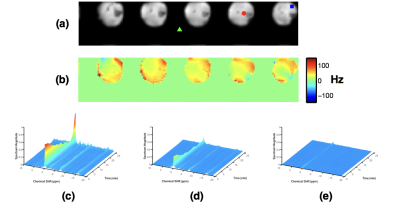
Figure 2 shows the proton reference images and some representative spectra from the reconstructions. Movies of the PCr peak integrals from the three reconstructions are shown in Fig. 3. Each reconstruction shows a gradual decrease in the peak integrals during ischemia, followed by rapid recovery during reperfusion, in good agreement with literature^1-3.

Conclusions

Acknowledgements

References

1. S. Morikawa, C. Kido, and T. Inubushi, Observation of rat hind limb skeletal muscle during arterial occlusion and reperfusion by 31P MRS and 1H MRI. Magn. Reson. Imag. 1991; 9:269-274.

2. S. Morikawa, T. Inubushi, and K. Kito, Heterogeneous metabolic changes in the calf muscle of the rat during ischemia-reperfusion: in vivo analysis by 31P nuclear magnetic resonance chemical shift imaging and 1H magnetic resonance imaging. Cardiovasc. Surg. 1993; 1:337-342.

3. Y. Liu, X. Mei, J. Li, N. Lai, and X. Yu, Mitochondrial function assessed by 31P MRS and BOLD MRI in non-obese type 2 diabetic rats. Physiol. Rep. 2016; 4(15): 12890.

4. S. C. Forbes, J. M. Slade, R. M. Francis, and R. A. Meyer, Comparison of oxidative capacity among leg muscles in humans using gated 31P 2-D chemical shift imaging. NMR Biomed. 2009; 22:1063-1071.

5. R. L. Greenman, X. Wang, and H. A. Smithline, Simultaneous acquisition of phosphocreatine and inorganic phosphate images for Pi:PCr ratio mapping using a RARE sequence with chemically selective interleaving. Magn. Reson. Imag. 2011; 29:1138-1144.

6. R. Brown, O. Khegai, and P. Parasoglou, Magnetic resonance imaging of phosphocreatine and determination of BOLD kinetics in lower extremity muscles using a dual-frequency coil array. Sci. Rep. 2016; 6:30568.

7. A. I. Schmid, M. Meyerspeer, S. D. Robinson, et al., Dynamic PCr and pH imaging of human calf muscles during exercise and recovery using 31P gradient-echo MRI at 7 Tesla. Magn. Reson. Med. 2016; 75:2324-2331.

8. L. Valkovič, M. Chmelík, M. Meyerspeer, et al., Dynamic 31P–MRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7 T. NMR Biomed. 2016; 29:1825-1834.

9. C. Ma, B. Clifford, Y. Liu, et al., High-resolution dynamic 31P-MRSI using a low-rank tensor model. Magn. Reson. Med. 2017; 78:419-428.

10. J. He, Q. Liu, A. G. Christodoulou, et al., Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors. Magn. Reson. Med. 2016; 35(9):2119-2129.

11. F. Lam, C. Ma, B. Clifford, C. L. Johnson, and Z.-P. Liang, High-resolution 1H-MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn. Reson. Med. 2016; 76(4):1059 — 1070.