0889
Towards new modalities for probing the microstructure at very high b-values1Laboratory of Condensed Matter Physics, CNRS, Palaiseau, France
Synopsis
Modern clinical and animal scanners offer versatile options for diffusion MRI, including very high b-values, at which the conventional perturbative description and related model are not applicable. We demonstrate this failure for any nontrivial domain with a boundary, regardless its shape and permeability. Since the magnetization is localized near boundaries, the signal becomes more sensitive to the microstructure. Even the signal from the extracellular diffusion is shown to be non-Gaussian at high b-values. These non-Gaussian features offer new imaging modalities at ordinary gradients accessible on most MRI scanners but, if unnoticed, they may result in misleading biomedical interpretations.
Introduction
Modern clinical and animal MRI scanners offer versatile options for diffusion MRI, including very high b-values. For instance, the b-values as high as 300 000 s/mm2 have been used for in vivo rat brain imaging1, in contrast to a conventional range up to 1 000 s/mm2. At such high b-values, perturbative descriptions and related bi-exponential, kurtosis, Kärger, and similar models may not be applicable. Their failure and the emergence of the so-called localization regime were predicted in 1990s for one-dimensional domains2 and higher-dimensional bounded domains3. However, these important works remain underappreciated even nowadays, partly because isolated impermeable compartments are not representative for biological tissues. We summarize recent mathematical advances that extend the range of applicability of the localization regime and open new modalities for probing the microstructure at very high b-values. We also show that the Gaussian paradigm generically fails at high gradients.Method
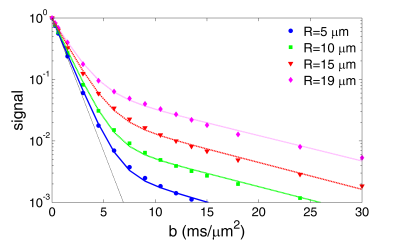
We investigated the Bloch-Torrey (BT) operator, $$$A = \nabla^2 - ix_1/\ell^3$$$, where $$$\nabla^2$$$ is the Laplace operator describing diffusion, $$$x_1$$$ is the coordinate along the gradient direction, and the gradient amplitude $$$G$$$ is represented by the gradient length $$$\ell = (\gamma G/D)^{-1/3}$$$ ($$$\gamma$$$ being the gyromagnetic ratio and $$$D$$$ the intrinsic diffusion coefficient). The BT operator governs the evolution of the transverse magnetization of the nuclei under a constant magnetic field gradient $$$\vec G$$$. We studied this operator both analytically (via spectral theory and semi-classical asymptotic analysis) and numerically (via the matrix formalism4,5 and a finite element method6). In particular, we computed the signal from water molecules diffusing in the exterior space of an array of cylindrical obstacles (Fig. 1).Results
We summarize our recent results. For one-dimensional domains with permeable boundaries (e.g., a stack of parallel permeable membranes), we computed exactly the Green function of the BT operator whose poles determine the eigenvalues of the operator7,8. In particular, the impact of permeability onto the signal was studied in detail, showing a transition from the localization regime to the Gaussian free diffusion signal. The semi-classical asymptotic analysis of the eigenmodes of the BT operator was developed for planar domains with smooth boundaries9. When the domain is much larger than the gradient length $$$\ell$$$, the eigenmodes are localized near the boundary, resulting in an “abnormal” $$$\ln(S)\propto b^{1/3}$$$ behavior at large $$$b$$$ (note that $$$b\propto \ell^{-6}$$$). We quantified the respective effects of boundary curvature, surface relaxation and permeation onto the eigenvalues and thus the signal at high gradients (see also Refs10,11).Discussion
The failure of the Gaussian paradigm and related models at high b-values originates from the non-self-adjointness of the Bloch-Torrey operator. Our mathematical analysis has revealed that the localization regime generically emerges at high (non-narrow) gradients in any nontrivial domain with a boundary, regardless whether it is bounded or not, permeable or not. Since the transverse magnetization is localized near microscopic boundaries (of cells and cellular organelles), the signal can reveal their microstructure (e.g., effective sizes and mutual arrangement) and become very sensitive to the permeability. Even the signal from water molecules diffusing in the extracellular space (an unbounded domain) exhibits the characteristic $$$\ln(S)\propto b^{1/3}$$$ behavior at large $$$b$$$ (Fig. 2), in contrast to usual Gaussian assumptions. We emphasize that the localization regime and its features are accessible at ordinary, routinely used experimental conditions on clinical and animal MRI scanners. For instance, setting $$$G = 40$$$ mT/m for a clinical scanner and $$$D = 3\cdot 10^{-9}$$$ m2/s for water molecules, one gets $$$\ell \approx 6.5 \mu$$$m so that the $$$b^{1/3}$$$ behavior is expected for cells much larger than $$$\ell$$$ (e.g., muscle or plant cells). The gradient length $$$\ell$$$ can be reduced to $$$2 \mu$$$m in animal scanners with gradients up to 1 T/m. If the emergence of the localization regime remains unnoticed, deviations from the straight line of $$$\ln(S)$$$ at high b-values could be wrongly interpreted. For instance, the application of the bi-exponential model to the curves shown in Fig. 2 yields an excellent fit but results in a strongly misleading interpretation of a model tissue in Fig. 1 in terms of intracellular and extracellular compartments with slowly and rapidly diffusing molecules, whereas only the extracellular compartment is present (see also Ref.12).Conclusion
The localization of the transverse magnetization near microscopic boundaries offer new modalities for probing the microstructure by diffusion MRI at very high b-values that complement conventional tools4,13,14. While the advantages of the localization regime are not yet fully exploitable in biological samples due to signal-to-noise limitations, a non-perturbative theory of signal formation is urged to predict, quantify and eliminate potential artifacts in clinical dMRI due to the localization regime.Acknowledgements
We acknowledge the support under Grant No. ANR-13-JSV5-0006-01 of the French National Research Agency. We also acknowledge INRIA for providing a private copy of the simulation code, developed by Jing-Rebecca Li and Dang Van Nguyen of Equipe DEFI, INRIA-Saclay.References
1. Pfeuffer J, Provencher S, Gruetter R. Water diffusion in rat brain in vivo as detected at very large b values is multicompartmental. Magn. Reson. Mat. Phys. Biol. Med. 1999;8:98-108.
2. Stoller SD, Happer W, and Dyson FJ. Transverse spin relaxation in inhomogeneous magnetic fields. Phys. Rev. A 1991;44:7459.
3. de Swiet TM and Sen PN. Decay of nuclear magnetization by bounded diffusion in a constant field gradient. J. Chem. Phys. 1994;100:5597.
4. Grebenkov DS. NMR Survey of Reflected Brownian Motion. Rev. Mod. Phys. 2007;79:1077.
5. Grebenkov DS. Laplacian Eigenfunctions in NMR I. A Numerical Tool. Conc. Magn. Reson. 2008;32A:277-301.
6. Nguyen DV, Li J-R, Grebenkov DS, Le Bihan D. A finite elements method to solve the Bloch-Torrey equation applied to diffusion magnetic resonance imaging. J. Comput. Phys. 2014;263:283-302.
7. Grebenkov DS. Exploring diffusion across permeable barriers at high gradients. II. Localization regime. J. Magn. Reson. 2014;248:164-176.
8. Grebenkov DS, Helffer B, Henry R. The complex Airy operator on the line with a semi-permeable barrier. SIAM J. Math. Anal. 2017;49:1844.
9. Grebenkov DS, Helffer B. On spectral properties of the Bloch-Torrey operator in two dimensions. SIAM J. Math. Anal. (in press); ArXiv 1608.01925v1 (2016).
10. Almog Y, Grebenkov DS, Helffer B. On a Schrödinger operator with a purely imaginary potential in the semiclassical limit (submitted); ArXiv 1703.07733 (2017).
11. Almog Y, Grebenkov DS, Helffer B. Spectral semi-classical analysis of a complex Schrödinger operator in exterior domains (submitted); ArXiv 1708.02926 (2017).
12. Grebenkov DS. Use, Misuse and Abuse of Apparent Diffusion Coefficients. Conc. Magn. Reson. 2010;A36:24-35.
13. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc. Nat. Acad. Sci. USA 2014;111:5088-5093.
14. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. 2017;30:e3602.
15. Grebenkov DS. Diffusion MRI/NMR at high gradients: challenges and perspectives. Micro. Meso. Mater. (in press)
Figures