0887
Spectral anisotropy in multidimensional diffusion encoding1Danish Research Centre for Magnetic Resonance, Copenhagen University Hospital Hvidovre, Hvidovre, Denmark, 2Clinical Sciences Lund, Radiology, Lund University, Lund, Sweden, 3Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 4Department of Chemistry, Lund University, Lund, Sweden, 5Random Walk Imaging AB, Lund, Sweden
Synopsis
To account for time-dependent diffusion in multidimensional diffusion encoding (MDE), the relevant temporal characteristics of encoding waveforms need to be identified and controlled. Based on the frequency domain analysis, we suggest a framework for analyzing the spectral content in MDE, which is useful to experimentally disentangle the effects of time-dependent diffusion. We introduce a novel concept of spectral anisotropy and demonstrate how differentiated temporal characteristics along orthogonal encoding axes may be used to isolate time-dependent diffusion in anisotropic domains, which is not possible with existing approaches without a priori model assumption.
Introduction
The need for increased specificity of diffusion MRI has lead to an upsurge of interest in non-conventional encoding waveforms. Multidimensional diffusion encoding (MDE), associated with acronyms like DDE, TDE and QTI, can unveil microscopic anisotropy on a sub-voxel level1–3. Further morphological characterization can be achieved by probing time-dependent non-Gaussian diffusion4. Understanding how MDE waveforms encode time-dependent diffusion is thus necessary. The frequency domain analysis of MDE waveforms allows identifying novel encoding dimensions capable of disentangling time-dependent diffusion effects. As we have demonstrated, spectral tuning needs to be considered to ensure unbiased microstructural assessment with MDE5. In addition, the spectrally modulated MDE allows ordering structures according to their anisotropy and e.g. size. Since the dephasing trajectories are in general three dimensional in MDE, characterization of their spectral content is non-trivial. Here we present a theoretical extension to our previous work, suggesting a framework for analyzing the spectral content in MDE5,6. Spectral moments might be used in designing spectrally tuned MDE waveforms. We introduce the concept of spectral anisotropy and demonstrate how it may provide a novel encoding dimension to independently probe time-dependent diffusion in isotropic and anisotropic morphologies.Theory
A convenient analysis of time-dependent diffusion and general encoding waveforms is provided in frequency domain7,8. Considering only the second cumulant in the signal expansion, $$$ E = e^{-\beta}$$$, the attenuation is given by $$$ \beta = \int_{-\infty}^{\infty} F_{i}(\omega)D_{ij}(\omega)F^*_{j}(\omega) \, d\omega $$$. We are adopting Einstein’s summation convention over the repeated indices $$$i, j = 1,2,3$$$. Here $$$F_{i}(\omega)$$$ are the spectra of the dephasing waveforms $$$F_i(t) = \gamma \int_{-\infty}^{\infty} g_{i}(t) dt $$$, where $$$g(t)$$$ is the effective gradient. The $$$D_{ij}(\omega) $$$ are given by rotations of the eigenmodes $$$\lambda_{i}(\omega) $$$. With the low frequency expansion7, $$$\lambda_k (\omega) = \sum_{0}^{\infty} \frac{1}{n!} \lambda_k^{(n)}(0)\,\omega^n $$$, the attenuation is given by the spectral moments $$$ M_{ij}^{(n)} = \int_{-\infty}^{\infty} F_{i}(\omega)F^*_{j}(\omega) \,\omega^n \, d\omega$$$. The moments $$$ M_{ij}^{(n)} $$$ thus provide a meaningful extension to characterize MDE waveforms and their spectral content. In terms of the spectral moments, we have $$$ B_{ij}=M_{ij}^{(0)}$$$, while the sensitivity to confinement size is provided by a dephasing moment tensor $$$ M_{ij}^{(2)} $$$, if restricted diffusion is considered7,9. The mean spectral content of MDE schemes is given by the trace of $$$m_{ij}^{(2)} = \int_{-\infty}^{\infty} \tilde{F}_{i}(\omega)\tilde{F}^*_{j}(\omega) \, \omega^2 d\omega$$$, where $$$\tilde{F}_{i}(\omega)= F_{i}(\omega)/q_{i}$$$ and $$$q_{i}$$$ is the dephasing magnitude. Spectral tuning of different MDE schemes could thus be achieved by matching the traces, $$$m_{ii}^{(2)} $$$. The fractional anisotropy of $$$m_{ij}^{(2)}$$$ provides a measure of spectral anisotropy (SA). Consider for example isotropic diffusion encoding with $$$B_{ij}=b\delta_{ij}$$$ and non-zero SA. In the presence of time-dependent diffusion, the attenuation is still expected to be rotationally invariant for compartments with isotropic diffusion, but no longer for compartments with anisotropic time-dependent diffusion, e.g. in cylinders or ellipsoids.Methods
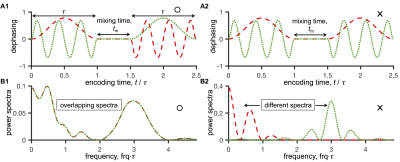
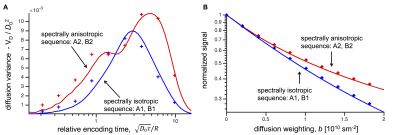
Calculations were performed using in-plane spectrally isotropic (Fig. 1A1) and anisotropic (Fig. 1A2) planar dephasing waveforms applied along two orthogonal directions. Powder averaging in the calculation was applied over 1000 directions constructed from bipolar electrostatic repulsion10. The diffusion spectrum for restricted diffusion in an axially symmetric ellipsoidal pore was approximated using $$$D(\omega)$$$ for spherical geometry with radii of 1 µm along two axes and 5 µm along one axis. The intrinsic diffusivity, $$$D_0$$$ = 10-9 m2/s was used. The encoding time $$$t_e = 2\tau + t_m$$$ was logarithmically spaced in the range 0.05-625 ms. The mixing time was adjusted to $$$t_m = 0.2t_e$$$. In addition, Monte Carlo simulations where performed with the same geometry and intrinsic diffusivity using 5·105 walkers and time-steps. Powder averaging in the simulation was performed with the ellipsoid's symmetry axis rotated along 24 directions10 with 10 linearly spaced diffusion weighting steps in the range $$$b$$$ = 0-18·109 s/m2.Results and conclusion
Effects of time-dependent diffusion in general MDE experiments can be analyzed in the frequency domain. The dephasing moment tensor provides additional characterization of encoding waveforms in terms of their spectral content. While the B tensor provides sensitivity to the long-time or Gaussian diffusivity, the dephasing moment tensor provides sensitivity to time-dependent diffusion. While varying anisotropy of the B tensor gives contrast specific to the long-time diffusion anisotropy, varying spectral anisotropy yields contrast specific to time-dependent diffusion anisotropy. In our example with planar diffusion encoding, the spectral anisotropy can be varied independently from a constant mean spectral content. The resulting signal attenuation difference carries highly specific information, isolating time-dependent diffusion in anisotropic domains.Acknowledgements
This work is supported by the Danish Council for Independent Research (4093-00280A and 4093-00280B), Vinnova, VINNMER Marie Curie Industry Outgoing (2013-04350) and the Swedish Foundation for Strategic Research (AM13-0090) and the Swedish Research Council (2014-3910).References
1. Topgaard D. Multidimensional diffusion MRI. J Magn Reson. 2016;275:98-113.
2. Shemesh N, Jespersen SN, Alexander DC, et al. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med. 2016;75(1):82-87.
3. Mitra PP. Multipule wave vector extension of the NMR pulsed gradient spin echo diffusion measurement. Phys Rev B. 1995;51(21):15074-15078.
4. Woessner D. N.M.R. spin-echo self-diffusion measurements on fluids undergoing restricted diffusion. J Phys Chem. 1963;67:1365-1367.
5. Lundell H, Nilsson M, Dyrby TB, et al. Microscopic anisotropy with spectrally modulated q- space trajectory encoding. Proc Intl Soc Mag Reson Med. 2017;25:1086.
6. Nilsson M, Lasic S, Topgaard D, Westin CF. Estimating the axon diameter from intra-axonal water di ff usion with arbitrary gradient waveforms: Resolution limit in parallel and dispersed fi bers. 2(3):3-7.
7. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Phys B. 1993;183:343-350.
8. Stepišnik J. Analysis of NMR self-diffusion measurements by a density matrix calculation. Phys B+C. 1981;104(3):350-364.
9. Nilsson M, Lasič S, Drobnjak I, Topgaard D, Westin CF. Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR Biomed. 2017;(August 2016):e3711. doi:10.1002/nbm.3711.
10. Bak M, Nielsen N. REPULSION, A novel approach to efficient powder averaging in solid-state NMR. J Magn Reson. 1997;125:132-139.
Figures