0886
Implications of nongaussian diffusion on the interpretation of multidimensional diffusion measurements1CFIN/MINDLab, Aarhus University, Aarhus C, Denmark, 2Dep. Physics and Astronomy, Aarhus University, Aarhus C, Denmark, 3Champalimaud Neuroscience Programme, Champalimaud Centre for the Unknown, Lisbon, Portugal, 4Center for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom
Synopsis
Multidimensional diffusion weighting, such as magic angle spinning of the q-vector (q-MAS), relies on the assumption of multiple Gaussian compartments (MGC). Then the kurtosis measured with q-MAS can be fully ascribed to ensemble variance of isotropic diffusivity. However, in compartments with nongaussian diffusion, anisotropic time dependence of the diffusion tensor imparts orientation dependence on the q-MAS measured mean diffusivity, which in the presence of orientation dispersion leads to additional contributions to kurtosis. Yet another contribution arises from intracompartmental kurtosis. Using simulations and experiments we demonstrate that q-MAS derived diffusion kurtosis conflates variance in isotropic diffusivity with dispersion and intracompartmental kurtosis.
Introduction
Currently, generalizations of the classical Stejskal-Tanner sequence1 for diffusion weighting are being investigated as a means to characterize microstructure or constrain modeling2-4. Multidimensional diffusion weighting4,5, which employs prolonged gradient trajectories, has been proposed to separate diffusion heterogeneity into sources stemming from orientational and isotropic diffusion variance5-9. This ability crucially depends on the assumption of multiple Gaussian compartments (MGC), but the consequences of violating MGC have not been considered in detail10. Here we show using analytical calculations, simulations, and experiments, that intracompartmental diffusion time dependence and kurtosis confound the interpretation of an isotropic diffusion weighting sequence, magic angle spinning of the q-vector (q-MAS)11,12.Methods
For the simulations, we take intrinsic diffusivity $$${{D}_{0}}=1$$$µm2/ms and use the exact solution in a rectangular box, and Monte Carlo simulations ($$${{10}^{7}}$$$particles) for regularly spaced barriers with permeability $$$\kappa =0.02$$$µm/ms in 1D, to compute the signal from the q-MAS waveform in 12. Animal experiments were preapproved by the local ethics committee and complied with local and EU laws. Fixed cervical rat spinal cord was imaged on a 16.4T Bruker Aeon Ascend magnet with gradients capable of up to 3000 mT/m. A , where a spin-echo EPI sequence was modified for q-MAS12 with a duration of τ=15 ms and separation of 1.15 ms. Imaging parameters were: bandwidth 500kHz, 2-shots, matrix size 90x54 with a partial Fourier factor of 1.2, in-plane resolution 75µm by 75µm, slice thickness 1.8mm, 4 averages, and TE/TR 40.5ms/6s. The sequence was repeated for 15 b-values from 0 to 1.5ms/µm2 and 12 different orientations. Additionally, time-dependent intra-and extra-axonal diffusivities in fixed porcine spinal cord measured with a Stejskal-Tanner sequence were obtained from 13 (‘+’ branch).Results
Under the MGC assumption, the diffusion kurtosis $$${{K}_{I}}$$$ associated with q-MAS11 can be related7 to the corresponding mean (or isotropic) diffusivity $$${{D}_{I}}$$$ and the variance $$${{V}_{I}}$$$ of isotropic diffusivities, $$${{K}_{I}}=3{{V}_{I}}/D_{I}^2$$$. However, in compartments with nongaussian diffusion, anisotropic time-dependence of the diffusion tensor imparts orientation dependence on the isotropic diffusivity measured with q-MAS, which in the presence of orientation dispersion leads to additional contributions to the variance. Further, intracompartmental diffusion kurtosis is another source of kurtosis beyond isotropic diffusion variance. These additional contributions $$$\delta K_{I}^{(1)}$$$ and $$$\delta K_{I}^{(2)}$$$ are:
(i) For identical axially symmetric microdomains with orientations $$$\mathbf{\hat{u}}$$$ and diffusivities $$${{D}_{\parallel }}(t)$$$ and $$${{D}_{\bot }}(t)$$$, apparent isotropic diffusivity is $${{\tilde{D}}_{\text{I}}}={{\delta }_{ij}}B_{ij}^{\bot }+{{\langle {{u}_{i}}{{u}_{j}}\rangle }_{{\mathbf{\hat{u}}}}}B_{ij}^{\Delta }=\text{Tr}({{\text{B}}^{\bot }})+{{\langle {{\mathbf{\hat{u}}}^{\text{T}}}{{\text{B}}^{\Delta }}\mathbf{\hat{u}}\rangle }_{{\mathbf{\hat{u}}}}},$$ where $$${{\langle \cdot \rangle }_{{\mathbf{\hat{u}}}}}$$$ denotes an average over the orientations $$$\mathbf{\hat{u}}$$$ of the microdomains, $$B_{ij}^{\bot }=({{\gamma }^2}/2b)\int_{0}^{T}{d}{{t}_{1}}\int_{0}^{T}{d}{{t}_2}{{G}_{i}}({{t}_{1}}){{G}_{j}}({{t}_2}){{D}_{\bot }}(|{{t}_{1}}-{{t}_2}|))|{{t}_{1}}-{{t}_2}|$$
$$B_{ij}^{\Delta }=({{\gamma }^2}/2b)\int_{0}^{T}{d}{{t}_{1}}\int_{0}^{T}{d}{{t}_2}{{G}_{i}}({{t}_{1}}){{G}_{j}}({{t}_2})\left( {{D}_{\parallel }}(|{{t}_{1}}-{{t}_2}|)-{{D}_{\bot }}(|{{t}_{1}}-{{t}_2}|) \right)|{{t}_{1}}-{{t}_2}|,$$ and $$$\mathbf{G}$$$ is the diffusion gradient with associated b-value $$$b$$$.
(ii) With an intracompartmental diffusivity $$$\tilde{D}_{I}^{p}$$$ and kurtosis $$$K_{I}^{p}$$$ in pore $$$p$$$, this additional contribution becomes $$\delta K_{I}^{(2)}={{\langle {{(\tilde{D}_{I}^{p})}^2}K_{I}^{p}\rangle }_{p}}/\tilde{D}_{I}^2$$ where $$${{\langle \cdot \rangle }_{p}}$$$ denotes an average over the pore population. Thus, q-MAS derived diffusion kurtosis conflates variance in isotropic diffusivity with dispersion and intracompartmental kurtosis.
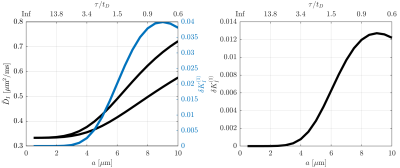
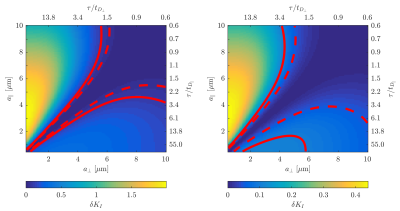
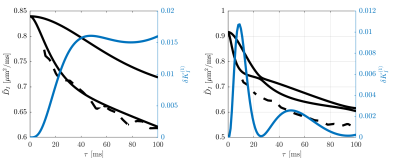
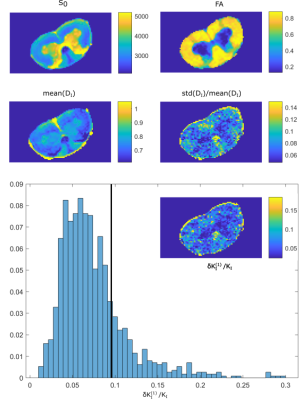
Figure 1 illustrates that $$${{\tilde{D}}_{\text{I}}}$$$ depends on the orientation of a rectangular box as function of the side length $$$a$$$, with a variability of up to varying up to more than 20% of the mean. The corresponding maximum contribution $$$\delta K_{I}^{(1)}$$$ (blue) is negligible for $$$a<5$$$µm but reaches 0.04 for larger pores. A powder average limits $$$\delta K_{I}^{(1)}<0.012$$$. Figure 2 shows $$$\delta K_{I}^{(1)}$$$ for other dimensions, and the red lines indicate regions for which where $$$\delta K_{I}^{(1)}$$$ is less than 0.01 (solid) and 0.05 (dashed). Figure 3 illustrates directional variability in pig spinal cord and compares to $$${{\tilde{D}}_{\text{I}}}$$$ computed from $$${{D}_{\parallel }}(t)$$$ and $$$D_\bot(t)$$$ obtained in 13. Figure 4 evaluates the directional dependence of $$${{D}_{I}}$$$ measured in rat spinal cord, and estimates $$$\delta K_{I}^{(1)}$$$. Finally, figure 5 illustrates the importance of intracompartmental kurtosis $$$\delta K_{I}^{(2)}$$$ for the 4 model systems.
Discussion
Interpretation of multidimensional diffusion sequences hinges on the MGC assumption. We demonstrated that violation of MGC prevents separation of orientational and isotropic heterogeneity with q-MAS, as anisotropic time-dependence and intracompartmental kurtosis led to sizable relative contributions to $$${{K}_{I}}$$$: for comparison, reported values5,8 are $$${{K}_{I}}\approx 0.3-0.6$$$. This was experimentally confirmed by a significant dependence on gradient frame orientation for q-MAS in fixed spinal cord. We note that double diffusion encoding2,3 also provides the population variance of diffusion tensors without the MGC assumption14,15, and that other multidimensional diffusion sequences that are less sensitive with less sensitivity to nongaussianity could be designed.Conclusion
Experimentally observed deviations from the MGC assumption call for caution when interpreting multidimensional diffusion weighting. Specifically, additional important contributions to variance in diffusivity arise from dispersion of compartments with anisotropic diffusion time dependence, and intracompartmental diffusion kurtosis.Acknowledgements
SNJ is supported by the Danish National Research Foundation (CFIN), and The Danish Ministry of Science, Innovation, and Education (MINDLab). Funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Starting Grant, agreement No. 679058) supports NS, and funding from EPSRC grant number M507970 supports AI. We thank Dr. Daniel Nunes for tissue extraction.References
1. Stejskal, E.O. and J.E. Tanner, Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. The Journal of Chemical Physics, 1965. 42(1): p. 288-292. 2. Cheng, Y. and D.G. Cory, Multiple scattering by NMR. J. Am. Chem. Soc., 1999. 121(34): p. 7935-7936. 3. Shemesh, N., et al., Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med, 2016. 75(1): p. 82-7. 4. Topgaard, D., Multidimensional diffusion MRI. J Magn Reson, 2017. 275: p. 98-113. 5. Westin, C.F., et al., Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 2016. 135: p. 345-62. 6. Lampinen, B., et al., Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. Neuroimage, 2017. 147: p. 517-531. 7. Lasic, S., et al., Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2014. 2. 8. Szczepankiewicz, F., et al., The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage, 2016. 142: p. 522-532. 9. Szczepankiewicz, F., et al., Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage, 2015. 104: p. 241-52. 10. Ianus, A., et al. Metrics of microscopic anisotropy: a comparison study. in Proc. Int. Soc. Magn. Reson. Med. 2016. Singapore, Singapore. 11. Eriksson, S., S. Lasic, and D. Topgaard, Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. J Magn Reson, 2013. 226: p. 13-8. 12. Nilsson, M., et al., Liquid crystal phantom for validation of microscopic diffusion anisotropy measurements on clinical MRI systems. Magn Reson Med, 2017. 13. Jespersen, S.N., et al., Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage, 2017. 14. Jespersen, S.N., et al., Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR Biomed, 2013. 26(12): p. 1647-62. 15. Jespersen, S.N., Equivalence of double and single wave vector diffusion contrast at low diffusion weighting. NMR Biomed, 2012. 25(6): p. 813-8.Figures