0884
LEMONADE(t): Exact relation of time-dependent diffusion signal moments to neuronal microstructure1Center for Biomedical Imaging, New York University, New York, NY, United States
Synopsis
The purpose of this work is to solve the two complementary problems: (i) Estimate the time-dependent (non-Gaussian) signatures of intra- and extra-neurite tissue compartments separately, irrespective of neurite orientational dispersion; and (ii) cure the notorious degeneracy in parameter estimation of multi-compartment models. We derive exact relations between time-dependent 2nd- and 4th-order signal moments, and all relevant time-dependent diffusion parameters in the intra- and extra-neurite space. Remarkably, the temporal dimension lifts the degeneracy in parameter estimation: The relations are formally invertible, multiple "branches" of solutions do not appear, and time-dependent DKI is enough to estimate all parameters. Precision, though, remains a challenge.
Introduction
So far, most neuronal-microstructure models estimate Gaussian compartment parameters (cf. e.g. review1), yet microstructural length-scale can only be obtained from non-Gaussian features in each compartment. Unfortunately, the general functional form of diffusion propagator for all $$$q$$$ and $$$t$$$ is not known. Here we use asymptotic relations between long-time approach of tortuosity limit2-4, and time-dependent kurtosis in each compartment, to establish a closed-form tissue model for low diffusion-weighting. Parameter estimation becomes formally exactly solvable at the level of 2nd- and 4th-order cumulants (DKI).
Theory
The $$$t$$$-dependent extension of the Standard Model is outlined in Fig.1. The crucial relations, that allow us to "close" the problem up to order $$$b^2$$$, by relating the time-dependence of diffusion and kurtosis in each direction/compartment, are2-4:
$$D_a(t)=D_{a,\infty}+\frac{c_a}{\sqrt{t}}\,,\quad\,K_a(t)=\frac{2c_a}{D_{a,\infty}}\cdot\frac{1}{\sqrt{t}}\,,\quad\quad$$
$$D_e^\parallel(t)=D_{e,\infty}^\parallel+\frac{c_e^\parallel}{\sqrt{t}}\,,\quad\,K_e^\parallel(t)=\frac{2c_e^\parallel}{D_{e,\infty}^\parallel}\cdot\frac{1}{\sqrt{t}}\,,\quad\quad$$
$$D_e^\perp(t)=D_{e,\infty}^\perp+c_e^\perp\cdot\frac{\log(t/\delta)}{t}\,,\quad\,K_e^\perp(t)=\frac{6c_e^\perp}{D_{e,\infty}^\perp}\cdot\frac{\log(t/\delta)}{t}\,.\quad\quad$$
Here $$$D_a(t)$$$ and $$$D_e^\parallel(t)$$$ account for time-dependence parallel to axons in intra- and extra-axonal space; time-dependence transverse to axons is solely determined by extra-axonal space in $$$D_e^\perp(t)$$$, due to thin axons. Time-dependence is parametrized by: $$$\delta$$$ (diffusion-gradient pulse-width) and $$$t\equiv\Delta$$$.
Tissue parameters: $$$f$$$ is intra-axonal water fraction, $$$\{D_{a,\infty}\,,\,D_{e,\infty}^\parallel\,,\,D_{e,\infty}^\perp\}$$$ are bulk (tortuosity-limit) diffusivities at $$$t\to\infty$$$, $$$\{c_a\,,\,c_e^\parallel\,,\,c_e^\perp\}$$$ are strengths of restrictions in each compartment/direction. We denote $$$x=\{f\,,\,D_{a,\infty}\,,\,D_{e,\infty}^\parallel\,,\,D_{e,\infty}^\perp\,,\,c_a\,,\,c_e^\parallel\,,\,c_e^\perp\}$$$ as an overall set of parameters to be estimated (Fig.1).
By using above time-dependence in compartmental kernels $$${\cal{K}_{\rm{in}}}$$$ and $$${\cal{K}_{\rm{ex}}}$$$ in Eq.(2), we estimate all the parameters without assuming the shape of ODF or relations between tissue parameters, Fig.1. We factorize5,6 Eq.(1),Fig.1 in the spherical harmonics basis, and relate tissue parameters $$$x$$$ to the symmetric moment tensors5 $$$M^{(l)}$$$ up to order $$$l\le{L_{\rm{max}}}=4$$$ (Eq.(3)). $$$M^{(2)}$$$ is the overall diffusion tensor, $$$M^{(4)}$$$ is the combination of kurtosis and diffusion tensor, and $$$0\le\,p_2\le1$$$ is a rotationally-invariant "nonlinear FA" of fibers.5,6
The overall philosophy of this approach follows the LEMONADE5 solution for the moments (Linearly Estimated Moments provide Orientations of Neurites And their Diffusivities Exactly); the added time-dependence of $$$M^{(2)}$$$ and $$$M^{(4)}$$$ provides extra-dimension for model fitting to break the degeneracy5-7 in parameter estimation of multi-compartment models. The work takes the promising approach of Jespersen et al.8 to its logical conclusion, using the temporal relations not just to select the branch, but to estimate all parameters simultaneously.
Methods
$$$\bf{Noise\;Propagation}$$$
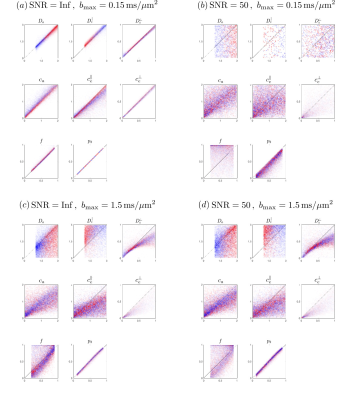
In Fig.2, to show the influence of b-value and SNR on the precision of fits to Eq.(3),Fig.1, we use a b-table with [$$$b=\{0.1,0.4,1,1.5\}$$$] ms/$$$\mu$$$m$$$^2$$$ in 64 directions, generate artificial signal based on Eq.(1) under SNR=$$$\infty$$$ and 50, calculate moments$$$\,M^{(l)}\,$$$and solve$$$\,x\,$$$ by inverting Eqs.(3),Fig.1. Then we further scale down the b-values by 10, i.e. maximal b-value=0.15 ms/$$$\mu$$$m$$$^2$$$, to test the precision (Fig.3).
$$$\bf{Phantom\,MRI}$$$
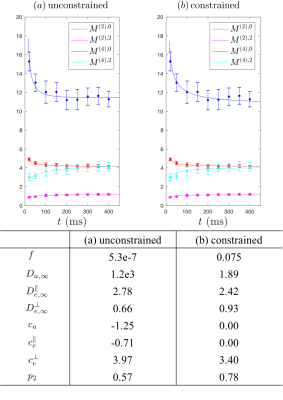
Diffusion measurements were performed on a fiber phantom3 composed of aligned Dyneema solid fibers (radius$$$\,=8.5\pm1.3\,\mu$$$m) submersed in water, with only extra-fiber space, on a 3T Siemens Prisma. 2 b=0 images and 63 DWIs with $$$b=\{0.1,0.2,0.4,1\}$$$ms/$$$\mu$$$m$$$^2$$$, $$$t=20-400\,$$$ms, $$$\delta=15\,$$$ms. TE/TR=468/12500 ms, resolution=$$$1.5\times1.5\times5$$$mm$$$^3$$$.
$$$\bf{Human\,Brain\,MRI}$$$
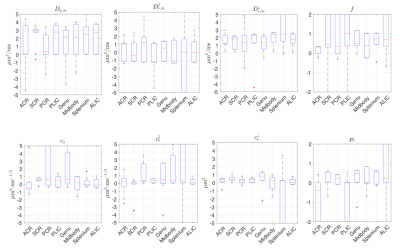
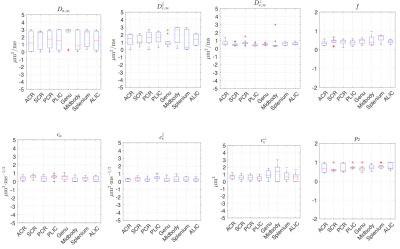
Diffusion measurements were performed on 10 healthy subjects9 (7M/3F, 23-30-yo) on a 3T Siemens Prisma. 1 b=0 image and 64 DWIs with $$$b=\{0.1,0.4,1,1.5\}$$$ms/$$$\mu$$$m$$$^2$$$, $$$t=21.2-100\,$$$ms, $$$\delta=15\,$$$ms,TE/TR=150/5000 ms, resolution=$$$(2$$$mm$$$)^3$$$. Moments are averaged over standard white matter ROIs.
For simulation, we solved Eqs.(3),Fig.1, by linear-regression up to 2nd-order time-dependent terms; these coefficients, together with $$$t$$$-independent terms, yield a linearly-solvable system for all $$$x$$$. For MRI data, to increase precision, Eqs.(3),Fig.1 were inverted by nonlinear trust-region-reflective method, with or without biological lower bound of $$$0$$$ for all parameters, and upper bounds $$$\{D_a\,,\,D_{e,\infty}^\parallel\,,\,D_{e,\infty}^\perp\}\le3\mu$$$m$$$^2$$$/ms, $$$0\leq\,p_2\leq\,1$$$.
We emphasize that our constraints are "mild": they are not used to select a "branch" within parameter space (out of degenerate/plausible fit minima), but rather for robustness.
Results
Fig.2 shows noise propagation using exact linear inversion of Eqs.(3),Fig.1. At infinite SNR and low b, Fig.2a, where cumulant expansion is unbiased, parameters are estimated nearly exactly. However, at SNR=50, Eq.(3) fails due to low contrast-to-noise. Fig.2c shows that Eq.(3) is biased in higher b-value, and yet is less vulnerable to noise. Generally, estimates of$$$\,D_{e,\infty},c_a,c_e^\parallel,c_e^\perp\,$$$have higher precision.
Fig.3a shows that Eqs.(3),Fig.1 describe the phantom data well. Unconstrained fits lead to lower precision in parameters estimations, and constrained fits in Fig.3b provide estimates consistent with previous study3. Estimates of$$$\,c_e^\perp\,$$$related to fiber diameter is consistent in both constrained and unconstrained fits.
Fig.4 shows that, in the human data of low SNR~10, unconstrained fits are highly biased. In contrast, constrained fits in Fig.5 offers parameters in a reasonable scale, although some estimated$$$\,D_{a,\infty},D_{e,\infty}^\parallel,D_{e,\infty}^\perp\,$$$hits the bounds. In Fig.5,$$$\,c_e^\perp\propto($$$outer diameter$$$)^2\,$$$,ref3, shows the well-known low-high-low trend in genu-midbody-splenium of corpus-callosum.
Discussion and Conclusions
Estimation of time-dependent compartmental parameters is in principle possible. None of the compartmental-disorder-strengths $$$c$$$ can be discarded, as they are all non-negligible. Precision remains a challenge, yet it is not a bug, but a feature of the problem: If parameters are relevant, we must include them and work on improving precision through innovative hardware/acquisitions.
Acknowledgements
We would like to thank Thorsten Feiweier for developing advanced diffusion WIP sequence, and Antonios Papaioannou for sharing human brain data. Research was supported by the National Institute of Neurological Disorders and Stroke of the National Institutes of Health under award number R01NS088040.References
[1] Novikov, D. S., Jespersen, S. N., Kiselev, V. G. & Fieremans, E. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. arXiv preprint arXiv:1612.02059 (2016).
[2] Novikov, D. S., Jensen, J.H., Helpern, J.A., Fieremans, E. Revealing mesoscopic structural universality with diffusion. PNAS, 111(14), 5088-5093 (2014)
[3] Burcaw, L.M., Fieremans, E., and Novikov, DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage 114 (2015) 18–37
[4] Fieremans, E., et al. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. NeuroImage, 129, 414-427 (2016).
[5] Novikov, D. S., Veraart, J., Jelescu, I. O. & Fieremans, E. Mapping orientational and microstructural metrics of neuronal integrity with in vivo diffusion MRI. arXiv preprint arXiv:1609.09144 (2016).
[6] Reisert, M., Kellner, E., Dhital, B., Hennig, J. & Kiselev, V. G. Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. NeuroImage 147, 964-975, (2017).
[7] Jelescu, I. O., Veraart, J., Fieremans, E. & Novikov, D. S. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. 29, 33-47, (2016).
[8] Jespersen, S.N. et al. Diffusion time dependence of microstructural parameters in fixed spinal cord. NeuroImage (2017), DOI: 10.1016/j.neuroimage.2017.08.039
[9] Papaioannou A., et al. Proc ISMRM 25, 723 (2017).
Figures
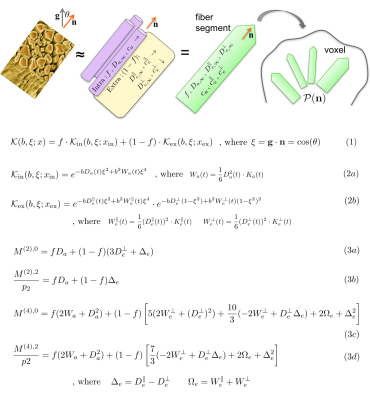
Figure 1. The dMRI signal $$$S_{\bf{g}}(b)$$$ along gradient direction $$$\bf{g}$$$, with a diffusion weighting $$$b=q^2t$$$ and diffusion time $$$t$$$, is a convolution of the anisotropic kernel $$${\cal{K}}(b,{\bf{g}}\cdot{\bf{n}})$$$ with a fiber ODF $$${\cal{P}}({\bf{n}})$$$ on a unit sphere $$$|{\bf{n}}|=1$$$, shown in Eq.(1), where $$$\xi={\bf{g}}\cdot{\bf{n}}$$$ and $$$x$$$ is a set of scalar compartmental parameters to be estimated. The overall kernel is the weighted sum of intra-axonal kernel $$${\cal{K}_{\rm{in}}}$$$ and extra-axonal kernel $$${\cal{K}_{\rm{ex}}}$$$. We derive exact relations between rotationally-invariant moments $$$M^{(2)}$$$ and $$$M^{(4)}$$$, and tissue parameters, Eq.(3). These relations appear to be exactly invertible linearly (not shown).