0883

Including diffusion frequency dependence in the extra-axonal space to improve axonal diameter mapping using trapezoidal OGSE sequences
Kevin GINSBURGER1, Fabrice POUPON2, Felix MATUSCHKE3, Jean-François MANGIN2, Markus AXER3, and Cyril POUPON1

1UNIRS, CEA/ISVFJ/Neurospin, Gif-sur-Yvette, France, 2UNATI, CEA/ISVFJ/Neurospin, Gif-sur-Yvette, France, 3INM-1 Forschungszentrum Jülich, Jülich, Germany

Synopsis

We performed Monte-Carlo simulations of the diffusion process in 3D biomimetic geometries accounting for the angular dispersion and tortuosity present in white matter. Diffusion MRI data synthesis using clinically plausible trapezoidal OGSE sequences was then performed and an extra-axonal linear-in-frequency dependence of the perpendicular diffusivity transverse to axons was observed over a wide range of axon diameter values. Simulated data was fed into an ActiveAx trapezoidal OGSE model accounting for this frequency-dependence. The estimation of axonal diameter is improved by this correction.

Introduction

Similarly to the diffusion time-dependence observed in single-diffusion-encoding sequences1,2, an oscillating gradient spin-echo (OGSE) experiment3,1 suggested that, at low frequencies (<400 Hz), the OG-measured extra-axonal diffusivity perpendicular to axons has a linear-in-frequency dependence, while current OGSE multi-compartment models usually assume Gaussian diffusion in the extra-axonal space4,5. A correction was recently proposed for cosine OGSE (cOGSE)6. Likewise, though using trapezoidal OGSE (tOGSE) to perform axonal calibration seems a promising approach7,8,9, a correction should be added to the extracellular tOGSE signal model to account for this frequency-dependence and provide reliable estimates. Thus, we performed Monte-Carlo simulations of the diffusion process in 3D biomimetic geometries accounting for the angular dispersion and tortuosity present in white matter. dMRI data synthesis using clinically plausible tOGSE sequences was then performed and an extra-axonal linear-in-frequency dependence over a wide range of axon diameter values was observed. Simulated data was fed into an ActiveAx tOGSE model accounting for this frequency-dependence. The estimation of axonal diameter is improved by this correction.

Methods

White matter is modeled as three tissue compartments. The full model for the diffusion MR signal $$$S$$$ writes (no exchange between compartments is assumed5,10,11):

$$S = (1 - \nu_{iso})( \nu_{ic}S_{ic} + ( 1 - \nu_{ic})S_{ec} ) + \nu_{iso}S_{iso}~~~~~(1)$$

where $$$S$$$ and $$$\nu$$$ are the normalized signal and associated volume fraction of a given compartment and $$$iso$$$, $$$ic$$$ and $$$ec$$$ refer to the CSF (isotropic Gaussian displacements12), intra- and extra-cellular compartments. The intra-cellular signal $$$S_{ic}$$$ from particles trapped inside a cylinder with direction n is computed using the Gaussian Phase Distribution approximation for tOGSE13. Extra-axonal diffusion is characterized by an extracellular diffusion tensor $$$D_{ec}$$$ :

$$S_{ec} = e^{b G^T D_{ec}(n,\nu_{ic})G}~~~~~(2)$$

where $$$b$$$ is the $$$b$$$-value of the diffusion sequence, $$$G$$$ represents the gradient magnitude. $$$D_{ec}$$$ is decomposed as11 :

$$D_{ec}(n,\nu_{ic}) = ( d - d_{\perp}(\nu_{ic}) )nn^T + d_{\perp}(\nu_{ic})I~~~~~(3)$$

where $$$d_{\perp}$$$ is the diffusion coefficient perpendicular to axons and $$$I$$$ the identity tensor. Similarly to cOGSE6, a frequency-dependence correction is added to $$$d_{perp}$$$ for tOGSE sequences at frequency $$$|\omega_0|$$$, accounting for the linear-in-frequency dependence of the diffusion coefficient transverse to axons1:

$$d_{\perp} = d_{\perp,\infty} + A\frac{\pi}{2}|\omega_0|~~~~~(4)$$

Theoretically, equation (4) holds only in the case of a cOGSE whose encoding spectrum approximately writes14

$$|F(\omega)|^2 = (\frac{\pi \gamma G}{\omega_0})^2[\delta(\omega+\omega_0) + \delta(\omega-\omega_0) ]~~~~(5)$$

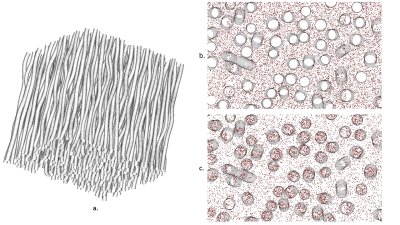
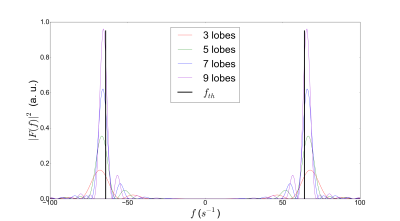
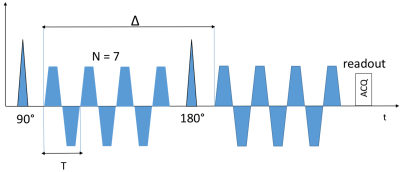
for a sufficient number of oscillations. However, it was shown that the differences between the encoding spectrum of cOGSE and tOGSE with equal frequency are minimal14. Equation (4) can thus be used with tOGSE sequences having a high selectivity around $$$\omega_0$$$. Monte-Carlo simulations were performed with the Diffusion Microscopist Simulator15 using a numerical phantom mimicking white matter structural disorder with an angular dispersion of 10 degrees (fig.1). 307 / 741 cylindroids (volume fractions of 0.25 / 0.5) were packed inside a cube subdivided into 27 voxels. Only the central voxel was considered in order to make the simulation finite-size effects negligible. Particles followed a 3D Brownian motion dynamics, elastically reflecting onto the cylindroid membranes, with a diffusivity of 2.00 .10-9 m²/s and temporal step of 1.0 µs. dMRI data synthesis was performed using a simulated tOGSE sequence depicting 7 lobes (due to its frequency selectivity, see fig.2), a refocusing pulse of 10 ms and a slew rate of 200 T/m/s(fig.3), that can effectively be tuned on recent Connectome 3T scanners equipped with 80mT/m gradient sets.


Results & Discussion

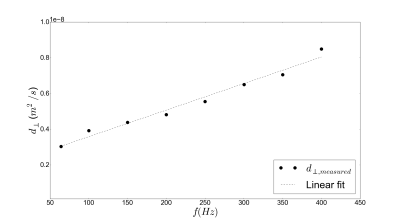
A first simulation was launched by placing 109 particles in the extracellular space with impermeable axonal membranes (mean diameter 2.00 µm, volume fraction 0.5) so that the obtained signal comes only from diffusion in the extracellular space (fig.1.b). A linear relationship between the extracellular perpendicular diffusivity and the tOGSE frequency varied on the range 64-400 Hz at constant gradient magnitude (75 mT/m) was observed (fig.4), validating our extracellular model. Diffusing particles were then placed in both intra- and extra-cellular space (fig.1.c). A 100 Hz tOGSE sequence with gradient magnitudes varied to acquire data at $$$b$$$-values from 0 to 1700 s/mm2 was used. The axonal diameter was varied from 2.00 µm to 10.00 µm, for two values of intracellular volume fraction (0.25 and 0.5). 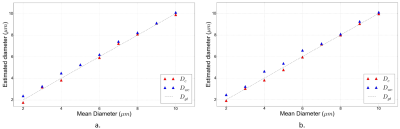Figure 5 shows a diminution of axon diameter mapping error for all diameter values when using the frequency-dependence correction. This diminution is more important at diameter values below 7.00 µm and for the biggest volume fraction of 0.5, for which the structural disorder of axonal packing is the strongest1.

Conclusion

By comparing the estimated diameter to the ground truth provided by simulation, we showed that adding a linear-in-frequency term in the extra-axonal tensor perpendicular diffusivity enables to obtain a better estimation of axonal diameter using an ActiveAx tOGSE model. Further work will consist in applying such a correction to obtain axonal diameters in vivo estimates using tOGSE sequences.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation under Grant Agreement No 720270 (Human Brain Project SGA1).

References

1. Burcaw, L. M., Fieremans, E., and Novikov, D. S. (2015). Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage 114, 18–37.

2. De Santis, S., Jones, D. K., and Roebroeck, A. (2016). Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage 130, 91–103.

3. Portnoy, S., Flint, J., Blackband, S., and Stanisz, G. (2013). Oscillating and pulsed gradient diffusion magnetic resonance microscopy over an extended b-value range: Implications for the characterization of tissue microstructure. Magnetic resonance in medicine 69, 1131–1145.

4. Drobnjak, I., Zhang, H., Ianuş, A., Kaden, E., & Alexander, D. C. (2016). PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magnetic resonance in medicine, 75(2), 688-700.

5. Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J., et al. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 52,1374–1389.

6. Ginsburger, K., Poupon, C. (2017). Frequency dependence of the extra-axonal diffusion coefficient for ogse sequences. In Proc. ESMRMB 2017, Barcelona, Spain.

7. Nilsson, M. (2016). Estimating the axon diameter from intra-axonal water diffusion with arbitrary gradient waveforms: resolution limit in parallel and dispersed fibers. In Front. Phys. Conference Abstract: New dimensions in diffusion encoding. doi: 10.3389/conf. FPHY. vol. 6.

8. Drobnjak, I., Siow, B., & Alexander, D. C. (2010). Optimizing gradient waveforms for microstructure sensitivity in diffusion-weighted MR. Journal of Magnetic Resonance, 206(1), 41-51.

9. Kakkar, L. S., Bennett, O. F., Siow, B., Richardson, S., Ianus ̧, A., Quick, T., et al. (2017). Low frequency oscillating gradient spin-echo sequences improve sensitivity to axon diameter: An experimental study in viable nerve tissue. NeuroImage.

10. Assaf, Y., Blumenfeld-Katzir, T., Yovel, Y., and Basser, P. J. (2008). Axcaliber: a method for measuring axon diameter distribution from diffusion mri. Magnetic resonance in medicine 59, 1347–1354.

11. Zhang, H., Hubbard, P. L., Parker, G. J., & Alexander, D. C. (2011). Axon diameter mapping in the presence of orientation dispersion with diffusion MRI. Neuroimage, 56(3), 1301-1315.

12. Barazany, D., Basser, P. J., and Assaf, Y. (2009). In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain 132, 1210–1220.

13. Ianus ̧, A., Siow, B., Drobnjak, I., Zhang, H., and Alexander, D. C. (2013). Gaussian phase distribution approximations for oscillating gradient spin echo diffusion mri. Journal of Magnetic Resonance 227, 25–34.

14. Van, A. T., Holdsworth, S. J., & Bammer, R. (2014). In vivo investigation of restricted diffusion in the human brain with optimized oscillating diffusion gradient encoding. Magnetic resonance in medicine, 71(1), 83-94.

15. Yeh, C.-H., Schmitt, B., Le Bihan, D., Li-Schlittgen, J.-R., Lin, C.-P., and Poupon, C. (2013). Diffusion microscopist simulator: a general Monte-Carlo simulation system for diffusion magnetic resonance imaging. PloS one 8, e76626.

Figures

Fig. 1 a. Mesh with intracellular volume fraction of 0.25 employed for simulations (only a small subset of the mesh is shown for illustration purposes). The cylindroids are rotated and deformed to mimick tortuosity and angular dispersion present in white matter. The membranes of the cylindroids are impermeable. Axonal diameter here follows a Gaussian distribution with mean 2.00 µm and variance 0.2 µm. Figure b. and c. show a cross-section of the simulation domain, with diffusing particles in red, placed only in the extracellular space (b.) or in the whole simulation domain (c.) corresponding to the two types of simulations performed.

Fig. 2 Power modulation spectra for trapezoidal OGSE gradient waveforms with the same parameters as the sequence employed in this article but for different number of half periods, showing the influence of the number of lobes on the frequency selectivity. The theoretical peak frequency is denoted as $$$f_{th}$$$. We observe that the difference between this theoretical peak and the actual frequency peak of the sequence decreases with increasing number of lobes. The actual frequency peak (not the theoretical one) is fed in our model for better precision. 7 lobes is a good compromise to have a satisfying frequency selectivity with an acceptable acquisition time.

Fig. 3 Schematic representation of the employed trapezoidal OGSE gradient waveform with zero phase and integer number of half periods (N = 7).

Fig. 4 Perpendicular diffusivity in the extracellular space measured by performing Monte-Carlo simulations with diffusing particles in the extracellular space only (axonal diameters following a Gaussian distribution with mean 2.00 µm and standard deviation 0.20 µm, angular dispersion of 10 degrees, intracellular volume fraction of 0.5 ), plotted against the frequency of the employed tOGSE sequence. A linear fit is also plotted which shows the linear dependence of diffusivity to frequency.

Fig. 5 Estimated versus ground truth diameter for various mean diameters of the phantom cylindroids. $$$D_c$$$ corresponds to diameter estimates obtained using the analytical model including the frequency dependence correction, while $$$D_{wc}$$$ refers to the estimated mean axonal diameter obtained without the use of this correction. Figure a. gives the results for a volume fraction of 0.25, figure b. for a volume fraction of 0.5. The global angular dispersion and tortuosity values are the same for all simulations (total angular dispersion of 10 degrees).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0883