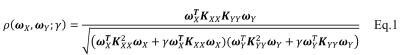Introduction

Data fusion techniques have been proposed in the recent past to leverage complementary information of multiple modalities. Many fusion studies used principal component analysis (PCA) for dimension reduction prior to associating modalities to overcome the problem of having more voxels than observations [1]. PCA, however, does not address that a large proportion of voxels might be irrelevant for a fusion analysis. In our study, we integrated sparse regularization into PCA and developed a technique to control the sparsity level. This sparse PCA (sPCA) method was then applied together with canonical correlation analysis (CCA) to fuse resting-state fMRI data and structural data acquired from normal controls (NC) and subjects with mild cognitive impairment (MCI).

Method

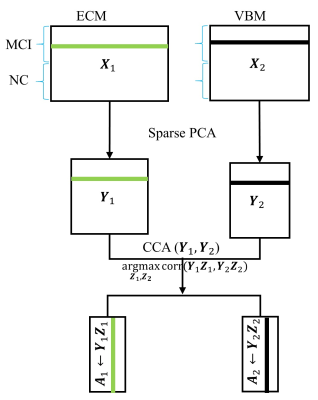
Subjects: Both structural and resting-state functional MRI data from 22 age- and gender-matched MCI subjects (F/M=10/12, age=74.72±4.02 ys, all amyloid positive) and 22 NC (F/M=12/10, age=74.61±6.02 ys) were obtained from the ADNI database (http://adni.loni.usc.edu/). Standard preprocessing steps, including slice-timing correction, realignment, coregistration, and normalization, were performed for fMRI data. Fast eigenvector centrality mapping (ECM) [2] was performed on each subject, yielding individual voxel-wise whole brain centrality maps as a measure of functional connectivity. Voxel-based morphometry (VBM) using SPM12 was applied on T1 structural data to create statistical VBM maps. sPCA+CCA: The schematic diagram of the sparse PCA+CCA fusion method is shown in Fig.1. sPCA is performed on ECM and VBM maps separately to generate a dimension-reduced data set $$$Y_r$$$. The input data to sPCA has a dimension of subjects x voxels. Since the goal of implementing sparsity is to suppress irrelevant voxels, L₁ sparsity penalty term over voxels $$$||v||_1<=c$$$ is added to the conventional PCA but not over subjects. The objective function in sPCA is formulated as Eq.1. Considering that conventional PCA has the L₂ penalty, the penalty in sPCA is the elastic penalty and thus sPCA has a unique solution even when the number of voxels is larger than the number of subjects. sPCA is solved by an alternating iteration method [3]. An imputation method is developed to select the sparsity level and the number of principal components. In detail, one tenth of elements are randomly removed from the data matrix, then sPCA is applied on the imputed matrix to optimize sparsity parameters. The number of principal components is determined by using the Akaike information criterion [4]. Then CCA is applied on $$$Y_r$$$ to maximize the canonical correlation between imaging modalities. Finally, the spatial maps corresponding to $$$A_r$$$ can be obtained as $$$C_r=A_r^+X_r$$$. Methods comparison: sPCA+CCA was compared with previously introduced fusion methods including PCA+CCA [5], parallel ICA [6] and sparse CCA (sCCA). Two sample t-tests with unequal variances were applied on each component of modulation profiles $$$A_r$$$. Receiver operating characteristic (ROC) method was performed on $$$A_r$$$ to determine group separation for each component and the area under ROC ($$$AUC$$$) was calculated.

Results

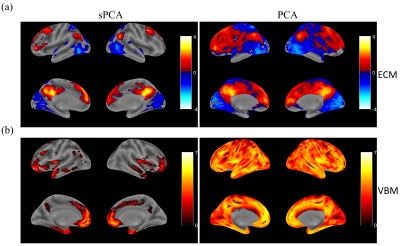
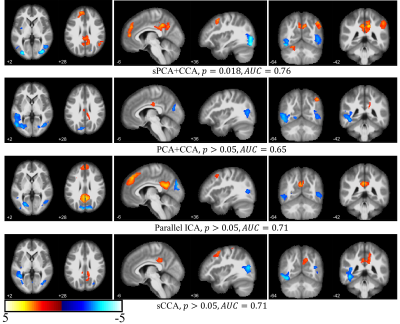
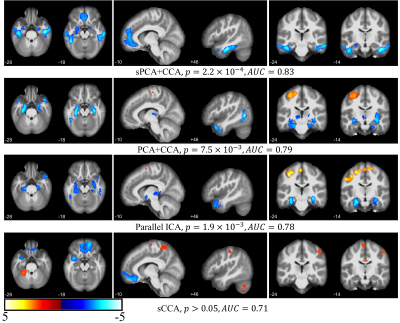
The principal components having largest variance from sPCA and PCA are shown in Fig.2. No threshold is applied for both ECM maps (Fig.2a) and VBM maps (Fig.2b). In sPCA, around 70% of voxels have been specified as zero at the optimal sparsity level. As can be seen in Fig.2, sPCA keeps high-weight voxels in the default mode network but removes most low-weight voxels. Fig.3 and Fig.4 show the most significant group-discriminant ECM and VBM z-score maps from sPCA+CCA, PCA+CCA, parallel ICA and sCCA with threshold $$$|z|>2$$$. The clusters in the spatial maps passing corrected $$$p<0.05$$$ are listed in Table1. In the ECM dataset, only the component from sPCA+CCA is significant (corrected $$$p=0.018, AUC=0.76$$$). In the VBM dataset, the component from sPCA+CCA is the most significant among these four fusion methods and there is no significant component in sCCA (sPCA+CCA: corrected $$$p=2.2 \times 10^{-4}, AUC=0.83$$$; PCA+CCA: corrected $$$p=7.5 \times 10^{-3}, AUC=0.79$$$; parallel ICA: corrected $$$p=1.9 \times 10^{-3}, AUC=0.78$$$). Overall, sPCA+CCA has the strongest statistical power in discriminating MCI from NC in terms of $$$AUC$$$.

Discussion

We have proposed a sPCA method to eliminate irrelevant voxels and developed an imputation method to control the signal sparsity level and number of principal components. Furthermore, sPCA was applied together with CCA to fuse fMRI and T1 images. Compared with three state-of-the-art fusion methods, the components obtained from sPCA+CCA in both modalities are most group-discriminative. The default mode network in ECM and hippocampus in VBM found by sPCA+CCA corroborate with other studies [7, 8].

Conclusion

sPCA is a powerful method for sparse regularization and dimensionality reduction. In addition, sPCA is completely data-driven and self-adaptive without user intervention.

Acknowledgements

The study is supported by the National Institutes of Health (grant number 1R01EB014284 and P20GM109025). Data collection and sharing for this project was funded by the ADNI (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012).