0836

Inter-slice current constrained B0 shim optimization for high order dynamic shim updating with strongly reduced eddy currents
Michael Schwerter1, Chan Hong Moon2, Hoby Hetherington2, Jullie Pan2, Lutz Tellmann1, Jörg Felder1, and N. Jon Shah1,3

1Institute of Neuroscience and Medicine, Medical Imaging Physics (INM-4), Forschungszentrum Jülich, Jülich, Germany, 2Department of Radiology, University of Pittsburgh, Pittsburgh, PA, United States, 3Faculty of Medicine, Department of Neurology, RWTH Aachen University, Aachen, Germany

Synopsis

Dynamic shim updating using spherical harmonics is an effective B0 shim technique, but known to induce eddy currents which degrades the achievable shim quality. Current DSU implementations therefore use pre-emphasis which requires additional hardware and time-consuming system calibrations. To reduce eddy current generation, we have implemented an optimization algorithm which limits the maximum inter-slice shim current change. It is based on the assumption that a smooth variation of shim currents with small current steps will substantially reduce eddy currents. Simulations and initial experiments have shown that eddy currents can be drastically reduced without significant impact on the achievable shim quality.

Introduction

Magnetic field inhomogeneities are still a severe problem for numerous MR applications motivating the need for more effective B0 shim techniques. Amongst recent approaches1,2, dynamic shim updating (DSU) using spherical harmonics (SH) has proven to yield better B0 homogeneity than static approaches3.

However, shim optimization over small volumes can result into excessive shim currents and rapid shim switching can generate eddy currents (ECs). In DSU applications these phenomena add up in the formation of potentially strong ECs and require additional hardware and time-consuming pre-emphasis implementations.

To address these issues, we implemented an algorithm that limits the inter-slice shim current changes. It is based on the assumption that for typically chosen slice thicknesses the susceptibility distribution and its associated shim profile varies smoothly. We hypothesize that the rate of change of DSU currents can be highly constrained while marginally affecting shim quality. This will reduce ECs, limit hardware requirements and may ultimately enable DSU without the need of pre-emphasis.

Methods

Measurements were performed on a 3T TRIO (Siemens) equipped with a SH shim insert driven by a power supply with ±5A output current per channel and a DSU unit enabling dynamic shimming up to full 4th and partial 5th/6th order (Resonance Research Inc.). Axial B0 fieldmaps were acquired4 with 3mm isotropic resolution covering a volume of 192x192x99mm3.

DSU currents are calculated by minimizing ||Ak·xk–bk||2, where A is the SH system matrix, b is the B0 value vector in slice k and x is the shim current vector. To break degeneracies, a z-dependency is introduced by including adjacent slices, hence fitting the dataset in a moving boxcar mode with a window of three. The first slice is fitted with relaxed constraints allowing ±50% of the available amplitudes, granting the slice to have a near-optimal solution x1. Following solutions xk are calculated by including prior information about xk-1: 1) xk-1 serves as the initial value for the new fit and 2) the channel bounds are set to vary maximally by ±10% of the maximum available amplitude around xk-1. Potential large current differences between the first/last slices are corrected in a final step in which a subset of the last slices is re-calculated with tightened constraints, adjusted such that the inter-slice limit is also maintained between the first/last slices (Fig. 1).

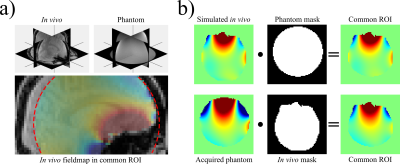
Due to a pending in vivo approval for the shim insert, the presented data were acquired in two steps (Fig. 2). An in vivo fieldmap was acquired from a consenting volunteer before shim insert installation and a DSU solution was calculated. After shim insert installation, the slice locations of the in vivo data were copied and the in vivo DSU shim currents were applied in a phantom. Subtraction of a static phantom fieldmap from the acquired DSU fieldmap yielded a map of the applied DSU shim fields for the in vivo DSU shim set.

Results

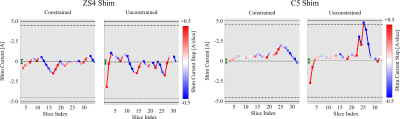
Our algorithm reduces the rate of change of DSU shim currents (Fig. 3) with minimal effect on achievable B0 homogeneity. For the common in vivo and phantom region-of-interest (ROI), the standard deviation of the predicted fieldmap was 15.8 Hz for the unconstrained vs. 15.9 Hz for the constrained case as compared to 24.93 Hz after 2nd order static shimming. It is to be noted that these value are higher than for an actual in vivo DSU acquisition at 3T, in which the largely homogeneous posterior part of the brain will be included in the ROI (cf. Fig. 2a).

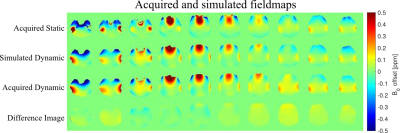
The EC reduction can be seen from the acquired DSU maps (Fig. 4) in which the differences between the predicted and acquired shim fields are marginal. These difference images are additionally confounded by calibration inaccuracies and actual EC effects are even smaller. On our system the zonal shims Z2, Z3 and Z4 generate a too strong dynamic B0 component and were excluded from optimization, but for the axial acquisitions this still enabled substantial homogeneity improvements (Fig. 5).

Discussion and conclusions

We have demonstrated that a tailored DSU shim calculation algorithm with prior information from previous slices is beneficial for EC reduction. Simulations and initial experiments have shown that the achievable B0 homogeneity is only marginally affected by the constraints.

For conventional DSU applications, our algorithm reduces the amount of the dynamic range of the shim amplifier that needs to be reserved for pre-emphasis. Our preliminary results indicate that pre-emphasis might even be necessary only for a dynamic Z0 component of the zonal shims which greatly reduces the pre-emphasis overhead. By fine-tuning the algorithm’s parameters, it may even be possible to perform DSU without pre-emphasis.

Acknowledgements

No acknowledgement found.

References

1. Stockmann, Jason P., et al. "A 32‐channel combined RF and B0 shim array for 3T brain imaging." Magnetic Resonance in Medicine 75.1 (2016): 441-451.

2. Juchem, Christoph, et al. "Dynamic multi-coil shimming of the human brain at 7T." Journal of Magnetic Resonance 212.2 (2011): 280-288.

3. Blamire, Andrew M., Douglas L. Rothman, and Terry Nixon. "Dynamic shim updating: a new approach towards optimized whole brain shimming." Magnetic Resonance in Medicine 36.1 (1996): 159-165.

4. Hetherington, Hoby P., et al. "Robust fully automated shimming of the human brain for high‐field 1H spectroscopic imaging." Magnetic Resonance in Medicine 56.1 (2006): 26-33.

Figures

Schematic illustration of the working principle of our algorithm: (1) A first solution (black dot) is calculated for one arbitrary slice with relaxed constraints (red box); (2) the algorithm advances with specific tight constraints to reduce ECs for each slice until the entire dataset is processed; (3) if the current difference between the first/last slice exceeds the ±10% threshold, the last N slices are re-calculated with adapted constraints such as to enforce compliance to the threshold. The constraints are specifically calculated for each shim at each slice, the exemplary data shown here is for the S3 shim.

a) Visualization of the 3D location of the head of the volunteer and the subsequently measured spherical water phantom. Both datasets share a common ROI with 91% volumetric overlap, as is illustrated by the masked in vivo fieldmap overlayed on the magnitude image where merely parts of the posterior brain are not covered by the common ROI; b) Slice-wise comparison between predicted and acquired shim fields is possible by masking both datasets with the common ROI mask.

DSU current plots for two exemplary shim channels showing the absolute slice-wise shim currents for all slices comparing the results of our proposed algorithm (“Constrained”) against results which are only limited by the hardware limits (“Unconstrained”). The green bar in each plot shows the magnitude of the maximum allowed shim step (0.5A) for the constrained algorithm and for each plot the magnitude of each shim step is color coded. It can be seen that the temporal evolution of shim currents using our proposed is much more favorable in terms of eddy current reductions.

Visualization of 10/33 exemplary slices: (1st row) the acquired in vivo fieldmap after 2nd order shimming; (2nd row) the simulated DSU shim fields to optimally cancel these residual inhomogeneities; (3rd row) the experimentally acquired DSU shim fields without pre-emphasis and (4th row) the difference between simulated and acquired DSU shim fields showing negligible residual field components with spatial variation and small (<14Hz) B0 offsets. It is to be noted that the already small residual differences are still a superposition of calibration inaccuracies (static) and EC (dynamic) effects, which means that the actual EC contributions are even smaller than depicted.

Comparison of the acquired in vivo 2nd order static shimming fieldmap against the predicted high order DSU shimmed fieldmap for the same exemplary slices as in Fig. 4 showing substantial homogeneity improvements.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0836