0801

Robust diffusion parametric mapping of motion-corrupted data using a deep-learning-based method
Ting Gong1, Hongjian He1, Zhiwei Li2, Qiqi Tong1, Zhichao Lin2, Yi Sun3, Feng Yu2, and Jianhui Zhong1,4

1Center for Brain Imaging Science and Technology, Key Laboratory for Biomedical Engineering of Ministry of Education, College of Biomedical Engineering and Instrumental Science, Zhejiang University, Hangzhou, China, 2Department of Instrument Science & Technology, Zhejiang University, Hangzhou, China, 3MR Collaboration NE Asia, Siemens Healthcare, Shanghai, China, 4Department of Imaging Sciences, University of Rochester, Rochester, NY, United States

Synopsis

Motion occurring during the acquisition of diffusion-weighted image volumes is inevitable. Deficient accuracy of volumetric realignment and within-volume movements cause the quality of diffusion model reconstruction to deteriorate, particularly for uncooperative subjects. Taking advantage of the strong inference ability of neural networks, we reconstructed diffusion parametric maps with remaining volumes after the motion-corrupted data removed. Compared to conventional model fitting, our method is minimally sensitive to motion effects and generates results comparable to the gold standard, with as few as eight volumes retained from the motion-contaminated data. This method shows great potential in exploiting some valuable but motion-corrupted DWI data.

Introduction

Diffusion imaging often requires many diffusion-weighted image (DWI) volumes leading to a long acquisition time with inevitable motion from human subjects. Conventionally, slow and between-volume movements are assumed and corrected by volumetric realignment to a template 1. However, it is known that this realignment does not correct all the motion-induced effects 2. Possible within-volume movements cause signal loss and zig-zag slices in a volume with interleaved acquisition 3-5. The reconstruction of a diffusion model with corrupted volumes causes blurry results whereas removing them is also unfavorable for model-fitting.

Method

In this study, we took advantage of the strong inference ability of neural networks to reconstruct diffusion parametric maps from motion-corrupted data. Two movement indicators in each DWI volume were calculated by root-mean-squared displacement across all intracerebral voxels relative to the first template volume (m1) and relative to the previous volume (m2). Whereas the DWIs were corrected by a realignment-based method assuming slow and between-volume motion, a large m2 suggested quick motion relative to the TR that breaks the slow-motion assumption, and a large m1 may introduce realignment-induced effects. Thresholds of the two indicators were set for selecting the DWIs for analysis. A hierarchical convolution neural network (H-CNN) designed for efficient diffusion kurtosis imaging (DKI) reconstruction was deployed to output all model-derived measures directly from the input DWIs.

Two subjects were scanned on a 3T MAGNETOM Prisma (Siemens Healthcare, Erlangen, Germany) equipped with a 64-channel head-neck coil. Subject 1 was scanned once lying still. Subject 2 was scanned twice sequentially, when lying still and when performing deliberate movements. Protocol: single-shot EPI sequence; TR/TE=7000/67 ms; FOV=210×210 mm2; slice number=50; resolution=2.5×2.5×2.5 mm3; diffusion weightings of b = 1000, 2000, and 3000 s/mm2 were applied in 30 directions, respectively, with six b=0 volumes entered, resulting in a total of 96 DWIs 6. The b=0 volume with an opposite phase-encoding direction was also acquired, leading to a total acquisition time of twelve minutes.

The acquired DWIs were initially preprocessed for the integrated correction of motion (between-volume) and distortion 7, during which process the realignment matrix was generated and the two indicators were calculated for each DWI volume. Different thresholds of m1 (1 – 8 mm) and m2 (0.5 – 4 mm) were set for selecting the less motion-affected DWIs from motion data of subject 2 to test the robustness of model fit and the H-CNN. The corresponding DWIs of Subject 1 were used for network training. All DKI model-fitting was implemented in DKE (http://academicdepartments.musc.edu/cbi/dki/dke.html) using a constrained linear least square method 8. The training labels of Subject 1 and reference standard of Subject 2 were reconstructed from all the 96 DWIs in their still condition by model-fitting. Keras 9 was used as the toolbox for training and testing with Tensorflow 10 running backend. The time was 79.9 - 273.5 s for training and 0.7 - 1.2 s for testing, with 8 - 96 input DWIs performed on a NVIDIA Tesla k20c platform.

Results

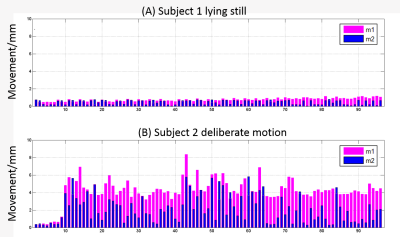
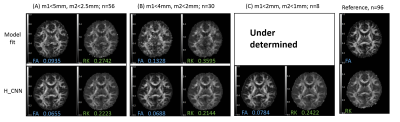
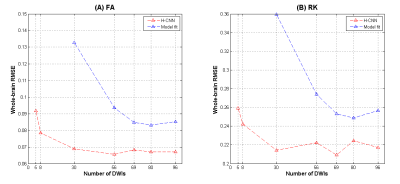
Figure 1 shows the two movement indicators of Subject 1 lying still and Subject 2 with deliberate motions that constitute the training and testing datasets, respectively. Several DWI volumes comprising different extents of motion that may cause the image quality to deteriorate are depicted in Figure 2. Figure 3 shows the fractional anisotropy (FA) and radial kurtosis (RK) maps from model-fitting and the H-CNN. When more DWIs with relatively large movements were retained for model fitting, the estimated maps showed a low contrast with a blurred boarder, whereas a loss of structure is also prominent, with large numbers of DWIs removed. For the H-CNN, a relatively stable performance with a fine retained structure was achieved. The whole-brain root-mean-squared errors in Figure 4 further demonstrate the superiority of the H-CNN for the motion-corrupted data. It should be noted that while we acquired 96 DWIs for the demonstration of this comparison study, 30 - 60 DWIs are often acquired in the clinical environment, which is more difficult for a model-fitting method with large movements.

Discussion

Our method achieved a comparable estimation performance to fully sampled results with large numbers of DWI volumes removed. Compared to the method attempted to correct within-volume movements 4-5, our method directly avoids the introduction of other effects and is quick in its post-processing time. Further experiments with more elaborate characterization of motion types and a comparison to the results from fitting with corrected data should be conducted in future studies.

Conclusion

This method shows great potential to make full use of the valuable data from less cooperative subjects such as infants, children, and certain motion-prone patients.

Acknowledgements

This work was supported by the National Key R&D Program of China (2017YFC0909200), National Natural Science Foundation of China (81401473, 91632109) and the Fundamental Research Funds for the Central Universities (2017QNA5016).

References

1. Friston K J, Ashburner J, Frith C D, et al. Spatial registration and normalization of images. Human Brain Mapping, 1995, 3(3): 165-189.

2. Friston K J, Williams S C, Howard R, et al. Movement-related effects in fMRI time-series. Magnetic Resonance in Medicine, 1996, 35(3): 346-355.

3. Kim B, Boes J L, Bland P H, et al. Motion Correction in fMRI via Registration of Individual Slices Into an Anatomical Volume. Magnetic Resonance in Medicine, 1999, 41(5): 964-972.

4. Andersson J L, Graham M S, Zsoldos E, et al. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage, 2016: 556-572.

5. Andersson J L, Graham M S, Drobnjak I, et al. Towards a comprehensive framework for movement and distortion correction of diffusion MR images: Within volume movement. NeuroImage, 2017: 450-466.

6. Caruyer E, Lenglet C, Sapiro G, et al. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine, 2013, 69(6): 1534-1540.

7. Andersson J L, Sotiropoulos S N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 2016: 1063-1078.

8. Tabesh A, Jensen J H, Ardekani B A, et al. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magnetic Resonance in Medicine, 2011, 65(3): 823-836.

9. Chollet F et al., “Keras,” https://github.com/fchollet/keras, 2015.

10. Abadi M, Barham P, Chen J, et al. TensorFlow: a system for large-scale machine learning. operating systems design and implementation, 2016: 265-283.

Figures

Figure 1. Demonstration of the two movement indicators of the 96 DWIs from (A) Subject 1 lying still and (2) Subject 2 with deliberate motion, in sequential image volumes (m1 is the whole-brain root-mean-squared displacement relative to the first template volume, and m2 is the root-mean-squared displacement relative to the previous volume, both of which were computed during the realignment-based motion correction). While a large m1 may be accumulated from the preceding DWIs, a large m2 indicates quick motion, which is very likely to cause within-volume deterioration.

Figure 2. Diagram of several DWIs. (A) The 72nd DWI with a large m1, (B) the 60th DWI with a large m2, and (C) the 43rd DWI with both a large m1 and m2. Whereas the volumes of the large m2 show prominent within-volume motion-induced jagged edges in the sagittal and coronal view (B, C) and signal loss (C), the volume of the large m1 alone does not show any prominent contamination on visual inspection (A). However, the large m1 may introduce realignment-induced effects. For subjects in the still condition, generally m1< 2 mm, and m2< 1 mm.

Figure 3. The FA (blue) and RK (green) maps estimated from model-fitting and the H-CNN with different numbers of DWIs (56, 30, 8) selected by different m1 and m2 thresholds. The number under each map is the whole-brain root-mean-squared error (RMSE) compared to the reference standard reconstructed from model-fitting with the full dataset (96 DWIs) in the still condition. The H-CNN method is rather robust against severe motion effects and largely decreased DWI number compared to the model fit.

Figure 4. The whole-brain RMSE of FA and RK maps as a function of the number of DWIs selected by different m1 and m2 thresholds. The 96 is from all the DWIs; 80 (m1 < 8 mm, m2 < 4 mm); 69 (m1 < 6 mm, m2 < 3 mm); 56 (m1 < 5 mm, m2 < 2.5 mm); 30 (m1 < 4 mm, m2 < 2 mm); 8 (m1 < 2, m2 < 1 mm); and 5 (m1 < 1, m2 < 0.5 mm). The H-CNN offers considerable improvement, even with only eight volumes retained.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0801