0750

Multishot high-resolution brain diffusion-weighted imaging using phase regularized reconstruction
Yuxin Hu1,2, Xiaole Wang3, Evan G. Levine1,2, Qiyuan Tian1,2, Valentina Taviani4, Frank Ong5, Shreyas Vasanawala1, Jennifer A McNab1, Bruce L. Daniel1,6, and Brian Hargreaves1,2,6

1Department of Radiology, Stanford University, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 3Biomedical Engineering, Tsinghua University, Beijing, China, 4GE Healthcare, Menlo Park, CA, United States, 5Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, CA, United States, 6Department of Bioengineering, Stanford University, Stanford, CA, United States

Synopsis

Multishot imaging has been shown to provide high resolution diffusion-weighted images (DWIs) with reduced distortion, however, significant aliasing artifacts and signal cancellation still occur due to the mismatch of the motion-induced phase between different shots. The reconstruction becomes non-convex and intractable to solve when this phase is included into the forward model. The goal of this work is to solve this problem by circumventing the challenging phase estimation step. The brain and breast examples demonstrate that this can be efficiently achieved using a locally low-rank reconstruction approach.

Introduction

Several SENSE-based methods without navigators have been proposed for multishot brain DWI1-3, in which the results of parallel imaging on each shot are used for phase estimation. These methods may fail when phase variations are more complex, or SNR is low. As an alternative, we use an efficient matrix-completion approach (“shot-LLR”) for robust phase estimation. This is used to initialize a non-convex formulation of multishot reconstruction that enables joint estimation of the magnitude and phase, with a L1-wavelet penalty on both. We demonstrate the technique for high-resolution DTI (0.8mm isotropic) and double diffusion encoding.

Theory

We first use locally low-rank regularization to do phase estimation:

$$\min_{x{1},...x_{Ns}}\sum_{i=1}^{Ns}||D_{i}FSx_{i}-y_{i}||_2^2+\lambda\sum_{b\in W}||R_{b}(x)||_*$$

where Rb4,5 constructs a matrix with images of all shots at index b, as shown in Fig. 1a. Since the motion-induced phase is spatially smooth in many blocks, the sum of ranks of these matrices is low. Di, xi and yi are the sampling operator, image to be reconstructed, and the data acquired in the ith shot, F is the Fourier transform, S are sensitivity maps, lambda is a regularization parameter, and W is the set of all non-overlapping blocks which uniformly tile the image domain. This convex problem is guaranteed to converge to the global minimal, and the use of this relaxed model also gives a more robust estimation.

Next, the phase of each shot, and the average shot image amplitude from shot-LLR are used to initialize the phase and magnitude for the following:

$$\min_{m,\theta_{1},...\theta_{Ns}}\sum_{i=1}^{Ns}||D_{i}FSm\cdot e^{j\theta}-y_{i}||_2^2+\lambda_{1}g_{m}(m)+\lambda_{2}\sum_{i=1}^{Ns}g_{\theta}(\theta_{i})$$

where m and θ are the magnitude and phase to be reconstructed, Ns is the total number of shots, gm and gθ are the regularization terms on magnitude and phase, and λ1 and λ2 are corresponding regularization parameters. While different regularizers can be applied, here we use the l1-norm of wavelet transform for both magnitude and phase6.

Alternating minimization with respect to the magnitude and phase separately is used to solve the above problem, and for each sub-problem, we use the proximal gradient method7,8.

The phase constraint integrates partial Fourier reconstruction by using phase cycling to avoid phase wraps7. In each iteration, a random phase shift is added to shift the position of phase wraps. The overall flow is shown in Fig. 1b.

Methods

All scans used a 3T GE MR750 scanner using a 2D DW EPI sequence.

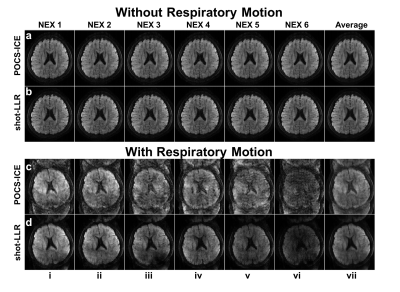
To evaluate the performance of shot-LLR on data with large motion-induced variations, we performed two 4-shot experiments with: nex=6, resolution=0.85x0.85x3mm3, number-of-shots=4, b-value=1000s/mm2. The volunteer was asked to breath normally for the first time, and deeply for the second time to induce respiratory motion (and phase variations).

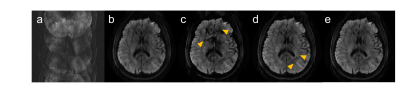
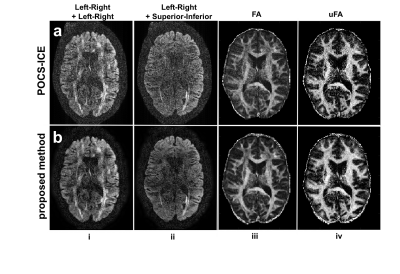
4-shot double-diffusion-encoding (DDE) data were acquired on a volunteer using a 32-channel head coil with: resolution=1×1×2mm3, nex=1, and for each diffusion encoding pair: b=1000 s/mm2, 60 parallel and 60 orthogonal encoding directions.

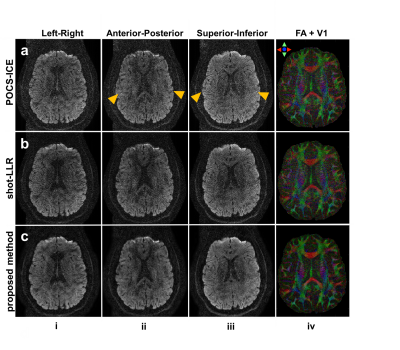
Diffusion tensor imaging data were acquired on a volunteer using a 32-channel head coil with: resolution=0.8x0.8x0.8mm3, number of shots=4, b-value=1000s/mm2, nex=1 and 45 diffusion encoding directions uniformly distributed on a sphere.

POCS-ICE was implemented for comparison3, and homodyne is used to fill the un-acquired half k-space10. Shot-LLR was implemented based on BART11. The numbers of iterations are 200 for POCS-ICE and shot-LLR, and 50 for the proposed method, with reconstruction times about 2 minutes per slice.

Results and Discussion

As shown in Fig. 2, for motion corrupted data, there are obvious aliasing artifacts in POCS-ICE. Shot-LLR has significantly fewer artifacts, suggesting that shot-LLR can handle more complicated phase variations between shots. Such an advantage comes from the fact that only a low-rank constraint is used and no explicit phase estimation is needed.

Fig. 3 shows the 4-shot brain DW image reconstructed by different methods in Figure 1. Using shot-LLR as initialization and phase cycling (Fig. 3e) gives the best results.

The proposed method shows improved DDE images, FA maps and μFA maps compared with POCS-ICE as shown in Fig. 4.

Figure 5 shows a representative slice of submillimeter-resolution diffusion-weighted images and corresponding V1-encoded FA maps reconstructed with different methods. Images from the proposed method is least noisy and the V1-encoded FA map maintains the detailed structure.

Conclusion

We introduced a new phase regularized method to reconstruct multishot DWI with LLR matrix completion as initialization. It is especially beneficial for high-resolution, submillimeter brain DTI and DDE imaging.

Acknowledgements

Research support from R01-EB009055, P41-EB015891 and GE Healthcare.

References

1. Butts, Kim, et al. "Diffusion‐weighted interleaved echo‐planar imaging with a pair of orthogonal navigator echoes." Magnetic resonance in medicine 35.5 (1996): 763-770. 2. Atkinson, David, et al. "Nonlinear phase correction of navigated multi‐coil diffusion images." Magnetic resonance in medicine 56.5 (2006): 1135-1139.

3. Guo, Hua, et al. "POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI." Magnetic resonance in medicine 75.1 (2016): 169-180. 4. Liang ZP. Spatiotemporal imaging with partially separable functions. IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 4th IEEE; 2007.

5. Trzasko, Joshua D., and Armando Manduca. "Calibrationless parallel MRI using CLEAR." Signals, Systems and Computers (ASILOMAR), 2011 Conference Record of the Forty Fifth Asilomar Conference on. IEEE, 2011. 6. Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.

7. Combettes PL, Pesquet JC. Proximal Splitting Methods in Signal Processing. in “Fixed-Point Algorithms for Inverse Problems in Science and Engineering”, pp. 185–212. Springer New York, New York, NY, 2011.

8. Parikh N, Boyd S. Proximal algorithms. Foundations and Trends in optimization 2013; .

9. Ong, F., Cheng, J., & Lustig, M. (2017). General Phase Regularized Reconstruction using Phase Cycling. arXiv preprint arXiv:1709.05374.

10. Noll, Douglas C., Dwight G. Nishimura, and Albert Macovski. "Homodyne detection in magnetic resonance imaging." IEEE transactions on medical imaging 10.2 (1991): 154-163.

11. BART Toolbox for Computational Magnetic Resonance Imaging, DOI: 10.5281/zenodo.592960

Figures

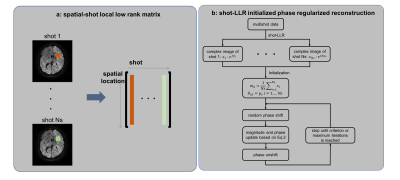
Figure 1a: “Shot-LLR” constructs a “spatial-shot” matrix containing a block of pixels from each of the shots. With images from all shots, we define an operator, which extracts one small block in the image domain, reshapes it into a vector, and concatenates vectors from all shots into a matrix. With n pixels in one block, and Ns shots, an n-by-Ns spatial-shot matrix is constructed.

b: Flow chart of the proposed phase regularized method using shot-LLR as initialization and phase cycling to enable half Fourier acquisition.


Figure 2. 4-shot images reconstructed by different methods without (a, b) and with (c, d) severe respiratory motion. The first six columns show images from different nex and the last column shows the averaged images of all nex. Both methods achieve similar results without motion. When there is severe motion, strong aliasing artifacts can be seen in POCS-ICE (c), while shot-LLR (d) has a more robust performance.

Figure 3. 4-shot brain DW images reconstructed by Fourier transform (a), shot-LLR (b), proposed method with zero-filled data as initialization (c), proposed method with shot-LLR as initialization and without phase cycling(d) and proposed method with shot-LLR as initialization and phase cycling(e) (res: 0.85 x 0.85 x 3 mm3, b-value = 1000 s/mm2, nex = 1). The yellow triangles identify errors.

Figure 4. 2 out of 120 directions 4-shot DDE images (res: 1 x 1 x 2 mm3, total b-value = 2000 s/mm2, nex = 1), and corresponding FA maps and μFA maps with POCS-ICE and proposed method. The noise level in the proposed method is significantly decreased.

Figure 5. 3 out of 45 directions of 4-shot DW images (res: 0.8 x 0.8 x 0.8 mm3, b-value = 1000 s/mm2, nex = 1), and corresponding V1-encoded FA maps with POCS-ICE, shot-LLR and proposed method. Some residual aliasing artifacts still exist in POCS-ICE as indicated by the yellow triangles, and images from the proposed method are least noisy and the V1-encoded FA map maintains the detailed structure.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0750