0748

Quantifying diameter overestimation of undulating axons from synthetic DW-MRI

Alonso Ramirez-Manzanares¹, Mario Ocampo-Pineda², Jonathan Rafael-Patiño³, Giorgio Innocenti^3,4,5, Jean-Philippe Thiran³, and Alessandro Daducci^2,3,6

¹Computer Science, Centro de Investigación en Matemáticas A.C., Guanajuato, Mexico, ²University of Verona, Verona, Italy, ³Signal Processing Lab (LTS5), École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, ⁴Department of Neuroscience, Karolinska Institutet, Stockholm, Sweden, ⁵Brain and Mind Institute, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, ⁶University Hospital Center (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland

Synopsis

This study aims to provide to the research community quantitative measurements about the axon diameter overestimation due to the straight-cylinder assumption usually made in state-of-the-art models for diameter mapping with DW-MRI. Our methodology uses a Monte Carlo diffusion simulator to compute the diffusion weighted magnetic resonance signals of undulating axons. We use in our experiments plausible tissue values, we also explore a broad parameter set that depicts undulation. The results of this study provide useful information to understand the differences between the estimators from histology vs. the estimated diameters when using the model assumption of simple shaped axons.

Introduction and Purpose

The diffusion-weighted (DW) magnetic resonance imaging (MRI) allows estimating White Matter (WM) microstructure parameters such as axon diameters^1,2. To the best of our knowledge, there are still unquantified large differences among the estimators computed from DW-MR data and the gold-standards (GS) obtained from histology, see Fig. 9 in². One reason of such discrepancies is the oversimplification of the axon’s structure as straight parallel axons. The Monte Carlo DW Simulations (MCDS) allow to experiment with complex WM environments, thus to compute realistic DW-MR signals³. The overestimation on the axon diameters due to undulation has been suggested previously in^4,5, however, to the best of our knowledge, no quantitative experimentation has been developed in this direction. In a nice study about the repercussion of axon undulation the analytical formulation of the ensemble average propagator was deducted⁴, nevertheless, the assumption of zero diameter axons makes that formulation non suitable for this study.

Methods

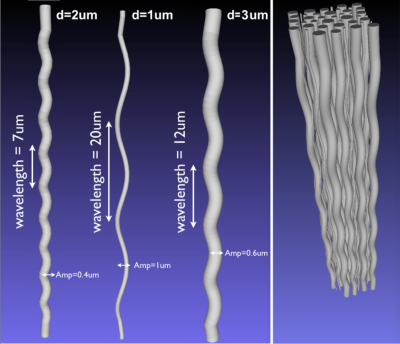
Axon geometries: We use the helical undulation parameterization of an axon along $$$z$$$ $$$\mathbf{U}(z) = \left(A_x\cos(2\pi z/L) , A_y\sin(2\pi z/L) , z \right)$$$, where $$$L$$$ denotes the wavelength and $$$A_x$$$,$$$A_y$$$ denote the amplitudes in $$$x$$$ and $$$y$$$, respectively⁴, we build a synthetic database with DW-MR signals associated with a diverse range of diameters and parameterized undulations, it also includes undulation values observed in actual tissue. Undulation Parameterization: To systematically characterize the effects of undulation, the parameters are varied as follows: amplitudes in [0,5]μm, wavelengths in [7,60]μm, and the diameters in the range of anatomical interest [1,3]μm. Protocol: The proposal is tested for a PGSE DW-MR protocol optimized for axonal diameter estimation with G=300mT/m, TE=35.9ms⁶. The bulk diffusivity is 0.6μm$$$^2$$$/ms. MCDS Settings: The number of particles in the MCDS, around 14k per each 60μm axon piece, was optimized to keep the MCDS variance smaller than 3% of the signal magnitude. The number of particle steps was set T=3k. Model Fitting: The intracellular signals are then fitted by a Brute Force (BF) approach to the straight cylinder model^7,11 where the unknowns are the diameter, $$$d$$$ , and the axial diffusivity coefficient (bulk diffusivity) $$$D_{||}$$$. The BF approach reports the optimal configuration {$$$d^*, D^*_{||}$$$} from the sets $$$\hat d$$$ = {0.1,0.2,0.3,…,18.0}μm and $$$\hat D_{||}$$$ = { 0.3,0.35,0.40,…,0.9}μm$$$^2$$$/ms that generates the closest PGSE signal (smallest MSE) to the MCDS signal.

Experiments and Results

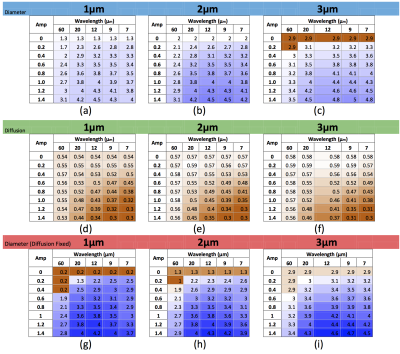
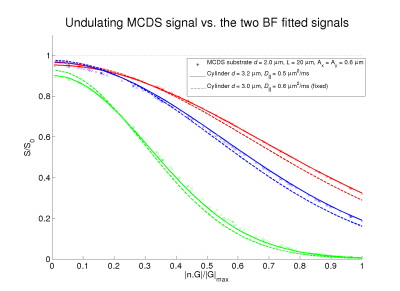
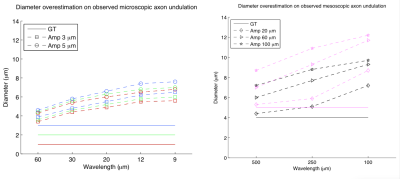
Examples of used substrates are in Figure 1. General undulation characterization: We performed noise free experiments with isolated intracellular signals. Table (a)-(c) in Figure 2 reports the diameter overestimation due to undulation for different configurations, (d)-(f) shows the computed $$$D_{||}$$$ values, respectively. Note that Figure 2 indicates the expected overestimation even in the perfect estimation scenario. Fixing the bulk diffusivity: Some methodologies^8,2 fixed the bulk diffusivity of the cylinder model ($$$D_{||}$$$) and estimate only the diameter, the last row in Figure 2 shows the effect on the diameter overestimation of that strategy when $$$D_{||}$$$ is set as the ground-truth value, interesting, one can see that, by using the right $$$D_{||}$$$ values it is possible to reduce the diameter overestimation. Signal Fitting Quality: The left and right panels of Figure 3 show examples of MCDS signals and the signal for the best BF fit when all the parameters are estimated, and, when only the diameter is estimated; we note that in the second case the signal fitting is poor. Observed axon undulations: The results of the experiments in Figure 4 report the overestimation on some axon geometries observed in actual tissue samples^4,12,13 in microscopic and mesoscopic scale. Diameter distributions: Finally, we compute the parameters by the BF approach that best fit the intracellular signal from 46 (amplitude=0.3μm) and 54 (amplitude=0.2μm) undulating axons with wavelengths 12 and 20μm (see Figure 1), and with plausible gamma distributed diameters inside a periodic voxel with size 10x10x40μm. We computed the ideal-axon-diameter-index α and estimated indices a' from the BF, see². For instance, on amplitude=0.3μm and wavelength=20μm, a'=3.5μm which is significantly larger than α=1.45μm due to undulation.

Conclusions

Our results indicate that overestimation on the computed diameter due to axon undulation is significant (≈2 times) and could distort the anatomical information on histological validations, this may partially explain (apart from tissue-fixation issues) the differences, for instance, in Fig. 9 in². For 1μm diameters exist overestimation even on low-undulation cases due to the non-capability of the PGSE protocol to differentiate small axons signals. When a well-approximated value of the intracellular bulk-diffusivity is known, the signal discrepancy (Figure 3) could indicate a poor undulation modeling. We consider the future work should be focused on the validation of dispersion strategies^9,10 to overcome the undulation effects on diameter estimation.

Acknowledgements

Ramirez-Manzanares was partially supported by SNI-CONACYT, Mexico and by the Swiss National Science Foundation international short visit grant (IZK0Z2_175121).

References

1. Assaf Y., Blumenfeld-Katzir T., et al. Axcaliber: A method for measuring axon diameter distribution from diffusion MRI. Magnetic Resonance in Medicine. 2008; 59(6): 1347-1354.

2. Alexander D.C., Hubbard P.L., et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage. 2010; 52(4): 1374-1389.

3. Jonathan Rafael-Patino. Design and Validation of a Robust Di usion-Weighted-MRI Monte Carlo Simulator. Master Thesis at Centro de Investigation en Matematicas A. C. 2015; http://www.cimat.mx/es/Tesis_digitales .

4. Nilsson M, Lätt J., et al. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR in Biomed. 2012; 25(1): 795-805.

5. Nilsson M., van Westen D., et al. The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magn. Reson. Mater. Phy. 2013, 26(1), 345-370.

6. Dyrby T B. and Sogaard L.V., et al. Contrast and stability of the axon diameter index from microstructure imaging with diffusion MRI. Magnetic Resonance in Medicine. 2013; 70(3): 711-721.

7. van Gelderen P., DesPers D., et al. Evaluation of Restricted DIffusion in Cylinders. Phosphocreatine in rabbit leg muscle. Magnetic Resonance. 1994; 103: 255-260.

8. Zhang H., Schneider T., et al. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012; 61(4): 1000-1016.

9. Zhang H, Hubbard P. L., et al. Axon diameter mapping in the presence of orientation dispersion with diffusion MRI. NeuroImage, 2011, 56(1), 1301-1315.

10. Ocampo-Pineda M., Daducci A., et al. Estimation of a novel set of intra and extracellular diffusivity parameters from modern DW-MRI. ISMRM 2017, No. 1827. Hawaii, U.S.A.

11. Alexander D.C. Modelling, Fitting and Sampling in Diffusion MRI. Springer. Visualization and Processing of Tensor Fields. 2009: 3-20.

12. Jeffery G. PNS features of rodent optic nerve axons.J. Comp. Neurol. 1996; 366(2): 370-378.

13. Haninec P. Undulating course of nerve fibres and bands of Fontana in peripheral nerves of the rat. Anat. Embryol. 1986; 174(3): 407-411.

Figures

Figure 1. Examples of the substrates representing undulating axons used in this study. Left panel illustrates the parameters for different configurations. Right panel shows a periodic substrate in a 10x10x40μm voxel from plausible gamma distributed diameters.

Figure 2. Tables of the estimated values of axon diameter $$$d$$$ and axial diffusivity $$$D_{||}$$$ for different amplitudes and wavelengths. The 3 columns correspond to 1, 2, and 3μm diameter undulating axons. Brown and blue color indicates underestimation and overestimation, respectively. (a)-(c) Reports the overestimation on the diameter when the straight cylinder models is assumed, (d)-(f) shows the computed $$$D_{||}$$$ values. Last row, presents the diameter estimation when the $$$D_{||}$$$ is set to the correct value. Note the significant overestimation in diameter for many undulation configurations.

Figure 3. The undulating MCDS DWMR-signal (dot-pattern) for $$$d$$$=2μm (parameters in Figure) and the corresponding straight cylinder signal computed by the BF approach. The continuos line is the solution when both the diameter, $$$d$$$, and the axial diffusivity, $$$D_{||}$$$ are computed, the dashed line is the signal estimated when $$$D_{||}$$$ is fixed to the ground-truth value and only $$$d$$$ is estimated. Note that, the signal fit is poor in the second case, this could be advantageous because it highlights a poor modeling when a good approximation of $$$D_{||}$$$ is available. Similar results are obtained for different undulation configurations (not shown).

Figure 4. Plot of the overestimated diameter for observed undulation axon geometries^4,12,13. Horizontal continuous lines denote the ground-truth diameters (each one of different color). Panel in the left contains (among others) diameters estimations for undulation observed in the optic nerve (microscopic scale) with amplitudes between 3-5μm, wavelength around 30μm and $$$d$$$=1μm; right panel contains (among others) the diameter values estimated under undulation configurations observed in the sciatic nerve (mesoscopic scale) with amplitudes around 20-100μm, wavelengths around 100μm and diameters around 4-5μm.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

0748