Synopsis

We present a numerical framework for validation of diffusion models applied to biological tissues. By performing Monte Carlo simulations in a geometry created by automated segmentation of 3-dimensional mouse brain electron-microscopy images, we study the time-dependence of the diffusion coefficient and kurtosis along individual white matter axons, with or without orientation dispersion. Simulation results, together with the analysis of spatial correlations of axonal cross-section variations along axons, point at the short-range disorder in restrictions to diffusion, and agree with theoretical predictions. Our results are consistent with diffusion time-dependence observed in in vivo human brain data.

Purpose

Diffusion MRI (dMRI) is sensitive to a length scale of microns, and is an indispensable in vivo technique for evaluating microstructure in biological tissues. For validating various diffusional models developed for white matter (WM), previous numerical simulations were performed either in simple geometries (circles/ellipses/cylinders/spheres/ellipsoids)$$$\,$$$[1-4], or in 2d realistic micro-geometry reconstructed from light or electron microscopy$$$\,$$$[5-6]. However, simulations in a realistic three-dimensional microstructure, that reflects genuine tissue properties, have been missing.

Here we present a framework for segmenting axons from sequential-slice election microscopy (SSEM) images in the corpus callosum (CC) of a mouse brain. By performing Monte Carlo (MC) simulations in the obtained realistic 3d intra-axonal space (IAS), we study the time-dependence of diffusion coefficient and kurtosis along axons with or without axonal orientation dispersion. Having full control of tissue microstructure allows us for the first time to validate theory and previously reported human brain data$$$\,$$$[7-8] .

Methods

$$$\bf{SSEM}$$$

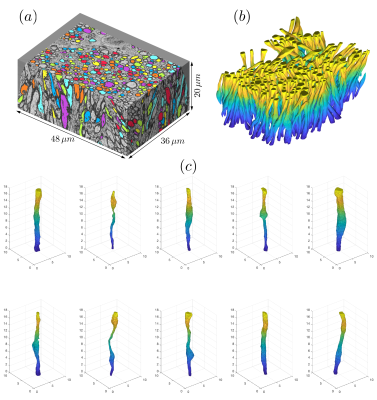
A female 8-week-old C57BL/6 mouse was sacrificed and fixed by transcardiac-perfusion. The genu of CC was excised and analyzed with a scanning electron microscope (Zeiss Gemini-300), which acquired 401 consecutive images of$$$\,6000\times8000\,$$$pixels. Part of the data was discarded due to distortion, leading to a volume (Fig.1a) of$$$\,36\times48\times20\,\mu$$$m$$$^3\,$$$with $$$6\times6\times100\,$$$nm$$$^3$$$-resolution.

$$$\bf{IAS\,Segmentation}$$$

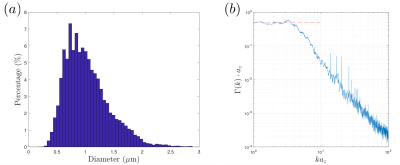
Data was downsampled to$$$\,24\times24\times100\,$$$nm$$$^3$$$-resolution before segmentation. To segment long axons passing through all slices, we employed diffusion: We manually seeded an initial position per axon within the central slice (451 seeds), and filled the IAS by cubic-lattice-hopping diffusion trajectories of 1000 particles per axon, confined by a myelin mask obtained by expectation-maximization algorithm. Segmented axons with imperfect myelin mask were deleted (~135) by proofreading, resulting in an IAS mask of 216 fully segmented long axons ($$$>20\,\mu$$$m in length, discarded ~100 short ones). The IAS mask was downsampled into$$$\,(0.1\,\mu$$$m$$$)^3$$$-resolution, and transformed into 3d polyhedra by tetrahedral-filling (Fig.1b). The effect of orientation dispersion was controlled by subsequent realigning axons along the z-axis (Fig.1c). To determine the structural universality class of geometries along axons, we calculated the power-spectrum$$$\,\Gamma(k)=\tilde{\rho}(-k)\tilde{\rho}(k)/L$$$, where$$$\,\tilde{\rho}(k)\,$$$is the Fourier transform of$$$\,\rho(z)$$$, which is the normalized IAS cross section along axons (Fig.2b).

$$$\bf{Numerical\,Simulation}$$$

MC simulations of random walkers were implemented in Matlab in continuous space bounded by the boundary of polyhedral IAS, and validated in a polyhedron-approximated cylinder (Fig.3). Next, simulations were performed inside 216 IAS polyhedra (Fig.1c). $$$1.1\times10^5$$$ random walkers were distributed in proportion to axonal volume. Each particle diffused over $$$1.25\times10^5$$$ steps with a duration$$$\,8\times10^{-3}\,$$$ms and a step length$$$\,0.098\,\mu$$$m. Maximal diffusion time$$$\,t=100\,$$$ms. Axo-plasmic diffusivity $$$D_0=2\,\mu$$$m$$$^2$$$/ms. Total calculation time ~35hours on 200 CPU cores of a high-performance-computing cluster.

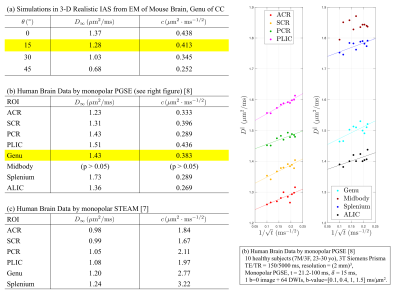
Diffusivity and kurtosis were estimated by cumulants ($$$\langle\,x^2\rangle$$$,$$$\,\langle\,x^4\rangle$$$). To simulate dispersion, we calculated total diffusivity and kurtosis when axons oriented on a cone with a polar angle$$$\,\theta=[0^\circ,15^\circ,30^\circ,45^\circ]\,$$$(no dispersion to high dispersion). We then compared simulation results with theory (described below) and previously published human studies using mono-polar PGSE$$$\,$$$[8] and STEAM$$$\,$$$[7] (Table 1b-c).

$$$\bf{Theory}$$$

The non-Gaussian diffusion along WM tracts at long diffusion time$$$\,t$$$ probes the geometry and length scale of restrictions along axons$$$\,$$$[9]. Randomly-positioned restrictions along axons (short-range disorder in 1d) yield the following functional form$$$\,$$$[9] for the axial diffusivity $$D^\parallel(t)\simeq\,D_\infty+c\cdot\,t^{-\vartheta}\,,\quad\quad(1)$$ and axial kurtosis$$$\,$$$[10]: $$K^\parallel(t)\simeq\,K_\infty+\frac{2c}{D_\infty}\cdot\,t^{-\vartheta}\,,\quad\quad(2)$$ characterized by the dynamical exponent $$$\vartheta=1/2$$$. Here$$$\,D_\infty\,$$$is the bulk diffusivity at$$$\,t\to\infty$$$,$$$\,c\,$$$is the strength of restrictions, and$$$\,K_\infty\,$$$is the kurtosis at $$$t\to\infty$$$, resulting from variances of$$$\,D_\infty^{(i)}\,$$$between different axons. The time-dependence of$$$\,K^\parallel(t)\,$$$is completely determined by the effective-medium parameters ($$$D_\infty,\,c$$$). We tested this prediction using simulations.

Results

Fig.2a shows the diameter histogram of long axons, and Fig.2b shows the 1-dimensional power spectrum along axons, where the red-dashed line indicates that$$$\,\Gamma(k)\propto\,k^p\,$$$approaches a plateau at$$$\,k\to0\,$$$(structural exponent$$$\,p=0\,$$$equivalent to short-range disorder), predicting the dynamical-exponent$$$\,\vartheta=(p+d)/2=1/2\,$$$in dimension$$$\,d=1$$$, Eqs.(1-2)$$$\,$$$[9].

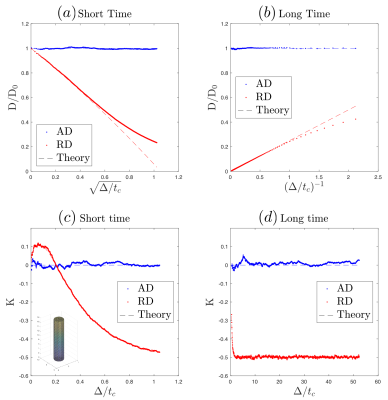
Fig.3 validates our MC simulations in a polyhedron-approximated cylinder, reproducing known short-$$$t\,$$$[11] and long-$$$t\,$$$[12] theoretical results.

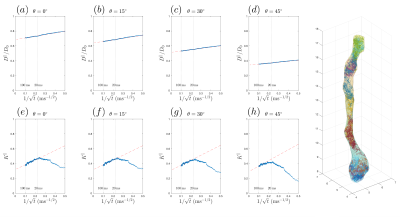
Fig.4a-d shows that, in realistic IAS polyhedra, simulated$$$\,D^\parallel(t)\,$$$is consistent with the time-dependence in Eq.(1) (fitted red-dashed line) even for highly dispersed axons ($$$\theta=45^\circ$$$). Table 1a shows corresponding fitted parameters ($$$D_\infty$$$,$$$\,c$$$), consistent with the human data in Table 1b.

To confirm that the micro-geometry along axons falls into the short-range-disorder universality class$$$\,$$$[9], we predicted the time-dependence of simulated $$$K^\parallel(t)$$$ based on effective medium parameters from$$$\,D^\parallel(t)\,$$$in Table 1a. The theoretical prediction (slope$$$\,2c/D_\infty\,$$$of red-dashed line with respect to$$$\,1/\sqrt{t}$$$), based on Eq.(2), is shown in Fig.4e-h, agreeing with the time-dependence at long$$$\,t\,$$$from MC, when dispersion angle$$$\,\theta\leq30^\circ$$$.

Discussions and Conclusions

Simulation results are consistent with in vivo measurements and theoretical predictions: diffusion along axons, either with or without dispersion, is characterized by 1d short-range disorder and the$$$\,\vartheta=1/2\,$$$dynamical exponent, Eqs(1)-(2).

The proposed framework of axon segmentation and MC simulation in 3d realistic SSEM microstructure suggests a new validation method that could be extended for various other MRI contrast mechanisms, e.g. magnetization transfer, susceptibility, relaxation, exchange, etc.

Acknowledgements

References

[1] Li, J. R., et al., JMR, 248, 54-65 (2014)

[2] Harkins, K. D. & Does, M. D., Phys Med & Bio, 61, 4729-4745 (2016)

[3] Lin, M., et al., MRM, 76, 290-300 (2016)

[4] Palombo, et al., Proc ISMRM, 25, 1087 (2017)

[5] Chin, C. L., et al., MRM, 47, 455-460 (2002)

[6] Xu, T., et al., MRM (2017)

[7] Fieremans, E., et al., NeuroImage, 129, 414-427 (2016)

[8] Papaioannou, A., et al., Proc ISMRM, 25, 0723 (2017)

[9] Novikov, D. S., et al., PNAS, 111(14), 5088-5093 (2014)

[10] Novikov, D. S. & Kiselev, V. G., NMR Biomed, 23, 682-697 (2010)

[11] Mitra, P. P., Phys Rev B, 47(14), 8565-8574 (1993)

[12] Callaghan, P. T., JMR A, 113, 53-59 (1995)

[13] Burcaw, L. M., et al., NeuroImage, 114, 18-37 (2015)

[14] Lee, H. H., et al., Proc ISMRM, 25, 0839 (2017)