Synopsis

In this work, we introduce a new framework that we developed to use numerical simulations to investigate the complexity of brain tissue at a microscopic level with a detail never realised before. Directly inspired by the advances in computational neuroscience for modelling brain cells, the proposed toolbox enables numerical simulation of molecular diffusion within realistic digitalised brain cells, such as neurons and glia. Here we show a select set of examples offered by this new toolbox to demonstrate its versatility and potentiality. Further development is ongoing, which will support even more realistic conditions and fully digitalised tissues.

Introduction

This work introduces a general and versatile computational framework to simulate diffusion-weighted NMR (DW-NMR) signal in realistic digital models of brain tissue.

The relationship between the macroscopic DW-NMR signal and brain tissue microstructure is complex. Over the last decade, a wide variety of mathematical models have been proposed to describe this relationship. However, the validity of their underlying model assumptions is still under debate. Objective data-driven assessment of these assumptions, often hard to conduct experimentally, remains an important yet unsolved challenge. In this context, advanced numerical simulation can provide a powerful tool to test the limits of a specific biophysical model and aid the design of experimental strategies as well as inspiring new biophysical models for brain tissue microstructure estimation.

Inspired by the advances in computational neuroscience for modelling brain cells, and the growing availability of public databases of digitalised brain cell microstructure with increasing quality year-on-year, we developed a toolbox to perform numerical simulation of molecular diffusion within realistic digitalised brain cells.

Methods

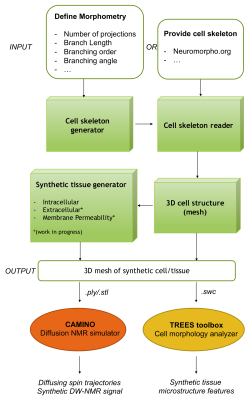
The proposed toolbox (Fig.1, green blocks) is implemented in MATLAB and designed to optimally interface with CAMINO¹ for the synthetic DW-NMR signal computation, and with standard toolboxes to visualize and analyse neuronal trees, like TREES². A block-diagram of the proposed framework is shown in Fig.1.

Here we address two main challenges in performing numerical simulation of diffusion process within realistic three-dimensional digital representation of cell/tissue:

1) Handling the large complexity of such systems, which requires an optimised digital representation that minimises computational burden;

2) Ensuring correct connectivity between the distinct compartments comprising the system (like each branch of a dendritic tree, cellular projections and soma, different cellular entities, extra-cellular space, etc.).

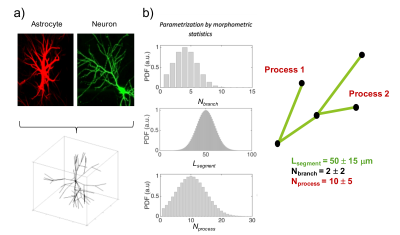
Modelling cell structure and complexity. To model complex cell structures with correct connectivity, we describe each cellular compartment as a branched structure (backbone), whose individual branch has a specific size (radius) and each process (collection of branches sharing the same parent) radiates from the cell body (soma) having itself a specific radius (Fig.2-a). The ensemble of backbone and sizes defines our cellular skeleton. The skeleton of digital cells can be either imported into the proposed toolbox from available public databases, like NeruoMorpho³, or generated using a statistical model that parametrizes the complex and heterogeneous morphology of brain cells with a small set of morphometric statistics⁴ (Fig.2-b). The latter allows one to define the morphometric statistics a priori and thus to investigate different cellular/tissue scenarios/conditions in a controlled fashion.

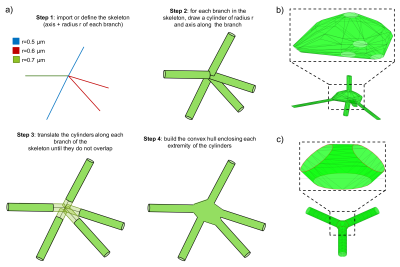
Modelling cell body and branching point. Once a cellular skeleton is provided (imported or generated), the toolbox generates a 3D mesh of the whole structure, taking into account individual branch and soma size. We use an efficient algorithm to ensure that the 3D mesh has smooth transition at critical points that connect different branches and the soma (Fig.3). The toolbox outputs the 3D mesh in standard file formats, including PLY, STL and SWC.

Simulating diffusion process. With the support for the PLY format, which is compatible with CAMINO¹, the toolbox enables DW-NMR signal synthesis with one of the most popular diffusion simulators.

Analysing cell morphology. With the support for the SWC file format, which is widely used in bioinformatics to store/share information on complex cell structures, the toolbox provides a compatible file format to be used with the TREES toolbox². This allows an accurate investigation of the relationship between the simulated DW-NMR signal and the synthetic cell microstructure.

Results

Fig.4 reports some examples of the proposed pipeline applied to increasingly complex cellular configurations. In this demonstration, the skeleton was defined by choosing different parameters for the morphometric statistics.

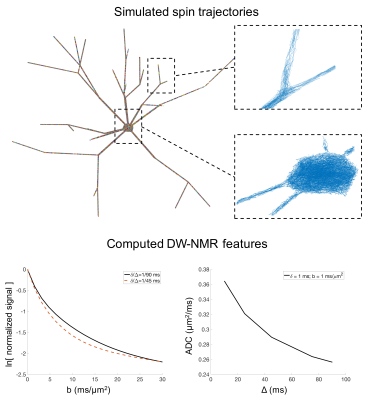
Fig.5 presents an example of spin particles trajectories within a synthetic 3D cell geometry and the corresponding DW-NMR signals (normalized signal b value dependence and apparent diffusion coefficient time dependence). This illustrates the possible sequence/experimental conditions that the toolbox can help investigate.

Discussion and Conclusion

Acknowledgements

References

¹ Cook P A, Bai Y, Nedjati-Gilani S K K S, Seunarine K K, Hall M G, Parker G J, Alexander D C. Camino: open-source diffusion-MRI reconstruction and processing. In 14th scientific meeting of the international society for magnetic resonance in medicine 2004 (Vol. 2759). Seattle WA, USA.

² Cuntz H, Forstner F, Borst A, Häusser M. One rule to grow them all: A general theory of neuronal branching and its practical application. PLoS Computational Biology 2010; 6(8): e1000877.

³ http://neuromorpho.org

⁴ Palombo M, et al. New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. PNAS 2016; 113(24): 6671-6676.

⁵ Szafer et al, Theoretical Model for Water Diffusion in Tissues. MRM 1995; 33:697-712

⁶ Ford and Hackney, Numerical Model for Calculation of Apparent Diffusion Coefficients (ADC) in Permeable Cylinders-Comparison with Measured ADC in Spinal Cord White Matter. MRM 1997; 37:387-94.

⁷ Liu et al. Characterizing Non-Gaussian Diffusion by Using Generalized Diffusion Tensors. MRM 2004; 51:924-37.

⁸ Peled. New Perspectives on the Sources of White Matter DTI Signal. IEEE TMI 2007; 26:1448-55.

⁹ Balls et al. A Simulation Environment for Diffusion Weighted MR Experiments in Complex Media. MRM 2009; 62:771-8.

¹⁰ Nilsson et al. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR Biomed 2012; 25:795-805.

¹¹ Fieremans et al. Monte Carlo study of a two-compartment exchange model of diffusion. NMR Biomed 2010; 23:711-24.

¹² Landman et al. Complex geometric models of diffusion and relaxation in healthy and damaged white matter, NMR Biomed 2010; 23:152-62.

¹³ Yeh et al. Diffusion Microscopist Simulator: A General Monte Carlo Simulation System for Diffusion Magnetic Resonance Imaging, PLoS One 2013; e76626.