Synopsis

Well characterized phantoms are essential for time-dependent diffusion model validations. Here we introduce a phantom made of permeable barriers with highly tunable micro-structural characteristics such as pore size, pore density and permeability and perform time-dependent diffusion measurements using three NMR and MRI systems. Our experimental results agree with the theory of time-dependent diffusion in disordered systems, making the phantom suitable for model validations in clinical and preclinical systems.

Introduction

Methods

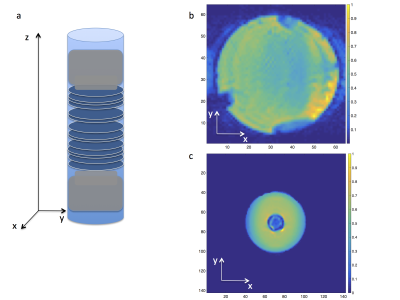
Phantom: Porous films (Sterlitech-CO) made of polycarbonate were used to create a permeable phantom. The films were circular with a diameter of 27$$$mm$$$, 6$$$\,\mu\,m$$$ thick, had pores $$$0.15\,\mu\,m$$$ in diameter and a density of 5 pores/$$$\mu\,m^2$$$. A cylindrical tube was designed to hold the films together (Fig.1a), with two pistons on either side of the cylinder for controlling the distance between the films. The phantom was constructed by stacking 90 films along $$$z$$$ with an average distance between them $$$\bar{a}=30\,\mu\,m$$$, then filled with water, sonicated and depressurized for microbubble removal before performing MR experiments. In addition, the tube was embedded in a larger cylinder filled with water to enhance the signal when scanning on the Siemens-Prisma (Fig.1c). Note that for the NMR experiments $$$\bar{a}=12\mu\,m$$$.

MR experiments were performed on three systems: a preclinical imaging system (7T Bruker-Biospec), a clinical system (3T Siemens-Prisma) and an NMR system (4.2T TecMag-Apollo). For the diffusion measurements a STEAM sequence was used. Below are the experimental parameters for each system. Biospec: number of directions$$$\,=\,124$$$, $$$b=0.2,\,0.6,\,1.0,\,1.5,\,2.0\,ms/\mu\,m^2$$$, $$$\Delta=11-3000\,ms$$$, $$$\delta$$$=2.1$$$\,ms$$$, TE=19$$$\,ms$$$, TR=6$$$\,s$$$, Res=0.5x0.5x2.0$$$\,mm^3$$$. Prisma: number of directions$$$\,=\,124$$$, $$$b=\,0.5,\,1.0,\,1.2,\,1.5\,ms/\mu\,m^2$$$, $$$\Delta=40-1900\,ms$$$, $$$\delta$$$=10$$$\,ms$$$, TE=93$$$\,ms$$$, TR=8$$$\,s$$$, Res=2.0x2.0x1.5$$$\,mm^3$$$. Apollo: $$$b=\,0.1,\,0.13,\,0.17,\,0.22,\,0.26,\,0.32\,ms/\mu\,m^2$$$, $$$\Delta=1.6-3500\,ms$$$, $$$\delta$$$=120$$$\,\mu\,s$$$, TE=15$$$\,\mu\,s$$$, TR=10$$$\,s$$$. The diffusion images were denoised⁷ and the signal was averaged within the ROI followed by a DKI^8,9 (Diffusion Kurtosis Imaging) weighted linear least squares fit. For the NMR experiments, the b-value was chosen such that $$$bD_0<1$$$ to avoid higher order cumulants and a least squares fit was performed to obtain the diffusivity¹⁰. Additional NMR experiments were performed on the setup of reference¹⁰ using phantoms of varying pore size from $$$0.15-0.65\,\mu\,m$$$.

Theory

The presence of microstructure in complex media manifests itself as power-law tail in the time-dependent diffusion coefficient¹¹

$$D(t)\simeq\,D_\infty+c\,t^{-\vartheta},\quad(1)$$

for times $$$t>>\tau_r$$$ much exceeding the residence time $$$\tau_r\equiv\bar{a}/2\kappa$$$ between adjacent membranes, where $$$\kappa$$$ is the membrane permeability, and $$$D_{\infty}$$$ is the diffusivity at $$$t\rightarrow\infty$$$.

In the case of short-range disorder (similar to Poissonian disorder), the exponent $$$\vartheta=1/2$$$ in Eq.(1). Here, we experimentally estimate the permeability of our membranes using¹¹,

$$\kappa = \frac{D_0}{\bar{a}\zeta}\,,\quad\zeta=\frac{D_0}{D_{\infty}} - 1,\quad(2)$$

and show the validity of scaling (1).

Results/Discussion

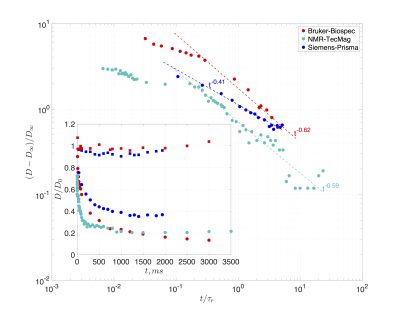
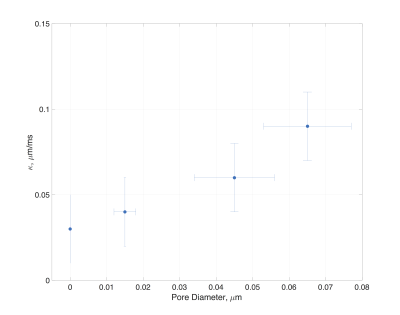
Fig. 2 shows the diffusivity time dependence in the phantom along ($$$z$$$) and transverse ($$$x-y$$$) to the porous films. The inset of Fig. 2 highlights the diffusivities normalized with $$$D_0$$$ at the experimental temperature. A characteristic time-dependence was observed along the $$$z$$$ direction whereas in directions $$$x-y$$$, the diffusivity had no time-dependence. Since the permeable films were placed in random positions along the cylindrical tube (Fig. 1a), a time-dependence according to Eq.(1) is expected for the diffusivity. Indeed, by performing a three degrees of freedom least squares fit, and normalizing with $$$D_{\infty}$$$, a power law of $$$\vartheta=0.62$$$, $$$\vartheta=0.41$$$ and $$$\vartheta=0.59$$$ was observed, in agreement with Eq.(1). The permeability of the phantom can be estimated from Eq.(2) using the $$$D_0$$$ at the experimental temperature and $$$D_{\infty}$$$ from the fit. For the NMR system $$$\kappa\simeq\,0.04\,\mu\,m/ms$$$ whereas for Biospec and Prisma MRI systems $$$\kappa\simeq\,0.03\,\mu\,m/ms$$$ and $$$\kappa\simeq\,0.025\,\mu\,m/ms$$$ respectively. Fig. 3 shows the permeability-values of phantoms made with films of different pore size.

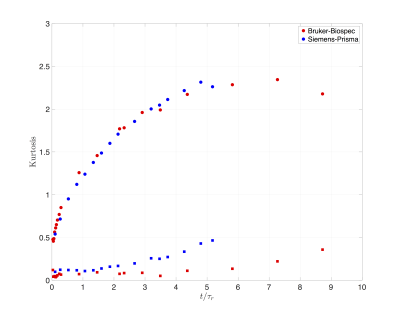
Fig. 4 shows the time dependence of the kurtosis for the scans performed on the MRI systems. Kurtosis along the $$$z$$$ direction showed a non-monotonic time-dependence, similar to what was observed in the brain¹², and peaks at approximately 6$$$\tau_r$$$.

Conclusions

Acknowledgements

References

1. Komlosh, M. E., et al. "Anisotropic phantom to calibrate high-q diffusion MRI methods." Journal of Magnetic Resonance 275 (2017): 19-28.

2. Lemberskiy, Gregory, et al. "Validation of surface‐to‐volume ratio measurements derived from oscillating gradient spin echo on a clinical scanner using anisotropic fiber phantoms." NMR in Biomedicine 30.5 (2017).

3. Fillard, Pierre, et al. "Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom." Neuroimage 56.1 (2011): 220-234.

4. Komlosh, Michal E., et al. "Pore diameter mapping using double pulsed-field gradient MRI and its validation using a novel glass capillary array phantom." Journal of magnetic resonance 208.1 (2011): 128-135.

5. Fieremans, Els, et al. "Simulation and experimental verification of the diffusion in an anisotropic fiber phantom." Journal of Magnetic Resonance 190.2 (2008): 189-199.

6. Burcaw, Lauren M., Els Fieremans, and Dmitry S. Novikov. "Mesoscopic structure of neuronal tracts from time-dependent diffusion." NeuroImage 114 (2015): 18-37.

7. Veraart, Jelle, et al. "Denoising of diffusion MRI using random matrix theory." NeuroImage 142 (2016): 394-406.

8. Veraart, Jelle, et al. "Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls." NeuroImage 81 (2013): 335-346.

9. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., & Kaczynski, K. (2005). Diffusional kurtosis imaging: The quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 53(6), 1432-1440.

10. Papaioannou, A., Novikov, D. S., Fieremans, E., & Boutis, G. S. (2016). Diffusion distinguishes between structural universality classes of disordered media. arXiv preprint arXiv:1607.08639.

11. Novikov, D. S., Jensen, J. H., Helpern, J. A., & Fieremans, E. (2014). Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences, 111(14), 5088-5093.

12. Pyatigorskaya, N., Bihan, D., Reynaud, O., & Ciobanu, L. (2014). Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 tesla in the healthy rat brain cortex. Magnetic resonance in medicine, 72(2), 492-500.