0694

Bayesian Deep Learning for Uncertainty Generation in MR Image Segmentation
Gengyan Zhao1, Fang Liu2, Mary E. Meyerand1,3, and Rasmus M. Birn1,4

1Department of Medical Physics, University of Wisconsin - Madison, Madison, WI, United States, 2Department of Radiology, University of Wisconsin - Madison, Madison, WI, United States, 3Department of Biomedical Engineering, University of Wisconsin - Madison, Madison, WI, United States, 4Department of Psychiatry, University of Wisconsin - Madison, Madison, WI, United States

Synopsis

The ability of generating model uncertainty for a predictive system on each prediction is crucial for decision-making, especially in the field of medicine, but it has been a missing part in conventional deep learning models. We propose the utilization of Bayesian deep learning, which combines Monte Carlo dropout layers with the original deep neural network at testing time to enable model uncertainty generation. Its prediction accuracy and the behavior of uncertainty were studied on MRI brain extraction. Its segmentation accuracy outperforms 6 popular methods, and the uncertainty’s reactions to different training set sizes and inconsistent training labels meet the expectation well.

Introduction

Deep learning based neural networks have been successfully applied to MR image segmentation with outstanding accuracy1. In addition to high accuracy, the model uncertainty on each prediction is also crucial for well-informed decision-making and artificial intelligence safety in a mature predictive system2, especially in the field of medicine where ground truth is not available in real prediction practice, and decision correctness is vital3,4. However, conventional deep learning models do not provide model uncertainty, and the probabilities generated at the end of the pipeline are often mistakenly taken as the model confidence5. Recently, the progress on combining probability theory and Bayesian modelling with deep learning showed its potential on modelling uncertainty in computer vision6. In this study, we propose to utilize the framework of Bayesian deep learning to generate model uncertainty in MR image segmentation. Its performance on segmentation accuracy and the behavior of the generated model uncertainty are also demonstrated.

Methods

In addition to predicting the probability for each input in each label category, Bayesian deep learning can also generate model uncertainty on each prediction. This is achieved by involving Monte Carlo dropout layers into the network at testing time6.$$\begin{align}&p({{y}^{\text{*}}}|{{x}^{\text{*}}},X,Y)\approx\int{p({{y}^{\text{*}}}|{{x}^{\text{*}}},W)q(W)dW}\approx\frac{1}{T}\underset{t=1}{\overset{T}{\mathop\sum}}\,p({{y}^{\text{*}}}|{{x}^{\text{*}}},{{{\hat{W}}}{t}})\\&{{{\hat{W}}}_{t}}\text{ }\!\!~\!\!\text{ }\tilde{\ }\text{ }\!\!~\!\!\text{ }q(W) \\\end{align}$$To predict the label $$${{y}^{*}}$$$ for the input $$${{x}^{*}}$$$ with the training inputs $$$X$$$ and corresponding labels $$$Y$$$, the integral in the equation can be approximated with Monte Carlo integration, which is identical to Monte Carlo dropout sampling of the Bayesian neural network during testing. This can be considered as sampling the posterior distribution over the weights to get the posterior distribution of the predicted label probabilities. $$$T$$$ is the total number of samples, and $$${{\hat{W}}_{t}}$$$ is the set of weights during $$$t$$$th dropout sampling. The mean of these samples is used as the prediction of the probability map for each label, while the standard deviation of them is used as the model uncertainty on each prediction6. In this study, Monte Carlo dropout layers were combined with deep convolutional encoder-decoder network to form a Bayesian neural network7, and it was applied on the brain extraction of MR images (Figure 1). Its performance was compared with six popular brain extraction methods with different metrics. The effect of Monte Carlo sample size on segmentation accuracy and the behavior of the prediction uncertainty against training set size and the training label consistency were also studied. The evaluation was done in a 2-fold cross validation manner, with a manually brain-extracted dataset comprising 100 rhesus macaque T1w brain volumes, which were collected in a 3T MRI scanner (MR750, GE Healthcare, Waukesha, USA).

Results

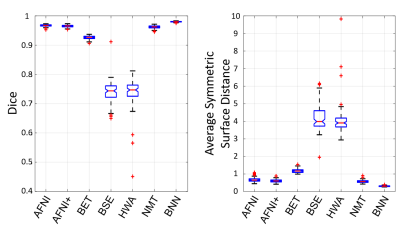
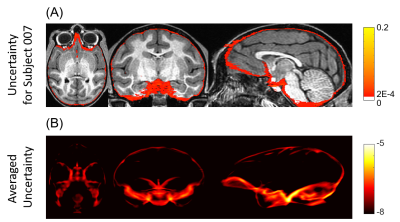
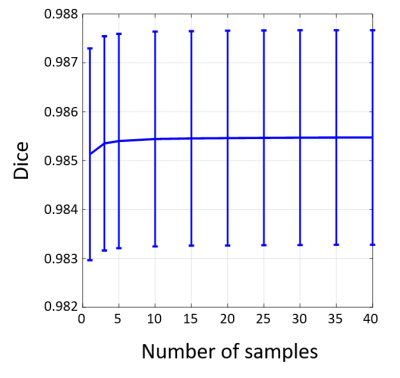
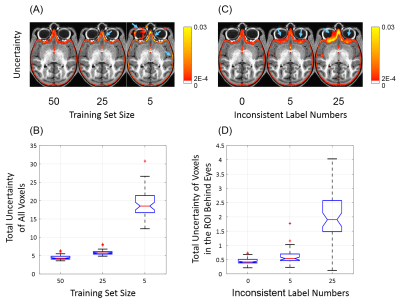
Bayesian convolutional encoder-decoder network outperforms six popular publicly available brain extraction methods with a mean Dice coefficient of 0.985 and a mean average symmetric surface distance of 0.220 mm (Figure 2), and a better performance against all the compared methods was verified by statistical tests (all Bonferroni corrected p-values<10-4). With an optimized GPU implementation, the prediction time of the whole pipeline is around 40 seconds. Figure 3(A) shows the voxel-labeling uncertainty on a representative subject. The uncertainty map of each subject was also transformed, averaged and displayed in the template space in Figure 3(B), which illustrates the systematic uncertainty distribution of the proposed method on the dataset. Overall, the uncertainty of the brain extraction is very low, and the relative high uncertainty region is at boundary of the brain. Figure 4 shows that there is no obvious improvement on segmentation accuracy beyond 5 samples in dropout sampling. Figure 5 shows that as the training set size decreases, or the number of inconsistent labels increases, the uncertainty of each subject tends to increase and deviate more from the sample mean.

Discussion

Being different from traditional deep learning based neural networks, Bayesian neural network is a kind of probabilistic neural network, which can provide the model uncertainty on each prediction as well as make accurate prediction for each input. As is known, even well-trained neural networks cannot be accurate on every situation, and the decision to accept a prediction or reject it and start human intervention relies on the model uncertainty for each specific case. The results in this study show that the uncertainty information offered by Bayesian deep learning fulfills this requirement well.

Conclusion

In this study, we propose the utilization of Bayesian deep learning in MR image segmentation, and illustrate its ability to generate model uncertainty on each prediction for decision-making as well as make accurate predictions. The novel Bayesian deep learning framework also accurately reflected the expected behaviors of model uncertainty related to training set size and training label consistency.

Acknowledgements

The authors gratefully acknowledge the contribution of Dr. Jonathan A. Oler, Dr. Ned H. Kalin, Ms. Maria Jesson and Dr. Andrew Fox (UC-Davis), and the assistance of the staffs at the Harlow Center for Biological Psychology, the Lane Neuroimaging Laboratory at the Health Emotions Research Institute, Waisman Laboratory for Brain Imaging and Behavior, and the Wisconsin National Primate Research Center. This work was supported by grants from the National Institutes of Health: P51-OD011106; R01-MH046729; R01-MH081884; P50-MH100031. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

References

1. Wachinger, C., Reuter, M. & Klein, T. DeepNAT: Deep convolutional neural network for segmenting neuroanatomy. NeuroImage (2017). doi:10.1016/j.neuroimage.2017.02.035

2. Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 521, 452–459 (2015).

3. Haskins, R., Osmotherly, P. G., Tuyl, F. & Rivett, D. A. Uncertainty in clinical prediction rules: the value of credible intervals. J. Orthop. Sports Phys. Ther. 44, 85–91 (2014).

4. Duggan, C. & Jones, R. Managing uncertainty in the clinical prediction of risk of harm: Bringing a Bayesian approach to forensic mental health. Crim. Behav. Ment. Health CBMH 27, 1–7 (2017).

5. Gal, Y. & Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. in PMLR 1050–1059 (2016).

6. Gal, Y. & Ghahramani, Z. Bayesian Convolutional Neural Networks with Bernoulli Approximate Variational Inference. ArXiv150602158 Cs Stat (2015).

7. Kendall, A., Badrinarayanan, V. & Cipolla, R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding. ArXiv151102680 Cs (2015).

Figures

Figure1. Illustration of involving Monte Carlo dropout layers into a convolutional encoder-decoder network to make it a Bayesian neural network. Both Monte Carlo dropout training and dropout testing can be carried out by the same group of dropout layers. During the dropout testing for each subject, the mean of the dropout samples of the probabilities in the softmax layer are used to predict the segmentation masks, and the standard deviation of them are used as the model uncertainty for each class.

Figure 2. Evaluation scores in boxplots from different brain extraction methods. In the figure points are drawn as outliers with red ‘+’ symbols, if they are greater than q3+1.5(q3-q1) or less than q1-1.5(q3-q1), where q1 and q3 are the first and third quartiles respectively. AFNI: 3dSkullStrip in AFNI; AFNI+: 3dSkullStrip in AFNI with redused coronal slice thickness to one half of the original value; BET: Brain Extraction Tool; BSE: Brain Surface Extractor; HWA: Hybrid Watershed Algorithm; NMT: National Institute of Mental Health Macaque Template; BNN: Bayesian Neural Network.

Figure 3. Uncertainty maps generated by Monte Carlo dropout testing. (A) The uncertainty map generated for a representative subject, subject 007. (B) The averaged uncertainty map across all the 100 subjects in the template space. For display purposes, the natural logarithm of the averaged uncertainty map collapsed (averaged) along each axis is shown.

Figure 4. Brain extraction accuracy against the number of Monte Carlo dropout samples in the Bayesian neural network. A subset of 30 subjects was used to study how the number of Monte Carlo samples in dropout testing affects the final segmentation accuracy. The averaged Dice coefficient over 30 subjects with standard deviation error bar is plotted at each dropout sample size.

Figure 5. Effects of training set size and training label consistency on the output uncertainty. (A) Uncertainty maps on subject 007 generated by Bayesian neural network trained with different training set sizes. (B) Total uncertainty of all the voxels in the 3D brain volume of each subject in the 50 subjects generated by Bayesian neural network trained with different training set sizes. (C) Uncertainty maps on subject 007 generated by Bayesian neural network trained with 50 subjects in which different numbers of manual labels were replaced by inconsistent labels. (D) Total uncertainty of the voxels in the ROI behind the eyes of each subject in the 50 subjects generated by Bayesian neural network trained with 50 subjects in which different numbers of manual labels were replaced by inconsistent labels. The inconsistent labels in (C) and (D) were generated by AFNI+, and mismatch the corresponding manual labels in regions behind the eyes. In the figures, points are drawn as outliers with red ‘+’ symbols, if they are greater than q3+1.5(q3-q1) or less than q1-1.5(q3-q1), where q1 and q3 are the first and third quartiles respectively.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0694