Synopsis

The Cramer-Rao bound (CRB) based experiment design was previously described to optimize the SNR efficiency of MRF experiments. Here we revisit such a problem and provide new insights. Specifically, we present a new CRB-based experiment design approach, which introduces an additional set of constraints on the variation of flip angles to enforce the smoothness of the magnetization evolution. We demonstrate that the proposed approach is advantageous for highly-undersampled MRF experiments. We evaluated the effectiveness of the proposed approach with both simulations and phantom experiments.

Introduction

Theory

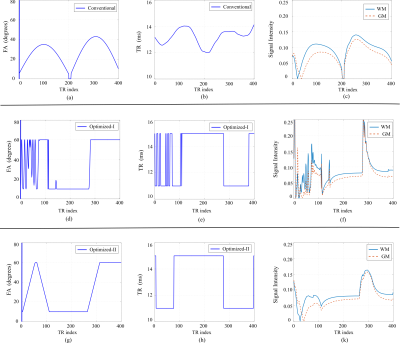
Given that the CRB provides a lower bound on the smallest possible variance for any unbiased estimator, it can be used to characterize the SNR efficiency of an MRF experiment. Denote the unknown tissue parameters as $$$\theta=[T_1,T_2, M_0]$$$, and $$$\mathbf{C}(\theta)$$$ as the CRB matrix associated with an MRF experiment. The previous work^{3, 4, 5} (referred as Optimized-I) formulates the following experiment design problem, which optimizes the schedule of flip angles and repetition times: $$\underset{\alpha_n,~TR_n}{\mathrm{min}} \sum_{i=1}^L\sum_{i=1}^3\omega_i \sqrt{[\mathbf{C}(\theta^{(l)})]_{ii}}/\theta^{(l)}_i,\\\mathrm{s.t.} ~~~\alpha_n^{\mathrm{min}} \leq\alpha_n\leq\alpha^{\mathrm{max}}_n,\\~~~~~~~~~~~~TR_n^{\mathrm{min}} \leq TR_n\leq TR^{\mathrm{max}}_n.$$ Here the weighting $$$\omega_i$$$ is the weighting parameter that balances the importance of different tissue parameters. In this work, we introduce a set of new constraints into the experiment design, which restricts the flip angle variations. Accordingly, we reformulate the following experiment design problem (referred as Optimized-II): $$\underset{\alpha_n,~TR_n}{\mathrm{min}} \sum_{i=1}^L\sum_{i=1}^3\omega_i \sqrt{[\mathbf{C}(\theta^{(l)})]_{ii}}/\theta^{(l)}_i,\\\mathrm{s.t.} ~~~\alpha_n^{\mathrm{min}} \leq\alpha_n\leq\alpha^{\mathrm{max}}_n,\\~~~~~~~~~~~~ \mid \alpha_{n+1}-\alpha_{n}\mid\leq \triangle \alpha^{\mathrm{max}}\\~~~~~~~~~~~~TR_n^{\mathrm{min}} \leq TR_n\leq TR^{\mathrm{max}}_n.$$ To illustrate the role the new constraints, we show the optimized acquisition parameters, as well as resulting magnetization evolution, in Figure 1. As can be seen, the oscillation behavior of magnetization evolution has been effectively suppressed with the new constraints, resulting in smooth magnetization evolution. The smooth magnetization evolution is advantageous for reconstruction with highly-undersampled MRF experiments. More specifically, for the conventional approach¹ that utilizes direct pattern matching, smooth magnetization evolution can be better differentiated from aliasing artifacts, leading to improved pattern matching performance. For the low-rank/subspace reconstruction^{6, 7, 8}, smooth magnetization evolution often results in lower low-rank modeling error. For other reconstruction approaches^{9, 10} that requires solving a nonlinear and non-convex optimization problem, a good initialization from the conventional approach or low-rank reconstruction also leads to better reconstruction performance.

Methods and Results

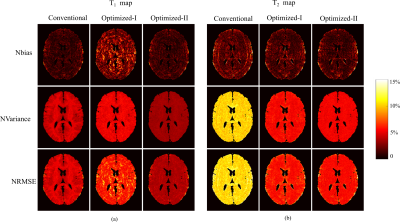
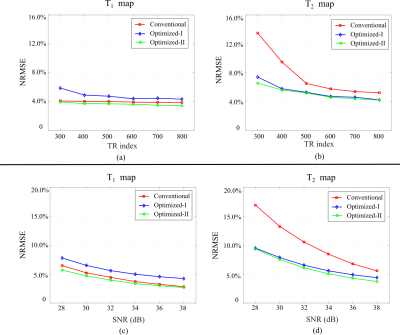
We first performed numerical simulations to evaluate the proposed approach. We simulated FISP-MRF experiments² on a brain phantom created from the BrainWeb¹¹ database. We simulated highly-undersampled experiments using the acquisition parameters from the conventional MRF, Optimized-I, and Optimized-II, and applied the ML approach to reconstruct MR tissue parameter maps. Figure 2 shows the reconstruction results for N = 400. As can be seen, with the new constraint, Optimized-II outperforms the conventional MRF and Optimized-I for both T₁ and T₂ maps. This clearly demonstrates the merit of the proposed experiment design. Figure 3 evaluates the bias, variance, mean-squared error of the reconstructed parameter maps. As can be seen, Optimized-II significantly reduces the bias of parameter estimation with smooth magnetization evolutions. Figure 4 show the reconstruction results from highly-undersampled MRF experiments at different SNR levels as well as different acquisition lengths. Again, Optimized-II consistently improves over the conventional MRF and Optimized-II.

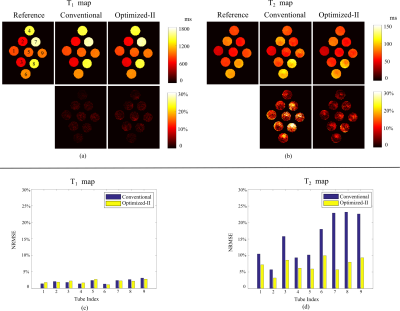
Finally, we evaluated the proposed approach with the phantom experiments. Specifically, we scanned a physical phantom with 9 tubes on a 3T Siemens scanner equipped with 32 coils. Here each tube has different combinations of T₁ and T₂ values. The relevant imaging parameters include: FOV = 300×300 mm², matrix size = 256×256, and slice thickness = 5 mm. Here we acquired a set of fully-sampled MRF experiment as reference. Given the optimized-II improves Optimized-I, here we only compared with the conventional MRF. Figure 4 shows the reconstructed T₁ and T₂ maps and Figure 5 shows the reconstruction error with respect to each tube. Consistent with the numerical simulations, Optimized-II improves over the conventional MRF experiments.

Conclusion and Discussion

This work described a new CRB-based experiment design, which encodes MR tissue parameters with maximal SNR efficiency, while taking into account the constraints from the image reconstruction process. The proposed approach improves performance for highly-undersampled MRF experiments.

As an interesting observations, the optimized acquisition parameters appear to be highly structured rather than randomly-varying/pseudo-randomly varying as described in the conventional MRF experiments^1,2. Early work has shown that certain CRB based experiment design problem can be casted as optimal control problems¹². It is possible that our observations could be explained by the principles from optimal control theory. This motivates an in-depth theoretical study in the future research.

Acknowledgements

References

[1] D. Ma, V. Gulanni, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, pp. 187-192, 2013.

[2] Y. Jiang, D. Ma, N. Seiberlich, V. Gulani, and M. A. Griswold, “MR fingerprinting using fast imaging with steady state precession (FISP) spiral readout,” Magn. Reson. Med., vol. 74, pp. 1621-1631, 2015.

[3] B. Zhao, J. P. Haldar, K. Setsompop, and L. L. Wald, “Towards optimized experiment design for magnetic resonance fingerprinting”, in Proc. Int. Symp. Magn. Reson. Med., p. 2835, 2016.

[4] B. Zhao, J. P. Haldar, K. Setsompop, and L. L. Wald, “Optimal experiment design for magnetic resonance fingerprinting”, in Proc. IEEE Eng. Med. Bio. Conf. pp. 453-456, 2016.

[5] J. Asslander, D. Sodickson, R. Lattanzi, and M. Cloos, “Relaxation in polar coordinates: Analysis and optimization of MR fingerprinting”, in Proc. Int. Symp. Magn. Reson. Med., p. 217, 2017.

[6] B. Zhao, “Model-Based iterative reconstruction for magnetic resonance fingerprinting”, In Proc. IEEE Int. Conf. Image Process. pp. 3392-3396, 2015.

[7] B. Zhao, K. Setsompop, E. Adalsteinsson, B. Gagoski, H. Ye, D. Ma, Y. Jiang, P. Ellen Grant, M. A. Griswold, and L. L. Wald, “Improved magnetic resonance fingerprinting with low-rank and subspace modeling”, Magn. Reson. Med., 2017. In press.

[8] J. Asslander, M. Cloos, F. Knoll, D. Sodickson, J. Hennig, and R. Lattanzi, “Low rank alternating direction method of multipliers reconstruction for MR fingerprinting”, Magn. Reson. Med., 2017. In press.

[9] M. Davies, G. Puy, P. Vandergheynst, Y. Wiaux, “A compressed sensing framework for magnetic resonance fingerprinting”, SIAM Imaging Science, pp. 2623-2656, 2014.

[10] B. Zhao, K. Setsompop, H. Ye, S. F. Cauley, and L. L. Wald, “Maximum likelihood reconstruction for magnetic resonance fingerprinting”, IEEE Transactions on Medical Imaging, vol. 35, pp. 1812-1823, 2016.

[11] D. L. Collins, A. P. Zijdenbos, V. Kollokian, J. G. Sled, N. J. Kabani, C. J. Holmes, and A. C. Evans, “Design and construction of a realistic digital brain phantom, IEEE Trans. Medical Imaging, vol. 17, pp. 463-468.

[12] J. Maidens, A. Packard, and M. Arcak, “Parallel dynamic programming for optimal experiment design in nonlinear systems”, 55th IEEE Conf. on Decision and Control, pp. 2894-2899, 2016.