0665
Tract-Based Cluster Analysis1Natbrainlab, Forensic and Neurodevelopmental Science, King's College London, London, United Kingdom, 2Department of Neuroimaging, King's College London, London, United Kingdom, 3Department of Psychology, King's College London, London, United Kingdom, 4The Sackler Institute for Translational Neurodevelopment, King's College London, London, United Kingdom
Synopsis
The use of a-priori anatomical information can effectively improve statistical analysis of neuroimaging data. In this work, we introduce a new method called Tract-Based Cluster Analysis (TBCA) that exploits the rich anatomical information present in a whole-brain tractogram to inform the cluster-level inference analysis of voxel-based images. The method is based on the novel concept of hyper-voxel which incorporates local and global anatomical information derived from tractography data. When applied to real clinical data TBCA demonstrates clear benefits compared to previous cluster-level inference approaches.
Introduction
Cluster-level inference remains one of the most popular methods for the analysis of neuroimaging data. The basic premise relies on the assumption that statistical differences detected within regions of contiguous voxels should better reflect the presence of true biological effects in the images than single voxels. When implemented using permutation tests1, cluster-level inference is well known for effectively dealing with multiple comparisons and therefore increasing the sensitivity of the statistical analysis2. However, one of its drawbacks is a low anatomical specificity. When significant results are expected to follow brain structures, it is reasonable to introduce additional hypothesis about how the resulting clusters should match the underlying anatomy. For example, voxels belonging to the same white-matter tract should be detected within common clusters, while voxels from distinct and unrelated anatomical areas should not. To achieve this, we have developed a new method called Tract-Based Cluster Analysis (TBCA) that uses the anatomical properties of white-matter tracts both at the local and global scale to improve the cluster-level inference of voxel-based brain images. Here, we provide a description of the method and the results of its application to find group differences in Motor Neuron Disease (MND) where degeneration of specific tracts is well stablished.
Methods
Theory
TBCA is carried out in a higher dimensional space in which hyper-voxels are generated to encode additional anatomical parameters. These parameters are obtained from tractography data and represent local and global anatomical properties of the tracts intersecting each voxel. Given a tractography dataset, all the corresponding hyper-voxels are computed in order to create a hyper-voxel template that encapsulates both local and global anatomical information at the level of each voxel. Any voxel-based data can be then projected onto the hyper-voxel template for further analysis using the anatomical information available now at each hyper-voxel. Specifically, TBCA applies non-parametric cluster-inference to clusters of hyper-voxels computed using novel anatomically-informed clustering criteria that reflects the anatomical information encoded in the tractogram. For this purpose, we have implemented a new TBCA toolbox which is also compatible with SnPM3. A summary of the TBCA pipeline is shown in Figure-1.
Hyper-voxel encoding
For each tract intersecting a brain voxel at position $$$\mathit{\mathbf{p}}$$$, we can encode the local orientation of the tract as a vector $$$\mathit{\mathbf{v}}$$$ and the relative position of the voxel respect to a global descriptor of the entire trajectory of the tract $$$\mathit{\mathbf{q}}$$$. By using a multidimensional matrix to extends the original voxel-space, these three parameters can be discretised in the form of a hyper-voxel determined by coordinates $$$\mathit{\mathbf{hv}}=\mathit{\mathbf{(p,v,q)}}$$$. For a given tract represented by an ordered list of point coordinates $$$\mathit{\mathbf{\{p_i}\}}$$$, the corresponding hyper-voxel representation is equivalent to the list of discretised coordinates $$$\mathit{\mathbf{hv}_i}=\{\mathit{\mathbf{p_i}},\mathit{\mathbf{v_i}},\mathit{\mathbf{q_i}}\}$$$. A hyper-voxel template is the hyper-voxel representation of all tracts in a given tractography template.
Hyper-voxel anatomically-informed clustering criteria
As shown in Figure-2, two hyper-voxels $$$\mathit{\mathbf{hv}_1}=\{\mathit{\mathbf{p_1}},\mathit{\mathbf{v_1}},\mathit{\mathbf{q_1}}\}$$$ and $$$\mathit{\mathbf{hv}_2}=\{\mathit{\mathbf{p_2}},\mathit{\mathbf{v_2}},\mathit{\mathbf{q_2}}\}$$$ belong to the same cluster if:
- They are connected by a tract according to the hyper-voxel template, or
- They are adjacent as voxels and have both equivalent local orientations $$$\mathit{\mathbf{v_1≈v_2}}$$$ and global tract-parameter values $$$\mathit{\mathbf{q_1≈q_2}}$$$.
Application to MND
To assess the performance of TBCA compared with classical cluster-level inference, we investigated group differences between a group of MND patients (n=23) and paired controls (n=24), using co-registered fractional anisotropy (FA) maps. We used SnPM for voxel-level inference including age and gender as covariates. Then, we separately run cluster-level inference on the resulting statistic maps with SnPM3 and TBCA using a cluster-forming threshold of p=0.01. For TBCA, we used a hyper-voxel template based on an average of twenty randomly selected HCP4 whole-brain tractograms normalised to MNI1525 template.
Results
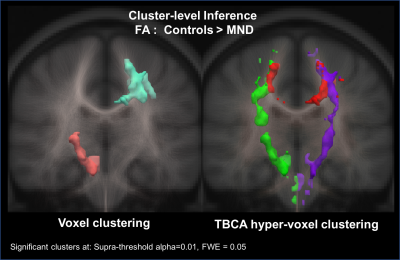
Figure-3 shows the results of the cluster analysis obtained with SnPM and TBCA in MND. Compared to standard cluster inference, TBCA detected more and larger clusters: bilaterally, almost complete branches of the cortico-spinal tract are visible in TBCA as two distinct significant clusters. An additional and anatomically distinct cluster along the midsegment of the body of the corpus callosum connecting motor regions is also evident. The clusters identified by TBCA are along tracts where biologically changes are known to occur due to neurodegeneration. In comparison, SnPM detects only two smaller clusters, one emerging as a partial mix of distinct intersecting white-matter tracts.
Conclusions
Tractography can provide valuable a-priori anatomical information to improve statistical analysis in neuroimaging. The use of hyper-voxels increases the sensitive of cluster inference analysis and also provides the anatomical specificity required to disentangle distinct clusters belonging to different anatomical tracts. Here we have demonstrated its application to a diffusion imaging dataset but in principle any imaging modality based on quantitative maps (i.e. relaxometry, PET, etc) will benefit from TBCA.
Acknowledgements
This work is funded by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy's and St Thomas' NHS Foundation Trust and King's College London. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.
Data were provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Marco Catani is the recipient of the Wellcome Trust Investigator Award No. 103759/Z/14/Z. The study was supported by the Wellcome Trust (Grant reference 083477/Z/07/Z).
References
1. Bullmore, E.T. et al., 1999. Global, voxel, and cluster tests, by theory and permutation, for a difference between two groups of structural mr images of the brain. IEEE Transactions on Medical Imaging, 18(1), pp.32–42.
2. Eklund, A., Nichols, T.E. & Knutsson, H., 2016. Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proceedings of the National Academy of Sciences, 113(28), pp.7900–7905.
3. Nichols, T.E. & Holmes, A.P., 2002. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum Brain Mapp, 15(1), pp.1–25.
4. Van Essen, D.C. et al., 2012. The Human Connectome Project: A data acquisition perspective. Neuroimage, 62(4), pp.2222–2231.
5. Fonov, V. et al., 2011. Unbiased average age-appropriate atlases for pediatric studies. Neuroimage, 54(1), pp.313–327.
Figures
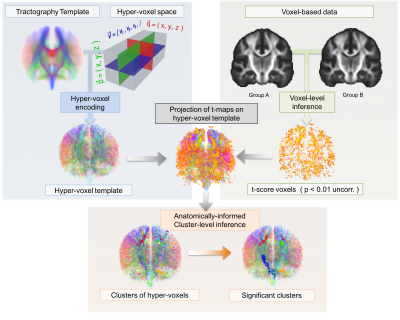

Figure-2 Anatomically-informed clustering criteria of hyper-voxels. Only three standard clusters of voxels C-1 to C-3 emerge in the shown example. In contrast, there are five different clusters of hyper-voxels: Clusters C-5 to C-9 are formed only by connected hyper-voxels. Cluster C-4 is formed both by connected hyper-voxels and by adjacent hyper-voxels. Note that as in the case of voxels, each hyper-voxel can only belong to one single cluster.