0616
Golden Angle Radial Reconstruction Using Partial Separability for High Spatiotemporal Resolution Liver Dynamic Contrast-Enhanced Imaging1Center for Biomedical Imaging Research, Tsinghua University, Beijing, China
Synopsis
Dynamic Contrast-Enhanced imaging is an important tool in diagnosing hepatic diseases. Improving spatiotemporal resolution is of great significance for clinical purpose. In this work we introduce the partial separability constraint to the reconstruction of stack-of-stars golden angle radial data. Both in-vivo and stimulated liver experiment were conducted and the proposed method (PS+S) showed better reconstruction quality compared to the existing methods without partial separability constraint.
Purpose
Stack-of-stars golden angle sampling has many advantages in hepatic dynamic imaging, like insensitivity to motion and uniform sampling pattern. Furthermore, its inherent sparsity character makes it an ideal trajectory for compressed sensing reconstruction [1]. In hepatic dynamic imaging, getting higher spatial image quality with less compromise in temporal dimension is crucial, because the relative enhancement after injection is an important clinical metric. Many dynamic GA reconstruction methods were proposed in recent years, among which GRASP [2] can achieve relatively high performance. However, in order to achieve high image quality, the time-zone sparsity penalty may smooth the intensity-time curve aggressively, deviating from the real pattern. By combining the PS constraint [3] with sparsity, the major temporal information will be preserved in a low-rank subspace extracted a priori. In this work, the proposed methods (PS+S) were tested on in-vivo and stimulated data, and outperformed GRASP on temporal and spatial dimension.Methods
The aim of proposed method is to minimize the following cost function.
$$\tilde{U_{s}}=arg min\left\{\parallel F\cdot S\cdot U_{s} \cdot V_{t}-m\parallel_2^2+\gamma_{t}\phi_{t}(U_{s}\cdot V_{t})+\gamma_{s}\phi_{s}(U_{s}\cdot V_{t})\right\}$$ where m is the sampled k-t-space signal arranged in Casorati matrix form, S represents the SENSE encoding map and F is the non-uniform Fourier transform. $$$\phi_{t}$$$ is the temporal sparsity constraint, and $$$\phi_{s}$$$ is the spatial penalty. To extract temporal projection more efficiently, the redundancy of sampling in the center of k-space is exploited. $$$V_{t}$$$ is estimated a priori by applying principal component analysis on the temporal dimension of image-series, which is reconstructed by zero-padded central k-space signal. The selection of $$$V_{t}$$$’s rank is a trade-off between preserving structural and dynamic information, which will be discussed in the latter section. The initial value of $$$V_{t}$$$ is obtained by multiplying the pseudo-inverse of $$$V_{t}$$$ with $$$d\prime$$$, which is the NUFFT solution to the inverse problem, to minimize the number of iterations. In all experiments, the number of conjugated gradient iterations are same for both methods.
Experiments: The test was conducted on two sets of data. In the simulated experiment, we generated the simulated series of images from an in-vivo acquired T1-weighted hepatic imaging. Aorta, portal vein, and liver tissue were selected as ROIs. From a pre-fitted equation described in [4, 5, 6], the AIF (arterial input function) curve, PIF (portal venous input function) curve and liver tissue curve were generated. In the in-vivo experiment, we scanned a healthy volunteer on a 3.0T Phillips scanner (Achieva, Philips Healthcare, Best, Netherlands) with 36-channel cardiac coils. The parameters are following: FOV=320×320×200$$$mm^{3}$$$, Flip Angle=20°, TR/TE= 3.60/1.44ms, in-plane resolution=1.25×1.25$$$mm^{2}$$$. 1280 radial projections were acquired with 256 readout points in each line. Gd-DTPA with concentration of 0.1mmol/kg was injected at 2 ml/s, and the acquisition started simultaneously.
Analysis Methods: Each frame was reconstructed by 21 spokes in both scenarios. Non-linear conjugated gradient method was used for the optimization. In simulation, the concentration curve were calculated and the parameter was fitted to the curve, in order to measure the fidelity. In in-vivo experiment, standard deviation of a small blank region without streaking artifacts was assumed to be background noise level and was used to calculate the SNR.
Results
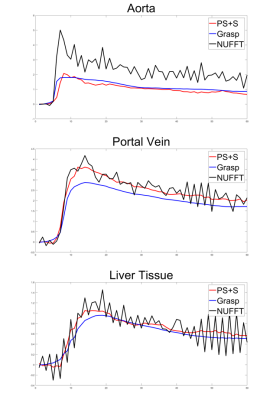
For the simulated data, the curves of reference image, GRASP image and PS+S image were showed in Fig. 1. PS+S curve fits reference better, especially for the AIF curve, which changes dramatically after the injection. RMSE is also compared (Table 1), and PS+S achieved higher quality in most items. In the in-vivo experiment, the blurring and streaking artifacts are suppressed (Fig. 2), and higher SNRs are achieved in three ROIs (aorta, portal vein and liver tissue) (Table 2). Moreover, the peaks of AIF and PIF are fitted closer by PS+S(Fig. 3).Discussion
Like in other low-rank decomposition methods, the selection of appropriate rank is central to the reconstruction. Lower rank can preserve main static structure on the cost of temporal resolution. In the experiment, we draw the relative enhancement curve of reconstructed image, and comparison with NUFFT curve can help to determine whether the rank is too low. For the temporal sparsity coefficient, PS+S needs smaller penalization than GRASP, so the temporal blurring is less. Since the low-rank decomposition has already guaranteed the image quality, the spatial sparsity penalty weight is set to a low level to prevent blurring.Conclusion
The PS+S method to reconstruct dynamic image from golden-angle radial trajectory was described and validated in this work. The proposed method shows better spatial quality with less loss of temporal information compared to GRASP. More advanced principle component extraction method could also be incorporated into this framework.Acknowledgements
No acknowledgement found.References
1. Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.
2. Feng, Li, et al. "Golden‐angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden‐angle radial sampling for fast and flexible dynamic volumetric MRI." Magnetic resonance in medicine 72.3 (2014): 707-717.
3. Zhao, Bo, et al. "Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints." IEEE transactions on medical imaging 31.9 (2012): 1809-1820.
4. Materne, R., et al. "Assessment of hepatic perfusion parameters with dynamic MRI." Magnetic resonance in medicine 47.1 (2002): 135-142.
5. Li, Xia, et al. "A novel AIF tracking method and comparison of DCE-MRI parameters using individual and population-based AIFs in human breast cancer." Physics in medicine and biology 56.17 (2011): 5753.
6. Materne, R., et al. "Non-invasive quantification of liver perfusion with dynamic computed tomography and a dual-input one-compartmental model." Clinical Science 99.6 (2000): 517-525.
Figures
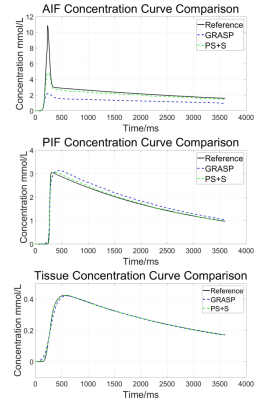
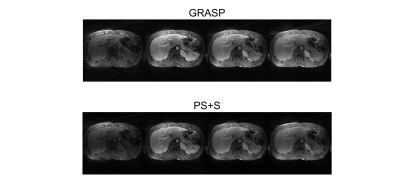

Table 1 RMSE comparison
for reference, GRASP and PS+S results.
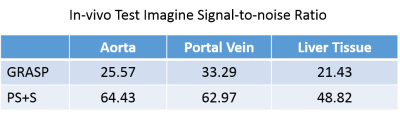
Table 2 The signal-to-noise ratio of in-vivo data. Standard deviation of a small blank region without obvious streaking artifacts is assumed to be background noise level.